Тема 4. Расчет балки на прочность и жесткость при изгибе.
Задача 4.Для заданных двух схем балок (рис. 4, табл. 5) требуется написать
выражения Q и M для каждого участка, построить эпюры Q и M, найти Mmax и подобрать (схема а) или б) – по выбору преподавателя):
а) для схемы а деревянную балку круглого поперечного сечения при [σ] = 8 МПа;
б) для схемы б – стальную балку двутаврового поперечного сечения при [σ] = 160 МПа.
Указание. При выборе двутавра можно использовать приложение 1.
Таблица 5
| Цифра шифра | Схема по рис. 4 | l1 | l2 | Расстояние в долях пролета | M, кН⋅м | P, кН | q, кН / м | ||
| м | a1 /a | a2 /a | a3 /a | ||||||
| 0 | I II III IV V VI VII VIII IX X | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | |||||||
| Буква шифра | е | д | е | г | д | е | г | д | е |
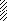 |
 |
 |
 |
а) q б) q Р 2Р
I
a1 M
a2a2 a1 a3
l1 = 10a l2 = 10a
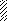 |
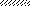 |
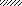 |
а) q б)q Р
M
II
a2 a1 a1 a3 a2
l1 = 10a l2 = 10a
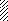 |
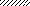 |
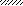 |
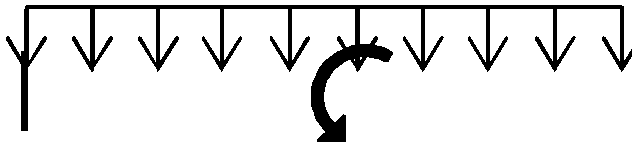
а) q б) q Р q
M
III
a1 a2 a3 a2 a1
l1 = 10a l2 = 10a
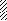 |
 |
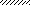 |
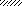 |
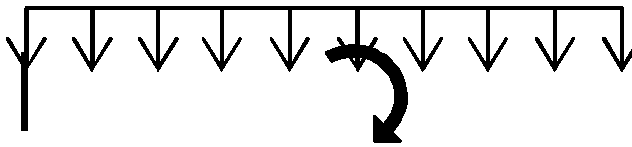
а) q б)q
IV
M
a3
a2 Р a3 a2
l1 = 10a l2 = 10a
Рис. 4
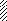 |
 |
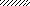 |
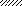 |
q q
V Р
M
a1
a3 a3 a2
l1 = 10a l2 = 10a
P
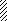 |
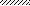 |
M
VI
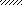 a1
a1
a2 a2 a1 a3
l1 = 10a l2 = 10a
а)
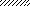 |
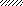 |
VII
M
a1 a2 a3 a2 a1
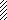 |
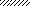 |
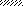 |
а) P q б)qq
M
VIII
a1 a2 a3 a2 a1
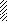 |
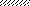 |
 |
 |
M
IX
a2
a1 a2 a3
l1 = 10a l2 = 10a
 |
 |
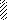 |
Q P q
X
M
a3 a3 P a3 a3 a2
l1 = 10a l2 = 10a
Рис. 4. Окончание
Задача 5.Для балки, изображенной на рис. 5, требуется:
1) найти изгибающий момент на левой опоре (в долях ql2);
2) построить эпюры Q и M;
3) построить эпюру прогибов, вычислив три ординаты в пролете и две – на консоли.
Данные взять из табл. 6.
Указание. Жесткость при изгибе принять постоянной EJx для всех участков балки.
Таблица 6
| Цифра шифра | Схема по рис. 5 | α | β | Цифра шифра | Схема по рис. 5 | α | β | |
| 5 | I II III IV V | 0,1 0,2 0,3 0,4 0,5 | 0,1 0,2 0,3 0,4 0,5 | VI VII VIII IX X | 0,6 0,7 0,8 0,9 1,0 | 0,6 0,7 0,8 0,9 1,0 | ||
| Буква шифра | е | г | д | Буква шифра | е | г | д |
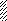 |
 |
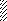 |
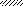 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
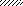 |
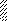 |
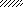 |
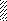 |
 |
 |
 |
P=αql
P=αql
II q VII q
q
VII
P=αql
q
P=αql
P=αql P=αql
q VIII P=αql q
III
P=αql
q P=αql
VIII
P=αql
P
P=αq
q P=αql q
IV IX
P=αql
P=αql P=αql P=αql
P=αql q q
V X
P=αql
l / 2 l / 2 β l l / 2 l / 2 β l
Рис. 5
Указания. Для ответа на первый вопрос нужно составить два уравнения:
1) уравнение статики в виде суммы моментов всех сил относительно правой опоры;
2) уравнение метода начальных параметров, учитывающее нулевой прогиб на правой опоре. Из этих двух уравнений можно найти реактивные момент и силу в заделке.
Для ответа на третий вопрос целесообразнее всего использовать метод начальных параметров, так как два начальных параметра (y0 и θ0) обращаются в ноль (при условии расположения начала координат в заделке), а два других (M0 и Q0) перед этим были найдены.
Тема 5. Расчёт статически неопределимой плоской рамы.
Задача 6. Требуется:
1) изобразить расчётную схему рамы в масштабе и с указанием всех размеров и нагрузок в числах;
2) установить степень статической неопределимости;
3) выбрать основную систему метода сил. Изобразить основную и эквивалентную системы;
4) записать каноническое уравнение метода сил;
5) построить единичную и грузовую эпюры;
6) вычислить коэффициент и свободный член канонического уравнения;
7) решить каноническое уравнение относительно неизвестных;
8) определить значения изгибающих моментов в характерных сечениях рамы и построить результирующую эпюру М;
9) выполнить деформационную проверку по эпюре М;
10) построить эпюры поперечных Q и продольных N сил;
11) выполнить статическую проверку расчёта рамы.
Данные взять из табл.7, схему рамы выбрать из рис. 6.
Таблица 7
| Цифра шифра | Схема из рис. 6 | ℓ, м | h, м | J 1 | J 2 | P, кН | q, кН/м |
| Буква шифра | д | в | г | д | в | е | г |
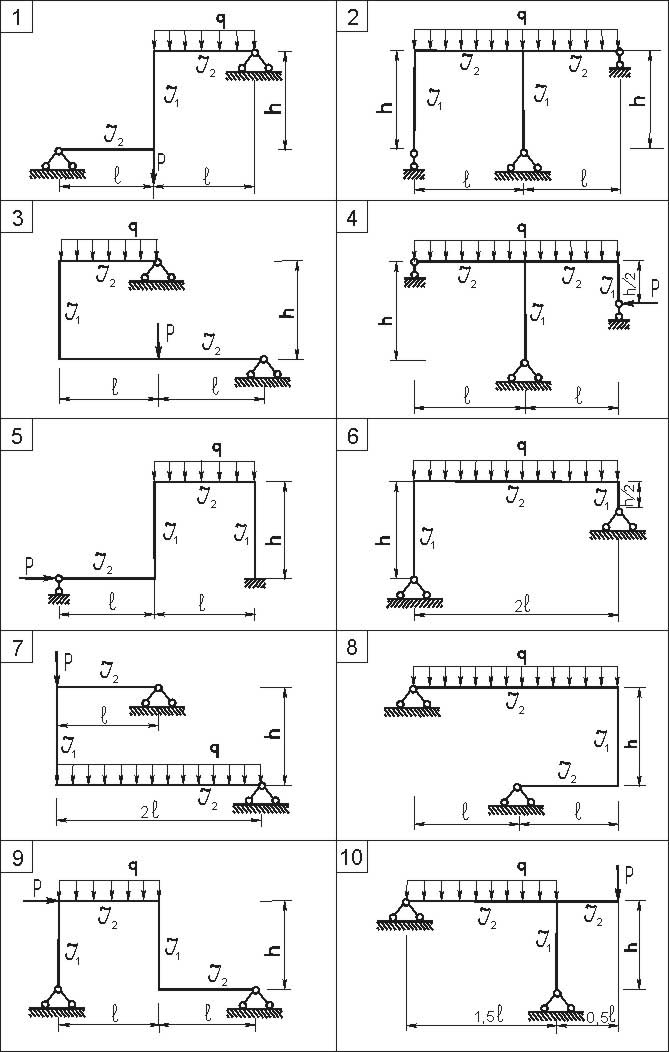
Рис. 6
