Тема 2. Расчет конструкций на прочность и жесткость при растяжении (сжатии).
Задача 2.Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням с помощью шарниров (рис. 2). Требуется:
1) найти усилия и напряжения в стержнях, выразив их через силу Q;
2) найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа;
3) принимая материал стержней идеально пластичным, найти предельную грузоподъемность системы Qт и допускаемую нагрузку Qдоп, если предел текучести σт = 240 МПа и запас прочности k = 1,5;
4) сравнить величины Qдоп, полученные при расчете по допускаемым напряжениям (см.
п.2) и допускаемым нагрузкам (см. п.3).
Данные взять из табл. 2.
Таблица 3
| Цифра шифра | Схема по рис. 2 | A, см2 | Расстояния, м | ||
| a | b | c | |||
| 0 | I II III IV V VI VII VIII IX X | 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 | 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | |
| Буква шифра | е | в | г | д | е |
 I II III
I II III
 |
 |
 |
 |
 |
 |
 |
 |
 A 2A 2A A
A 2A 2A A
 A 2A a с a b c
A 2A a с a b c
 |
a
c c
Q Q Q
IV V
 |
 |
 |
 A A
A A
 |
 |
 |
 2A b c 2A Q
2A b c 2A Q
Q
a b
VI VII VIII
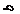
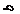
 |
 |
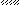 |
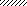 |
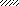 |
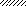 |
 |
| A |
с a b b c a b b a c
IX X
 |
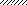 |
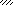 |
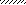 |
 |
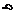 A 2A
A 2A  Q 2A A A Q
Q 2A A A Q
a c b c b a
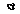 Рис.2
Рис.2
Указания. Для определения двух неизвестных усилий в стержнях следует совместно решить уравнение статики и уравнение совместности деформаций.
Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней напряжение может быть больше, чем в другом. При увеличении нагрузки напряжение в этом стержне достигнет предела текучести раньше, чем во втором. Для идеально пластичного материала дальнейший рост напряжений в этом стержне прекращается, и усилие растяжения в нем становится постоянным N1пред = σт⋅A1. При дальнейшем увеличении нагрузки достигается предел текучести и в другом стержне (N2пред = σт⋅A2). Подставив в уравнение статики предельные значения усилий в стержнях, найдем из него предельную грузоподъемность Qпр, а затем и допускаемую нагрузку Qдоп.
Тема 3. Расчет бруса на прочность и жесткость при кручении.
Задача 3.К стальному валу приложены три известных крутящих момента: M1, M2, M3 (рис. 3).
Требуется:
1) установить, при каком значении крутящего момента X угол закручивания правого концевого сечения вала равен нулю;
2) для найденного значения X построить эпюру крутящих моментов;
3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;
4) найти наибольший относительный угол закручивания (на 1 м длины).
Данные взять из табл. 4.
Таблица 4
| Цифра шифра | Схема по рис. 3 | Расстояния, м | Моменты, кН⋅м | [τ] МПа | ||||
| a | b | c | M1 | M2 | M3 | |||
| 1 2 3 4 5 6 7 8 9 | I II III IV V VI VII VIII IX X | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | |
| Буква шифра | е | г | д | б | в | д | е | в |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
I VI
M1 M2 M3 X M1 M2 M3 X
II VII
VII
M1 M2 M3 X
M1 M2 M3 X M1 M2 M3 X
III VIII
M1 M2 M3 X
VIII
M1 M2 M3 X
M1 M2 M3 X M1 M2 M3 X
IV IX
M1 M2 M3 X
M1 M2 M3 X M1 M2 M3 X
V X
M1 M2 M3 X
X
d b c e b c e d
a b c a
Рис. 3
