Математические задачи энергетики

Математические задачи энергетики

Курс лекций

Доц. Джура С.Г.

Донецк 2007.

Рекомендуемая Литература:

1. Веников В.А. и др. «Математические задачи энергетики».– М. Высшая школа, 1990. - 543 с.

2. Перхач В.С. «Математические задачи энергетики».– Львов: Высшая школа, 1985. - 464 с.

3. Бернас С., Цек З. «Математические модели элементов электроэнергети-ческих систем». - М.: Энергоиздат, 1982, - 312 с.

4. Курицкий Б.Я. Поиск оптимальных решений средствами Exel 7.0. – Спб.: BHV, 1997. – 384 с.

5. Тукенов А.А. Рынок электроэнергии: от монополии к конкуренции. – М.: Энергоатомиздат, 2005. – 416 с.

6. Метод. указания: № 190 (старый на рус.) и №555 (на укр.) - для лабораторных работ и № 836 (на рус.) и №636 (на укр.) для курсовой работы.

ВВЕДЕНИЕ

Система электроснабжения промышленного предприятия включает в себя:

· сети до 1000В и выше;

· трансформаторные и преобразовательные подстанции;

· распредустройства;

· устройства защиты и автоматики;

· вспомогательное оборудование.

Система электроснабжения промышленного предприятия (СЭПП) предназначена для передачи и распределения электроэнергии в необходимом количестве и нужного качества.

Единая энергосистема

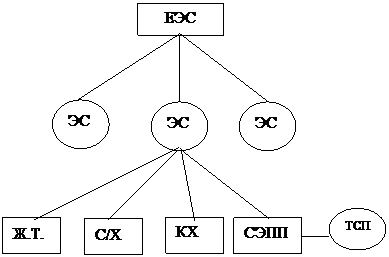Ж.Т. – железнодорожный транспорт;

С/Х – сельское хозяйство;

КХ – коммунальное хозяйство;

СЭПП – система электроснабжения промышленных предприятий;

ТСП – технологическая система предприятия

СЭПП является подсистемой энергосистемы и подсистемой технологической системы промышленного предприятия.

При проектировании и эксплуатации СЭПП решаются задачи анализа, синтеза и управления.

При анализе изучаются функции системы.

При синтезе изучаются структура системы, ее параметры и их определения.

При исследовании определяются координаты режима. Под координатами режима понимаются величины: токи, скорости, ускорения, потокосцепления, направления и т.д.

Связь между элементами систем может задаваться в виде зависимости. Параметры зависимости разделяются на линейные и нелинейные.

	Lд ЛИН

НЕЛИН

y

I

Для различных объектов составляем уравнения состояния. В эти уравнения кроме координат режима входят ЭДС, источник тока электромагнитные моменты.

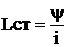(статическая индуктивность)

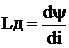(динамическая индуктивность)

При анализе установившегося режима решаем систему линейных и нелинейных алгебраических уравнений

При анализе переходных процессов решаем систему линейных и нелинейных дифференциальных уравнений.

В системах могут быть небольшие и глубокие кратковременные возмущения.

В 1-м случае исследуем статическую устойчивость, а во 2-м динамическую устойчивость.

При анализе исследуем электромагнитные и электромеханические переходные процессы.

ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Наиболее эффективным для описания процессов в электроэнергетике является матрично-векторный аппарат. Он приспособлен для использования ЭВМ и позволит автоматически регулировать уравнения состояния.

Для формализации методов расчета применяется геометрическая теория электрических цепей. Геометрические свойства электрической цепи определяется ее схемой.

Е

R I

двухполюсник

Совокупность двухполюсников образует электрическую схему.

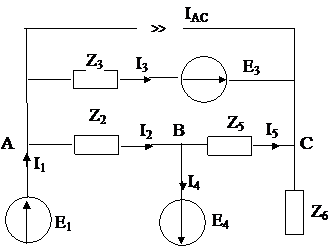
Геометрическая схема двухполюсников – направленный отрезок.

			I6

		Z4
		Z1

		C
		D

Геометрическая схема цепи – это совокупность направленных отрезков, соединенных тождественно электрической схеме.

Число ветвей – р

Число узлов – q

Число независимых узлов - q-1

Число независимых контуров - n

n=p-(q-1)=p-q+1

Ток к цепи обозначаем через “+” (плюс).

Ток из цепи обозначаем через “-“ (минус).

Положительное направление контура – направление правого вращения (по часовой стрелке).

МАТРИЦА СОЕДИНЕНИЙ

1 2 3 4 5 6

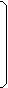1 -1 -1 0 0 0 А

П₀ = 0 1 0 -1 -1 0 В

0 0 1 0 1 1 С

-1 0 0 1 0 -1 D

Элементы матрицы обозначим через П_ij

Если j-я ветвь входит в узел то «+1», если выходит из узла – «-1».

Если не принадлежит узлу – «0».

В этой матрице имеется избыточная информация. Один узел можно отбросить, например узел D. Отброшенный узел называется базисным или узлом баланса.

Матрице соединений отвечает только одна электрическая схема.

Отброшенная строка может быть легко восстановлена, если учесть, что в каждом столбце имеется +1 и –1.

МАТРИЦА КОНТУРОВ

I II III

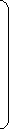
1 0 0 1

1 -1 0 2

Г = 0 1 0 3

1 0 -1 4

0 -1 1 5

0 0 1 6

Элемент матрицы обозначим через Г_ij

Если i-я ветвь совпадает по направлению с j-м контуром, то “+1”, если не совпадает, то “-1”. Если i-я ветвь не принадлежит j-м контуру, то “0”.

Матрица контуров может отвечать нескольким электрическим схемам.

Справедливо соотношение:

П ^. Г = 0

Разобьем матрицу соединений и матрицу контуров на подматрицы.

П =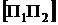

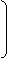
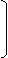Г₁ Г₁

Г = ,

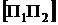
Г₂ Г₂

П₁^.Г₁ + П₂^.Г₂ = 0

Выберем Г₁ = 1

Тогда: П₁ + П₂Г₂ = 0

Г₂ = -П₂^–1 П₁

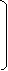
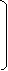
Г₁ 1

Г = =

Г₂ -П₂^-1П₁

Следовательно, матрицу контуров можно вычислить по матрице соединений.

ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Необходимо составить:

Матрицу сопротивлений (Z)

Матрицу проводимости (Y)

Матрицу-столбец ЭДС: матрицу-столбец источников тока:

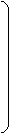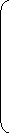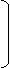
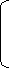Е₁

_® О _® -I_AC A

Е = Е₃ I = O B

Е₄ I_AC C

О

Векторы напряжений и токов:

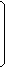
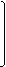_® U_{1 ®} I₁

U = U₂ I = I₂

U₆ I₆

Многомерный вектор мощностей:

_{® ® ® * * *}

S = I U = (I₁U₁, I₂U₂,...,I₆U₆) = (S₁, S₂,...,S₆)

Многомерный вектор мощностей источников ЭДС:

_{® ® ® * * *}

S_E = I E = (I₁E₁, I₂E₂,..., I₆E₆) = (S_1E, S_2E,…,S_6E)

Многомерный вектор источников тока:

_{® ® ® * *}

S_I = IU_AC = (-I_ACU_AC, 0, I_AC,U_AC)

ЗАКОН ОМА

U₁ = E₁ - z₁₁I₁ - z₁₂I₂ - …- z_1nI_n

U₂ = E₂ - z₂₁I₁ – z₂₂I₂ -…- z_2nI_n

…..

U_n = E_n – z_n1I₁ – z_n2I₂ - …- z_nnI_n

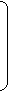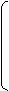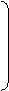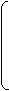U₁ E₁ z₁₁ z₁₂…z_1n I₁

U₂ = E₂ - z₂₁ z₂₂…z_2n I₂

… … ……………. …

U_n E_n z_n1 z_n2…z_nn I_n

® ® ® U = E – z I

З-н Ома

для эл. схемы

Й ЗАКОН КИРХГОФА

åI_c = 0

_® I – й закон Кирхгофа

ПI = 0 при отсутствии источника

тока

_{® ®}

ПI + I = 0 1- й закон Кирхгофа при

наличии источников тока

Й ЗАКОН КИРХГОФА

åU_c = 0

_®

Г_tU = 0

Непосредственно на основе законов Ома и Кирхгофа расчет электрических цепей не производится.

При наличии р – ветвей конечная система уравнений будет иметь р неизвестных токов и р неизвестных напряжений. Общее число неизвестных 2р.

МЕТОД ЗАКОНОВ КИРХГОФА

_{® ®}

ПI + I = 0 p > q –1

_®

Г_tU = 0

_{® ® ®}

U = E – z I

Во 2-е уравнение Кирхгофа подставим выражение для напряжения по закону Ома

_{® ®}

Г_t (E – z I) = 0

_{® ®}

Г_t E - Г_t z I = 0

_{® ®}

Г_t E = Г_t z I

Полученное уравнение является 2-м уравнением Кирхгофа, записанным в системе токов. Совместно с 1-м законом Кирхгофа при наличии источника тока

П _® -I

^. I = уравнение для расчета токов

Г_tZ Г_tE

_®

Г_tU = 0 n < p Расчет напряжений

Непосредственно этим уравнением нельзя воспользоваться для нахождения напряжений. Уравнений будет меньше чем неизвестных.

Нужны дополнительные уравнения.

Для их нахождения воспользуемся Законом ома для участка цепи:

_{® ® ®}

U = E – z I

Отсюда

I = Y (E – U)

_{® ® ®}

I = z^-1(E – U)

_{® ® ®} Закон Ома

Первое уравнение Кирхгофа подставляем в выражение для тока по закону Ома: _{® ®}

П I + I = 0

Получим:

_{® ® ®}

П Y (E – U) + I = 0

_{® ® ®}

П YE – П Y U + I = 0

_{® ® ®}

ПYU = ПYE+I

Полученное уравнение является 1-м законом Кирхгофа, записанным в системе напряжений.

Таких уравнений столько, сколько независимых узлов.

В итоге для напряжения имеем следующую систему уравнений:

_®

Г_t U = 0 (n)

_{® ® ®}

П Y U = П Y E + I

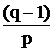уравнений

Запишем эти уравнения в матричной форме:

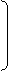
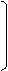
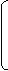Г_{t ®} 0

^. U = _{® ®}

ПY ПYE + I

МЕТОД НЕЗАВИСИМЫХ ТОКОВ

_{® ®}

П I = -I

Делим вектор тока на две составляющие:

_®

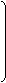
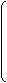_® I_I

I = _®

I_II

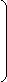_® I₁

I_I = I₂ столько составляющих, сколько

... независимых токов

I_n

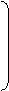
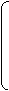_® I_n+1

I_II = I_n+2

… остальные токи во II-м векторе

I_p

Токи, входящие в I-й вектор тока будем считать независимыми токами, если через них можно выразить все остальные токи электрической схемы.

Соответствующим образом матрицу соединения разбиваем на 2 подматрицы:

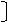
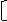
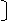
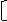П = П₁ П_{2 .}

в итоге получим уравнение:

_®

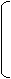
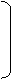I_{I ®}

П₁ П₂ ^. _® = -I

I_II

Запишем это уравнение в развернутом виде:

_{® ® ®}

П₁I_I + П₂I_II = -I

_{® ® ®}

I_II = -П₂^-1П_II_I – П₂^-1I

_{® ®}

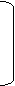
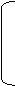
_® I_I I_I 1 _® 0 _®

I = _® = _{® ®} = I_I - I

I_II -П₂^-1П_II_I – П₂^-1I -П₂^-1П_I П₂^-1

Все токи схемы можно определить, зная независимые токи.

Для нахождения независимых токов воспользуемся II-м законом Кирхгофа, записанным в системе токов:

_{® ®}

Г_t z I = Г_t E

_{® ® ®}

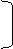
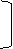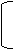
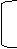Г_t z 1 I_I = Г_t E + Г_tz 0 I

-П₂^-1 П₁ П₂^-1

уравнение независимых токов

Таких уравнений столько, сколько независимых контуров.

Введем обозначения:

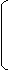
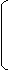1

Б₁ =

-П₂^-1П₁

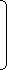
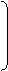0

К₁ = Г_tz

П₂^-1

Б₁ - матрица преобразования независимых токов.

К₁ - матрица преобразования источников тока в соответствии имеющихся

эквивалентов ЭДС.

_{® ® ®}

Г_t z Б₁ I_I = Г_tE + К₁I

z₁ = Г_t z Б₁ – матрица сопротивлений по методу независимых токов.

_{® ® ®}

z₁I_I = Г_tE + К₁I

_®

Обозначим: Г_t Е – вектор контурных ЭДС;

_{® ®}

Г_tЕ = Е_кк – вектор контуров ЭДС;

_{® ®}

К₁I = Е_к – вектор эквивалентных контуров ЭДС.

_{® ® ®}

z₁I_I = E_кк + Е_к

_{® ®}

z₁I_I = E_å

Пример:

Последовательность ветвей в матрицах и

векторах должна соответствовать после-

II

довательности токов в векторе!

В

C

D

E

III

_®

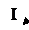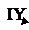Знак ЭДС в векторе Е: "+" – если совпада-

ет с выбранным направлением тока в

ветви

"-" – если не совпадает

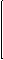
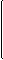1 0 _®

Г_t z I_I = Г_tE + Г_t z I

-П₂^-1П₁ П₂^-1

n = p – q + 1 = 8 – 5 + 1 = 4, (p – ветвей, q- узлов).

4 независимых тока (выбираем I₁, I₂, I₃, I₄)

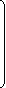
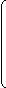I₁

_® I₂

I_I = I₃

I₄

При выборе независимых токов ни один узел электрической схемы не должен быть полностью заполненным. В противном случае П₂ будет особенной и задача не будет иметь решений.

Составляем матрицу соединений:

1 2 3 4 5 6 7 8

-1 0 0 1 0 0 1 0 А A

П = П₁ П₂ = 1 -1 0 0 -1 0 0 0 В B

0 1- 1 0 0 0 0 -1 D C

0 0 1 -1 1 -1 0 0 C D

П₁ П₂

1 2 3 4 5 6 7 8

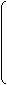1 1 0 0 0 0 1 1 I

0 -1 -1 0 1 0 0 0 II

Г_t = 0 0 1 0 0 1 0 -1 III

0 0 0 1 0 -1 –1 0 IY

При нахождении Г_t z вместо 1 ставим "z₁", вместо -1 - "-z₁"

в первом столбце, и т.д. во всех столбцах.

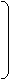
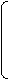z₁ z₂ 0 0 0 0 z₇ z₈

Г_t z= 0 -z₂ -z₃ 0 z₅ 0 0 0

0 0 z₃ 0 0 z₆ 0 -z₈

0 0 0 z₄ 0 -z₆ -z₇ 0

Аналогично Г_t E.

Матрица Б₁ может быть получена без каких либо вычислений

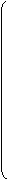
I₁ I₂ I₃ I₄

1 0 0 0 I₁

1 0 1 0 0 I₂

Б₁ = = 0 0 1 0 I₃

-П₂^-1 П₁ 0 0 0 1 I₄

1 -1 0 0 I₅ = I₁ – I₂

1 -1 1 1 I₆ = I₃ + I₅ –I₄ Þ

1 0 0 -1 I₇ = I₁ – I₄

0 1 -1 0 I₈ = I₂ – I₃

Токи с 5-го по 8-ой необходимо выразить через независимые токи, полученные при независимых токах коэффициенты необходимо расставить на соответствующие места матрицы.

Þ I₆ = I₁ – I₂ + I₃ –I₄

Таким образом, в итоге получим систему из 4-х уравнений с четырьмя неизвестными токами. Решая эту систему, находим независимые токи.

Все токи электрической схемы можно найти так:

_{® ®}

I = Б₁ I_I если нет источника тока

или есть источник тока:

_{® ®} 0 _®

I = Б₁ I_I – П₂^-1 I

МЕТОД КОНТУРНЫХ ТОКОВ

Недостаток метода независимых токов заключается в том, что в общем случае матрица z₁ является несимметричной.

Ее вычисление затруднено, т.к. необходимо найти произведение трех матриц:

z₁ = Г_t^.z^.Б₁

Эту матрицу нельзя получить непосредственно из электрической схемы. Вычисления значительно упрощаются при выполнении следующего условия:

Б₁ =Г

В этом случае матрица z₁ является симметричной и может быть записана непосредственно из электрической схемы.

Матрица сопротивления, при этом, называется матрицей контурных сопротивлений:

z_к = Г_t z Г

А вектор токов называется вектором контурных токов

_{® ®}

I_кн = I_I

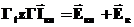
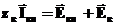уравнение контурных

токов

Пример

расчет методом

контурных токов

IY

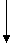
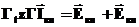
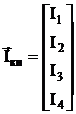
Матрица контурных сопротивлений имеет вид

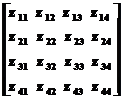= z_кн = Г_t z Г

По главной диагонали располагаются собственные сопротивления. Вне главной диагонали – взаимные.

Собственные сопротивления равны сумме сопротивлений ветвей, входящих в рассматриваемый контур.

z₁₁-собственное сопротивление I-го контура:

z₁₁=z₁+z₂+z₇+z₈

z₂₂=z₂+z₃+z₅

и т.д.

Взаимные сопротивления равны с обратным знаком сопротивлениям ветвей, смежных рассматриваемым контуром.

z₁₂=-z₂; z₂₁=-z₂

В итоге получим систему уравнений с четырьмя неизвестными контурными токами.

Решая ее находим контурные токи и по ним все остальные токи

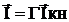если нет источников тока

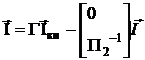
Метод узловых напряжений

Это частный метод. Он получен из метода независимых напряжений.

Недостаток метода независимых напряжений в том, что в общем случае матрица проводимостей У₁ является несимметричной. Для ее нахождения необходимо найти производную трех матриц.

Y₁ = ПYБ₂

Расчеты упрощаются при выполнении условия

Б₂ = П_t

Тогда получим матрицу узловых проводимостей

Y_у = ПYП_t

А вектору независимых напряжений будет соответствовать вектор узловых напряжений

_→

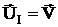
Матрица У_у является симметричной и может быть легко получена непосредственно из электрической схемы.

В итоге имеем уравнение _{→ → →}

ПYП_t V = ПYЕ + I

_{→ → →}

Y_yV = ПYЕ + I

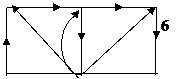
Пример:

q –1 =3 (независимые узлы)

V1

V3

V2

D

C

B

A

( независимые напряжения)

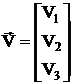
Y₁₁ Y₁₂ Y₁₃

Y_у = Y₂₁ Y₂₂ Y₂₃

Y₃₁ Y₃₂ Y₃₃

Для нахождения проводимостей, расположенных по главной диагонали необходимо сложить проводимости ветвей, входящих в рассматриваемый узел.

Y₁₁ = Y₁ + Y₂ + Y₃

Y₂₂ = Y₂ + Y₄ + Y₅

Y₃₃ = Y₃ + Y₅ + Y₆

Для нахождения проводимостей, которые находятся вне главной диагонали необходимо их приравнять с обратным знаком к проводимостям ветвей, соединяющих рассматриваемые узлы.

Y₁₂ = - Y₂; Y₂₁ = - Y₂

и т.д.

В итоге получим систему из 3-х уравнений с тремя неизвестными узловыми напряжениями. Определив узловые напряжения, можно найти все напряжения ветвей электрической схемы:

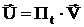
К расчету электрических токов:

Вектор тока можно найти, если известны контурные токи.

Из метода контурных токов:

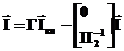
А контурные токи находим из контурных уравнений

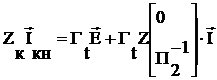
Отсюда найдем 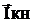- вектор контурных токов

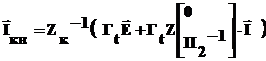
z_к = Г_t z Г

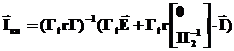
Подставляем в первую формулу:

Перемножим:

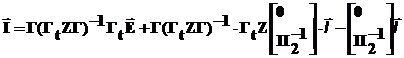
Введем обозначения

у_Е = Г(Г_tzГ)^-1Г_t - матрица входных и взаимных проводимостей

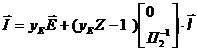
Перед источниками тока стоит коэффициент распределения

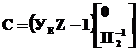
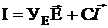
Полученное выражение непосредственно из электрической схемы получить нельзя. Для его получения необходимо громоздкие математические выражения.

К расчету напряжений ветвей электрической схемы:

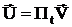из метода условных напряжений

Запишем узловое уравнение:

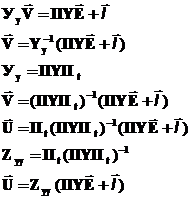
Непосредственно из электрической схемы выражение для напряжений получить нельзя. Для его получения необходимо провести много математических вычислений.

В электрических расчетах применяется матрица узловых сопротивлений

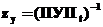
Случайные величины

Теория вероятности – это наука, изучающая закономерности случайных явлений. Невозможность учесть причины якобы случайных явлений (кз) приводит к необходимости использовать теорию вероятностей.

Случайное событие – это событие, которое в результате опыта может произойти или не произойти.

Достоверное событие – это событие, которое произойдет обязательно.

Невозможное событие – это событие, которое не может произойти.

Вероятность – численная степень возможности появления случайного события в данном опыте.

Р(А) – вероятность А

Р(А) = 1 достоверное событие

Р(А) = 0 невозможное событие

0 £ Р(В) £ 1

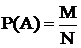
М – благоприятные случаи появления события А;

N – общее число случаев; (Это классическое определение вероятности)

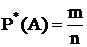- статистическое определение вероятности.

n – количество проведенных опытов

m – количество опытов в которых произошло событие А

Несколько событий называются несовместными, если никакие хотя бы 2 из них не могут произойти одновременно. В противном случае события – совместные.

Равновозможные события – это события, вероятность появления которых можно считать одинаковой.

Несколько событий, одно из которых наверняка произойдет образуют полную группу событий, причем эти события