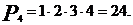Вероятность. Теоремы сложения и умножения вероятностей

Лекция № 7

Вероятность. Теоремы сложения и умножения вероятностей

Элементы комбинаторики

Группы, составленные из каких-либо элементов, называются соединениями.

Различают три вида основных соединений: размещения, перестановки и сочетания.

Задачи, в которых производится подсчёт возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.

Размещения

Размещениями из n элементов по m элементам называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.

Число размещений из n по m элементам обозначается символом 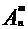и вычисляется по формуле:

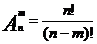(1)

Перестановки

Перестановками из n элементов называются такие соединения, которые отличаются друг от друга лишь порядком следования элементов.

Число перестановок обозначают символом P_n.

Перестановки представляют собой частный случай размещения и вычисляются по формуле:

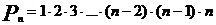(2)

Сочетания

Сочетаниями из n элементов по m называются такие соединения, каждое из которых содержит n элементов, взятых из данных m элементов, и отличается от другого хотя бы одним элементом, обозначается 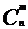и вычисляется о формуле:

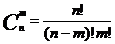(3)

Пример 1.1.Вычислить:

1) ;

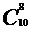2) Р₄.

Решение.

Применяем формулы (2) и (3):

1)

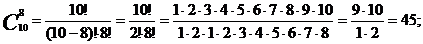
2)

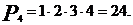
Теоремы сложения и умножения вероятностей

Теорема сложения

Вероятность наступления одного из нескольких несовместных событий равна сумме вероятностей этих событий.

В случае двух несовместных событий А и В имеем:

Р(А+В) = Р(А) + Р(В) (7)

Событие, противоположное событию А обозначают 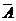. Объединение событий А и 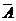даёт событие достоверное, а поскольку события А и 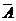несовместны, то

Р(А) +Р( 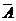) = 1 (8)

Вероятность события А, вычисленная в предположении, что событие В наступило, называется условной вероятностью события А и обозначается символом Р_В(А).

Если события А и В независимые, то Р(В) = Р_А(В).

События А, В, С, … называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой комбинации их и в любом числе.

Теорема умножения

Вероятность того, что произойдут события и А, и В, и С, … равна произведению их вероятностей, вычисленных в предположении, что все предшествующие каждому из них события имели место, т. е.

Р(АВ) = Р(А)Р_А(В)(9)

Запись Р_А(В) обозначает вероятность события В в предположении, что событие А уже имело место.

Если события А, В, С, … независимы в совокупности, то вероятность того, что произойдут все они, равна произведению их вероятностей:

Р(АВС) = Р(А)Р(В)Р(С) (10)

Пример 3.1.В мешке лежат шары: 10 белых, 15 чёрных, 20 голубых и 25 красных. Вынули один шар. Найти вероятность того, что вынутый шар окажется белым? чёрным? И ещё: белый или чёрный?

Решение.

Число всех возможных испытаний n = 10 + 15 + 20 + 25 = 70;

Вероятность Р(б) = 10/70 = 1/7, Р(ч) = 15/70 = 3/14.

Применяем теорему сложения вероятностей:

Р(б + ч) = Р(б) + Р(ч) = 1/7 + 3/14 = 5/14.

Примечание: заглавные буквы в скобках соответственно обозначают цвет каждого шара согласно условию задачи.

Пример 3.2В первом ящике два белых и десять чёрных шаров. Во втором ящике восемь белых и четыре чёрных шара. Из каждого ящика вынули по шару. Определить вероятность того, что оба шара окажутся белыми.

Решение.

Событие А – появление белого шара из первого ящика. Событие В – появление белого шара из второго ящика. События А и В – независимые.

Вероятности Р(А) = 2/12 = 1/6, Р(В) = 8/12 = 2/3.

Применяем теорему умножения вероятностей:

Р(АВ) = Р(А)Р(В) = 2/18 = 1/9.

Вопросы для повторения

1 Что называется факториалом?

2 Перечислите основные задачи комбинаторики.

3 Что называется перестановками?

4 Что называется перемещениями?

5 Что называется сочетаниями?

6 Какие события называются достоверными?

7 Какие события называются несовместными?

8 Что называется вероятностью события?

9 Что называется условной вероятностью?

10 Сформулируйте теоремы сложения и умножения вероятностей.

11 пр.Размещением из п элементов по к ( к ≤ п) называется любое множество, состоящее из к элементов, взятых в определенном порядке из данных п элементов.

Таким образом, два размещения из п элементов по к считаются различными, если они различаются самими элементами или порядком их расположения Число размещений из пэлементов по к обозначают А_п^к и вычисляют по формуле

А_п^к =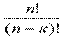

Если размещения из п элементов по п отличаются друг от друга только порядком элементов, то они представляют собой перестановки из п элементов

Пример1. Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета

Решение: Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо набором предметов, либо порядком их следования. Значит, в этом примере речь идет о размещениях из 9 элементов по 4. Имеем

А₉⁴ = 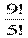= 6 ∙ 7 ∙ 8 ∙ 9 = 3024

Расписание можно составить 3024 способами

Пример2. Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0,1,2,3,4,5,6 ?

Решение Если среди семи цифр нет нуля, то число трехзначных чисел ( без повторения цифр), которые можно составить из этих цифр, равно числу размещений

22

из 7 элементов по 3. Однако среди данных цифр есть цифра 0, с которой не может начинаться трехзначное число. Поэтом из размещений из 7 элементов по3 надо исключить те, у которых первым элементом является 0. Их число равно числу размещений их 6 элементов по 2. =

Значит искомое число трехзначных чисел равно

А₇³ - А₆² = 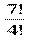- 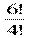= 5 ∙ 6 ∙ 7 - 5 ∙ 6 = 180.

3. Закрепление полученных знаний в процессе решения задач

№754. Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?

Решение. Число способов равно А₄³= 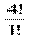= 1∙ 2 ∙ 3 ∙ 4 = 24

№755. Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?

Решение. Т.к.любой из участников может быть как секретарем , так и председателем, то число способов их избрания равно

А₃₀² = 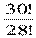= = 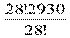29 ∙ 30 = 870

№762 Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр: а) 1,3,5,7,9. б) 0,2,4,6,8?

Решение а) А₅⁴= 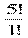= 1∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120

б) ) А₅⁴- А₄³= 5! – 4! = 120 – 24= 96

Домашнее задание № 756, №757, № 758, №759.

6урок Тема: « Сочетания»

Цель: Дать понятие о сочетаниях, познакомить с формулой для вычисления сочетаний, научить применять эту формулу для подсчета числа сочетаний.

1 Проверка домашнего задания.

№ 756. На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?

23

Решение: А₇⁴= 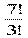= 4 ∙ 5 ∙ 6 ∙ 7 = 20 ∙ 42 = 840 способов

№757 Сколькими способами тренер может определить, кто из 12 спортсменок, готовых к участию в эстафете 4х100м, побежит на первом, втором, третьем и четвертом этапах?

Решение: А₁₂⁴= 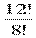= 9 ∙ 10 ∙ 11 ∙12 = 90 ∙132 = 11 880

№ 758. В круговой диаграмме круг разбит на 5 секторов. Секторы решили закрасить разными красками, взятыми из набора, содержащего 10 красок. Сколькими способами это можно сделать?

Решение: А₁₀⁵= 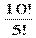= 6 ∙ 7 ∙ 8 ∙ 9∙ 10 = 30 240

№759. Сколькими способами 6 студентов, сдающих экзамен, могут занять места в аудитории, в которой 20 одноместных столов?

Решение: А₂₀⁶= 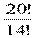= 15∙ 16 ∙17∙ 18∙19 ∙20 = 27 907 200

Организовать проверку домашнего задания можно разными способами: устно проверить решение домашних упражнений, решения некоторых из них записать на доске, а пока идет запись решений провести опрос уч-ся по вопросам:

1. Что означает запись п!

2.Что называется перестановкой из п элементов?

3.По какой формуле считают число перестановок?

4. Что называют размещением из п элементов по к?

5. По какой формуле считают число размещений из п элементов по к?

2 Объяснение нового материала

Пусть имеются 5 гвоздик разного цвета. Обозначим их буквами а, в, с, д, е. Требуется составить букет из трех гвоздик. Выясним, какие букеты могут быть составлены.

Если в букет входит гвоздика а , то можно составить такие букеты:

авс, авд, аве, асд, асе, аде.

Если в букет не входит гвоздика а , но входит гвоздика в , то можно получить такие букеты:

всд, все, вде.

Наконец, если в букет не входит ни гвоздика а, ни гвоздика в, то возможен только один вариант составления букета:

сде.

24

Мы указали все возможные способы составления букетов, в которых по – разному сочетаются три гвоздики из 5. Говорят, что мы составили все возможные сочетания из 5 элементов по 3, мы нашли, что С₅³= 10.

Выведем формулу числа сочетаний из п элементов по к, где к ≤ п.

Выясним сначала , как С₅³ выражается через А₅³ и Р₃. Мы нашли , что их 5 элементов можно составить следующие сочетания по 3 элемента :

авс, авд, аве, асд, асе, аде, всд, все, вде, сде.

В каждом сочетании выполним все перестановки. Число перестановок из 3 элементов равно Р₃. В результате получим все возможные комбинации из 5 элементов по 3, которые различаится либо самими элементами , либо порядком элементов, т.е. все размещения из 5 элементов по 3. Всего мы получим А₅³ размещений.

Значит , С₅³∙ Р₃= А₅³, отсюда С₅³= А₅³: Р₃

Рассуждая в общем случае получим С_п^к= А_п^к : Р_{к ,}

Пользуясь тем, что А_п^к = 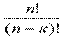, где к ≤ п., получим С_п^к= .

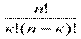Это формула для вычисления числа сочетаний из п элементов по к при любом

к ≤ п.

Пример1. Из набора, состоящего из 15 красок, надо выбрать3 краски для окрашивания шкатулки. Сколькими способами можно сделать этот выбор?

Решение : Каждый выбор трех красок отличается от другого хотя бы одной краской. Значит , здесь речь идет о сочетаниях из 15 элементов по 3

С₁₅³= 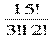= (13∙ 14∙15 ) : (1∙ 2 ∙ 3 ) = 455

Приме2 В классе учатся 12 мальчиков и 10 девочек. Для уборки территории около школы требуется выделить трех мальчиков и двух девочек. Сколькими способами можно сделать этот выбор?

Решение: Выбрать 3 мальчиков из 12 можно С₁₂³, а двух девочек из 10 можно выбрать С₁₀². Т. к. при каждом выборе мальчиков можно С₁₀²способами выбрать девочек, то сделать выбор учащихся, о котором говориться в задаче можно

С₁₂³∙ С₁₀²= 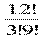∙ 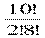= 220 ∙ 45 = 9900

3) Закрепление нового материала, в процессе решения задач

25

Задача

У Саши в домашней библиотеке есть 8 исторических романов. Петя хочет взять у него 2 любых романа. Сколькими способами можно сделать этот выбор?

Решение: С₈² = 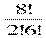= (7 ∙ 8) : ( 1∙ 2) = 56 : 2 = 28

№779 а

В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира команду из 4 человек?

Решение: С₁₆⁴ = 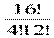= (13∙ 14∙15 ∙16 ) : (1∙ 2 ∙ 3 ∙ 4) = 13 ∙ 7 ∙5∙ 4 = 91 ∙20 = 1820

№774 Бригада, занимающаяся ремонтом школы, состоит из 12 маляров и 5 плотников. Из них для ремонта спротзала надо выделить 4 маляров и 2 плотников. Сколькими способами можно это сделать?

С₁₂⁴ ∙ С₅² = 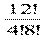∙ 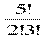= 495 ∙ 10 = 4950

Домашняя работа №768, №769, № 770, № 775

7урок Тема: « Решение задач на применение формул для подсчета числа перемещений, размещений, сочетаний»

Цель: Закрепление знаний учащихся. Формирование навыков решения простейших комбинаторных задач

1 Проверка домашнего задания

№768 В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?

Решение: С₇² = 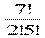= (6∙ 7) : 2 = 21

№769 В магазине « Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

Решение: С₈³ = 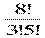= (6 ∙ 7 ∙ 8) : (1∙ 2 ∙ 3 ) = 56

26

№770 Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: С₁₀⁶ = 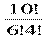= (7 ∙ 8 ∙ 9∙ 10) : (1∙ 2 ∙ 3 ∙ 4) = 210

№775 В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала?

Решение: С₁₀³ ∙ С₄² = 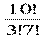∙ 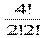= 120 ∙ 6 = 720

Вопросы классу

1.Что называется перестановкой из п элементов?

2.По какой формуле считают число перестановок?

3. Что называют размещением из п элементов по к?

4. По какой формуле считают число размещений из п элементов по к?

5. Что называют сочетанием из п элементов по к?

6. По какой формуле считают число сочетаний из п элементов по к?

Задачи для совместного решения

При решении каждой задачи вначале идет обсуждение: какая из трех изученных формул поможет получить ответ и почему

1. Сколько четырехзначных чисел можно составить из цифр 4,6,8,9, при условии , что все цифры разные ?

2. Из 15 человек в группе студентов надо выбрать старосту и его заместителя. Сколькими способами это можно сделать?

3. Из 10 лучших учащихся школы два человека надо послать на слет лидеров.

Сколькими способами это можно сделать?

Замечание : В задаче №3 не имеет значения кого выбрать: любых 2 человек из 10, поэтому здесь работает формула для подсчета числа сочетаний.

В задаче №2 выбирают упорядоченную пару ,т.к. в выбранной паре ,если фамилии поменять местами это будет уже другой выбор, поэтому здесь работает формула для подсчета числа размещений

Ответы к задачам для совместного решения:

№1 24 числа . №2 210 способов. №3 45 способов

Задачи для совместного обсуждения и самостоятельных вычислений

№1Встретились 6 друзей и каждый пожал руку каждому своему другу. Сколько было рукопожатий?

(Можно посчитать число сочетаний из 6 по 2)

27

№2 Сколькими способами можно составить расписание для учащихся 1класса на один день , если у них 7 предметов, и в этот день должно быть 4 урока?

( Число размещений из 7 по 4 )

№3 В семье 6 человек, а за столом в кухне 6 стульев. Было решено каждый вечер перед ужином рассаживаться на эти 6 стульев по- новому. Сколько дней члены семьи смогут делать это без повторений.

(Надо посчитать число перестановок в множестве с 6 элементами)

№4 К хозяину дома пришли гости А,В,С,Д. За круглым столом – пять разных стульев. Сколько существует способов рассаживания?

( В гости пришли 4 человека + хозяин = 5 человек рассаживаются на 5 стульях, надо посчитать число перестановок)

5. В книжке раскраске нарисованы непересекающиеся треугольник, квадрат и круг. Каждую фигуру надо раскрасить в один из цветов радуги, разные фигуры в разные цвета. Сколько существует способов раскрашивания?

( Посчитайте число размещений из 7 по 3 )

№6 В классе 10 мальчиков и 4 девочки. Надо выбрать 3 человека дежурными так, чтобы среди них было 2 мальчика и 1 девочка. Сколькими способами это можно сделать?

(Число сочетаний из 10 по 2 умножить на число сочетаний из 4 по 1)

Ответы для задач с самостоятельным вычислением

№1 15 рукопожатий

№2 840 способов

№3 720дней

№5 120 способов

№6 180 способов

Домашнее задание №835, №841

8 урок Тема: « Самостоятельная работа»

Цель: Проверка знаний учащихся

1.Проверка домашнего задании

№^ 835 Сколько четных четырехзначных чисел, в которых цифры не повторяются, можно записать с помощью цифр а) 1,2,3,7 . б) 1,2,3,4.

28

Решение

а) Наши числа должны оканчиваться четной цифрой, такая цйфра в условии одна это цифра 2 , поставим ее на последнее место, а оставшиеся 3 цифры будем переставлять, число таких перестановок равно 3! = 6 .Значит можно составить 6 четных чисел

б) рассуждаем как в примере а) поставив на последнее место цифру 2 получим 6 четных чисел, поставив на последнее место цифру 4 получим еще 6 четных чисел,

значит всего 12 четных чисел

№841 Сколькими способами из класса , где учатся 24 учащихся можно выбрать: а) двух дежурных; б) старосту и его помощника ?

Решение

а) т.к. дежурными могут быть любые 2 человека из 24 , то количество пар равно

С₂₄² = 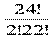= 23 ∙ 24 :2 = 276

б) здесь выдирают упорядоченную пару элементов из 24 элементов , количество таких пар равно А₂₄² = 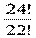= 23 ∙ 24 = 552

Далее предлагается самостоятельная работа

1 вариант решает задания № 1,2,3,4,5.

2 вариант решает задания №6,7,8,9,10.

Решение простейших комбинаторных задач

( по материалам к.р. в апреле 2010 года)

1. Сколькими способами можно расставить на полке пять книг разных авторов?

2.Сколькими способами можно составить полдник из напитка и пирожка, если в меню указаны: чай, кофе, какао и пирожки с яблоком или с вишней?

3.В среду по расписанию в 9 «А» классе должно быть 5 уроков: химия, физика, алгебра, биология и ОБЖ. Сколькими способами можно составить расписание на этот день?

4.Имеются 2 белых лошади и 4 гнедых. Сколькими способами можно

составить пару из лошадей разной масти?

5.Каким числом способов можно разложить 5 различных монет в 5 разных карманов?

29

6.В шкафу на полке лежат 3 шапки различных фасонов и 4 шарфа разных цветов. Сколькими способами можно составить набор из одной шапки и одного шарфа?

7.В финал конкурса красоты вышли 4 участницы. Сколькими способами

можно установить очередность выступления участниц финала красоты?

^ 8.Имеются 4 утки и 3 гуся. Сколькими способами можно из них выбрать две разных птицы?

9.Сколькими способами можно разложить 5 разных писем по 5 разным

конвертам, если в каждый конверт кладется только одно письмо?

10.В коробке хранятся 5 красных и 4 зелёных шара. Сколькими способами можно составить пару из шаров разного цвета?

Ответы для заданий самостоятельной работы

№зад	№1	№2	№3	№4	№5	№6	№7	№8	№9	№10
ответ	120	6	120	8	120	12	24	12	120	20

Примеры задач

В10 по математике:

В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. На вызов выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

Возможное число исходов 10. Число благоприятных исходов 1 (жёлтая машина одна). Искомая вероятность равна 1 к 10 или 0,1.

Ответ: 0,1

Перестановки решение

Задача 1

В пассажирском поезде 17 вагонов. Сколькими способами можно распределить по вагонам 17 проводников, если за каждым вагоном закрепляется один проводник?

Ответ:

17! способами.

Задача 2

На танцплощадке собрались N юношей и N девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце?

Подсказка:

"Зафиксируем" девушек. Тогда разбиение на пары определяется перестановкой юношей.

Ответ:

N! способами.

Задача 3

Сколько существует различных возможностей рассадить 5 юношей и 5 девушек за круглый стол с 10 креслами так, чтобы они чередовались?

Ответ:

2·(5!)² = 28800 возможностей.

Задача 4

В городе Васюки у всех семей были отдельные дома. В один прекрасный день каждая семья переехала в дом, который раньше занимала другая семья. В связи с этим было решено покрасить все дома в красный, синий или зелёный цвет, причём так, чтобы для каждой семьи цвет нового и старого домов не совпадал. Можно ли это сделать?

Решение:

Все семьи города можно разбить на замкнутые цепочки, в которых после каждой семьи будет стоять та, в дом которой семья переехала (может быть, будет всего одна цепочка). В цепочках из чётного числа семей, будем красить дома попеременно в синий и зелёный цвета — тогда каждая семья переедет из синего дома в зелёный или наоборот. А в тех цепочках, где число семей нечётно, покрасим один дом в красный цвет, а оставшееся чётное число домов — попеременно в синий и зелёный. Тогда все дома будут окрашены с выполнением требований задачи.

Ответ:

Можно.

Задача 5

Семнадцать девушек водят хоровод. Сколькими различными способами они могут встать в круг?

Решение:

Первый способ. Зафиксируем одно из мест в круге. Всегда можно повернуть круг так, чтобы на этом месте оказалась первая девушка. Остальные 16 девушек могут расположиться по оставшимся 16 местам 16! способами.
Второй способ. 17 девушек по 17 местам можно расставить 17! способами. Разобьем все эти расстановки на группы, объединив в одну группу расстановки, получающиеся друг из друга поворотами. Очевидно, в каждой группе – по 17 расстановок. Следовательно, групп (то есть способов встать в круг) 17! : 17 = 16!.

Ответ:

16! способами.

Задача 6

а) Сколькими способами 28 учеников могут выстроиться в очередь в столовую?
б) Как изменится это число, если Петю Иванова и Колю Васина нельзя ставить друг за другом?

Решение:

б) Временно уберем из очереди Колю. Оставшихся учеников можно расставить 26! способами, но два из них – перед Петей и после него – запрещены.

Ответ:

а) 28!; б) 26·27!.

Задача 7

Анаграммой называется произвольное слово, полученное из данного слова перестановкой букв. Сколько анаграмм можно составить из слов:
а) "точка"; б) "прямая"; в) "перешеек"; г) "биссектриса"; д) "абракадабра"; е) "комбинаторика"?

Подсказка:

См. задачу 30330.

Ответ:

а) 5! = 120; б) 6! : 2 = 360; в) 8! : 4! = 1680; г) 11! : (2!·3!) = 3326400; д) 11! : (5!·2·2) = 83160; е) 13! : 2⁴ анаграмм.

Задача 8

Даны шесть слов:

ЗАНОЗА

ЗИПУНЫ

КАЗИНО

КЕФАЛЬ

ОТМЕЛЬ

ШЕЛЕСТ

За один шаг можно заменить любую букву в любом из этих слов на любую другую (например, за один шаг можно получить из слова ЗАНОЗА слово ЗКНОЗА. Сколько шагов нужно, чтобы сделать все слова одинаковыми (допускаются бессмысленные)? Приведите пример и докажите, что меньшим числом шагов обойтись нельзя.

Решение:

Ответ: 25. Напишем слова в столбик:

ЗАНОЗА

ЗИПУНЫ

КАЗИНО

КЕФАЛЬ

ОТМЕЛЬ

ШЕЛЕСТ

После всех замен буквы в каждой колонке должны стать одинаковыми. Число замен будет наименьшим, если в каждой колонке сохранить наиболее частую букву (любую из них, если таких букв несколько). Например, в первой колонке можно оставить буквы З или К, они обе требуют четырёх замен. Минимальное число замен равно 4+4+5+4+4+4=25.

Среди слов, которые могут получиться в результате, есть осмысленные, например ЗЕЛЕНЬ, КАПЕЛЬ или КАФЕЛЬ.

Задача 9

a₁, a₂, ..., a₁₀₁ — такая перестановка чисел 2, 3, ..., 102 , что a_k делится на k при каждом k. Найти все такие перестановки.

Решение:

Добавим а₁₀₂ = 1. Мы получили подстановку на множестве {1, 2, ..., 102}. Она распадается на циклы. Но наименьшее число нетривиального (содержащего более одного числа) цикла стоит на месте с номером, большим самого числа. По условию таким числом может быть только 1, следовательно, нетривиальный цикл только один (и состоит из некоторых делителей числа 102, каждый из которых является делителем следующего), а остальные циклы тривиальны. Вот все варианты нетривиальных циклов (их 13):
(1, 102); (1, 2, 102); (1, 3, 102); (1, 6, 102); (1, 17, 102); (1, 34, 102); (1, 51, 102); (1, 2, 6, 102); (1, 2, 34, 102); (1, 3, 6, 102); (1, 3, 51, 102); (1, 17, 34, 102); (1, 17, 51, 102).

Другой подход. Заметим, что произведение целых чисел равно 102, следовательно, каждому упорядоченному разложению 102 на множители соответствует перестановка. Например, разложению 102 = 3· 2·17 соответствует перестановка a₁ = 3, a₃ = 3·2 = 6, a₆ = 102.

Задача 10

В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?

Подсказка:

Сколько шестибуквенных последовательностей не являются словами?

Ответ:

6⁶ – 6! слов.

Задача 11

а) Найдите сумму всех трехзначных чисел, которые можно записать с помощью цифр 1, 2, 3, 4 (цифры могут повторяться).

б) Найдите сумму всех семизначных чисел, которые можно получить всевозможными перестановками цифр 1, ..., 7.

Подсказка:

а) На каждом месте каждая из цифр встречается 4² = 16 раз.

Решение:

б) Найдем сначала сумму цифр разряда единиц. Каждая цифра от 1 до 7 входит (в качестве цифры единиц) в 6! чисел, значит, эта сумма равна 6!·(1 + 2 + ... + 7) = 28·6!. То же верно и для остальных разрядов.

Ответ:

а) 16·(1 + 2 + 3 + 4)·111 = 17760; б) 28·6!·1111111.

.

Лекция № 7

Вероятность. Теоремы сложения и умножения вероятностей

Элементы комбинаторики

Группы, составленные из каких-либо элементов, называются соединениями.

Различают три вида основных соединений: размещения, перестановки и сочетания.

Задачи, в которых производится подсчёт возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.

Размещения

Размещениями из n элементов по m элементам называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.

Число размещений из n по m элементам обозначается символом 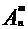и вычисляется по формуле:

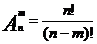(1)

Перестановки

Перестановками из n элементов называются такие соединения, которые отличаются друг от друга лишь порядком следования элементов.

Число перестановок обозначают символом P_n.

Перестановки представляют собой частный случай размещения и вычисляются по формуле:

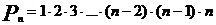(2)

Сочетания

Сочетаниями из n элементов по m называются такие соединения, каждое из которых содержит n элементов, взятых из данных m элементов, и отличается от другого хотя бы одним элементом, обозначается 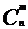и вычисляется о формуле:

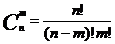(3)

Пример 1.1.Вычислить:

1) ;

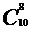2) Р₄.

Решение.

Применяем формулы (2) и (3):

1)

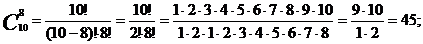
2)