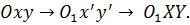def.Параболойназывается геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
Обозначим p – расстояние от фокуса до директрисы; р – параметр параболы.
F – фокус;
l – директриса;
M – произвольная точка параболы;
p – параметр параболы (расстояние от F до l). 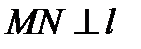
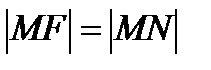 – по определению параболы.
– по определению параболы.
Выберем систему координат следующим образом: ось OXпроведем через фокус F перпендикулярно директрисе l. Начало координат О поместим на равных расстояниях от F и l.
M(x;y) – производная точка параболы; F( 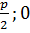 ) – фокус
) – фокус
N(- 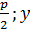 )-основание перпендикуляра,x=
)-основание перпендикуляра,x= 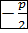 –уравнение директрисы
–уравнение директрисы
|MF|= 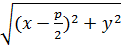 , |MN|=
, |MN|= 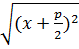 .
.
Из определения следует: 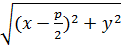 =
= 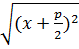 – уравнение параболы в выбранной системе координат.
– уравнение параболы в выбранной системе координат.
Преобразуем это уравнение: 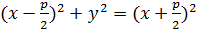
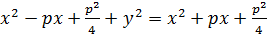
(1) -каноническое уравнение параболы.
II. Исследование формы параболы 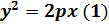
1) Из (1) получим: 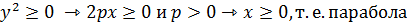 (1) расположена справа от оси OY (в правой полуплоскости)
(1) расположена справа от оси OY (в правой полуплоскости)
2) 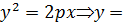 +
+ 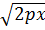 , любому х соответствуют два значения у
, любому х соответствуют два значения у 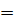 +
+ 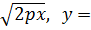 –
– 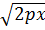 , значит (1) симметрична относительно оси Оx.
, значит (1) симметрична относительно оси Оx.
3) Точка пересечение с Ох (с осью симметрии):у=0Þх=0.
О(0;0)-вершина параболы.
4) Если х®+∞, то |y|®+∞.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAawuswsQA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPTWvCQBC9F/wPywi9NRuFlhCzigSkRdpD1Iu3MTsm wexszK4m7a/vFgre5vE+J1uNphV36l1jWcEsikEQl1Y3XCk47DcvCQjnkTW2lknBNzlYLSdPGaba DlzQfecrEULYpaig9r5LpXRlTQZdZDviwJ1tb9AH2FdS9ziEcNPKeRy/SYMNh4YaO8prKi+7m1Gw zTdfWJzmJvlp8/fP87q7Ho6vSj1Px/UChKfRP8T/7g8d5icz+HsmXCCXvwAAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAGsLrMLEAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
II. Различные виды парабол
1) y2=2px – симметрична относительно Оx,
ветви вправо (в правой полуплоскости),
О(0;0)-вершина.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEASj3jpcYA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2vCQBDF70K/wzIFb7pRqEjqRiQglmIPWi+9TbOT P5idjdmtpv30nYPgbYb35r3frNaDa9WV+tB4NjCbJqCIC28brgycPreTJagQkS22nsnALwVYZ0+j FabW3/hA12OslIRwSNFAHWOXah2KmhyGqe+IRSt97zDK2lfa9niTcNfqeZIstMOGpaHGjvKaivPx xxl4z7cfePieu+Vfm+/25aa7nL5ejBk/D5tXUJGG+DDfr9+s4C+EVp6RCXT2DwAA//8DAFBLAQIt ABQABgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFw ZXhtbC54bWxQSwECLQAUAAYACAAAACEASj3jpcYAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJz L2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIsDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt">
2)
y
2=–2px – симметрична относительноОх,
ветви влево
(в левой полуплоскости),
О(0;0)-вершина.
3) х2=2pу – симметрична относительноОу,
ветви вверх (в верхней полуплоскости),
О(0;0)-вершина.
4) х2=–2pу – симметрична относительноОу,
ветви вниз (в нижней полуплоскости),
О(0;0)-вершина.
§6. Преобразование координат
I. Параллельный перенос
На плоскости введена прямоугольная система координат Oxy. Перенесем точку O в точку  и построим новую систему координат
и построим новую систему координат 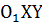 , причем
, причем 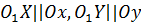 , направления осей совпадают, единицы масштаба одинаковые.
, направления осей совпадают, единицы масштаба одинаковые.
Говорят, что выполнен параллельный перенососей координат,
причем точка 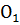 имеет координаты
имеет координаты 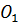 (a,b) в системе Oxy.
(a,b) в системе Oxy.
M – произвольная точка плоскости.
M(x,y) – в старой системе координат Oxy.
M(X,Y) – в новой системе координат 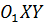 .
.
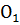 (a,b) – координаты точки
(a,b) – координаты точки 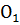 в старой системе координат.
в старой системе координат.
Справедливы формулы:
- формулы, выражающие новые координаты через старые.
- формулы, выражающие старые координаты через новые.
Эти формулы называются формулами параллельного переноса.
Замечание 1.Уравнения вида
(1)
(2)
(2)
определяютпараболу с вершиной в точке 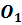 (a,b).
(a,b).
Действительно, с помощью формул параллельного переноса:
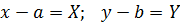 получим: (1) Þ
получим: (1) Þ 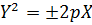 ,
,
(2) Þ 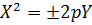 –
–
параболы с вершиной в новом начале координат  .
.
Осью симметрии параболы (1) является прямая 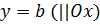 .
.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAlYweAccA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPzWvCQBTE70L/h+UVetNNQ1slZhUJSEXagx8Xb8/s ywdm36bZrab9611B8DjMzG+YdN6bRpypc7VlBa+jCARxbnXNpYL9bjmcgHAeWWNjmRT8kYP57GmQ YqLthTd03vpSBAi7BBVU3reJlC6vyKAb2ZY4eIXtDPogu1LqDi8BbhoZR9GHNFhzWKiwpayi/LT9 NQrW2fIbN8fYTP6b7POrWLQ/+8O7Ui/P/WIKwlPvH+F7e6UVxOM3uJ0JR0DOrgAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAJWMHgHHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
Осью симметрии параболы (2) является прямая
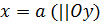
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA/lQnQscA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE70L/w/IKvenGQINNXUUCoUXsweilt9fs Mwlm36bZrYn++m6h4HGYmW+Y5Xo0rbhQ7xrLCuazCARxaXXDlYLjIZ8uQDiPrLG1TAqu5GC9epgs MdV24D1dCl+JAGGXooLa+y6V0pU1GXQz2xEH72R7gz7IvpK6xyHATSvjKEqkwYbDQo0dZTWV5+LH KNhm+Qfuv2KzuLXZ2+606b6Pn89KPT2Om1cQnkZ/D/+337WCOHmBvzPhCMjVLwAAAP//AwBQSwEC LQAUAAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hh cGV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAP5UJ0LHAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRy cy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACMAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
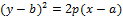 |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA6rcYAsMA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdC/MP4Q6403QKo6VjFCmIg+jCx8bdtbm2 ZZqbThO1+vVmIbg8nPdk1plaXKl1lWUFX8MIBHFudcWFgsN+MUhAOI+ssbZMCu7kYDb96E0w1fbG W7rufCFCCLsUFZTeN6mULi/JoBvahjhwZ9sa9AG2hdQt3kK4qWUcRSNpsOLQUGJDWUn53+5iFKyy xQa3p9gkjzpbrs/z5v9w/Faq/9nNf0B46vxb/HL/agXxOMwPZ8IRkNMnAAAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEA6rcYAsMAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt">
.
Пример 6.1. Найти координаты вершины параболы, построить график:
а) 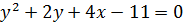 ; б)
; б) 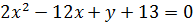 .
.
Замечание 2.Если в уравнениях эллипса и гиперболы заменить х и у соответственно на 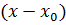 и
и 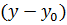 , то полученные уравнения будут определять те же линии, но со смещенным центром (вместо
, то полученные уравнения будут определять те же линии, но со смещенным центром (вместо 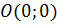 будет
будет 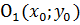 ).
).
II. Поворот осей координат
На плоскости задана прямоугольная система координат Oxy. Повернем координатные оси на угол α, не меняя начала координат. Получим новую систему координат OХУ.
М – произвольная точка плоскости,
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA9gox78QA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPTWvCQBC9F/oflhF6qxsDLZK6igSCIvUQ66W3MTsm wexsml2T1F/fFYTe5vE+Z7EaTSN66lxtWcFsGoEgLqyuuVRw/Mpe5yCcR9bYWCYFv+RgtXx+WmCi 7cA59QdfihDCLkEFlfdtIqUrKjLoprYlDtzZdgZ9gF0pdYdDCDeNjKPoXRqsOTRU2FJaUXE5XI2C XZrtMT/FZn5r0s3ned3+HL/flHqZjOsPEJ5G/y9+uLc6zI9iuD8TLpDLPwAAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAPYKMe/EAAAA3AAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= " filled="f" stroked="f" strokeweight=".5pt">
М(x;y) – в старой системе
координатОху,
M(X;Y) – в новой системе
координат OXY.
Тогда 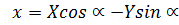 (3) –
(3) –
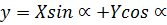
формулы поворота координатных осей.
III. Общий случай преобразования координат
Пусть на плоскости заданы две декартовы прямоугольные системы координат Oxyи O1XY с разным началом и разными направлениями осей.
О1(а,b)-координаты О1 в системе координат Oxy,
α – угол, который образует ось O1Xc осью Ox.
Возьмем т.М. М(x;y) – в координатной плоскости Oxy,
M(X;Y)– в координатной плоскости O1ХУ.
Введем промежуточную систему координат O1 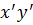 , где O1
, где O1 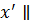 Ox, O1
Ox, O1 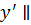 Oy.
Oy.
Переход от Oxy к O1XY осуществляется за два шага:
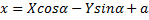 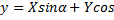 α+b α+b |
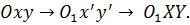
Тогда
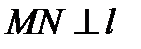
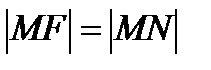 – по определению параболы.
– по определению параболы.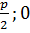 ) – фокус
) – фокус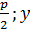 )-основание перпендикуляра,x=
)-основание перпендикуляра,x= 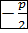 –уравнение директрисы
–уравнение директрисы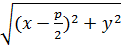 , |MN|=
, |MN|= 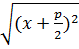 .
.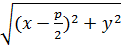 =
= 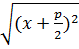 – уравнение параболы в выбранной системе координат.
– уравнение параболы в выбранной системе координат.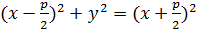
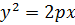
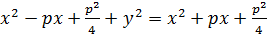
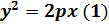
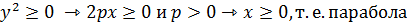 (1) расположена справа от оси OY (в правой полуплоскости)
(1) расположена справа от оси OY (в правой полуплоскости)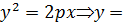 +
+ 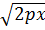 , любому х соответствуют два значения у
, любому х соответствуют два значения у 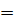 +
+ 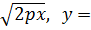 –
– 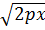 , значит (1) симметрична относительно оси Оx.
, значит (1) симметрична относительно оси Оx.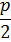
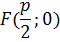
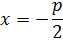
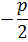
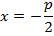
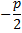
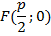
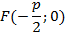
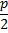
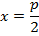
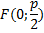
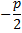
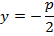
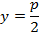
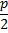
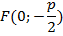
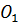 и построим новую систему координат
и построим новую систему координат 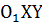 , причем
, причем 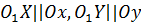 , направления осей совпадают, единицы масштаба одинаковые.
, направления осей совпадают, единицы масштаба одинаковые.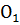 имеет координаты
имеет координаты 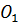 (a,b) в системе Oxy.
(a,b) в системе Oxy.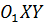 .
.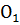 (a,b) – координаты точки
(a,b) – координаты точки 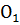 в старой системе координат.
в старой системе координат.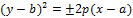
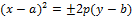
 (a,b).
(a,b).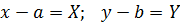 получим: (1) Þ
получим: (1) Þ 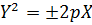 ,
,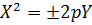 –
– .
.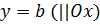 .
.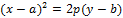
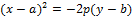
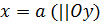
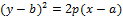
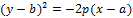
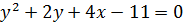 ; б)
; б) 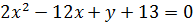 .
.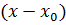 и
и 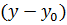 , то полученные уравнения будут определять те же линии, но со смещенным центром (вместо
, то полученные уравнения будут определять те же линии, но со смещенным центром (вместо 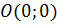 будет
будет 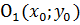 ).
).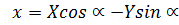 (3) –
(3) –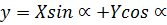
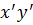 , где O1
, где O1 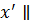 Ox, O1
Ox, O1 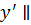 Oy.
Oy.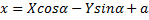
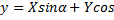 α+b
α+b