I. Определение. Каноническое уравнение.
def.
| М |
 |
 |
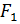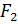| 2с |
Обозначим:М – произвольная точка гиперболы;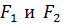 
– фокусы;
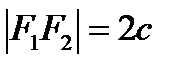– расстояние между фокусами;
2а – постоянная величина, равнаяразности расстояний от М до фокусов.
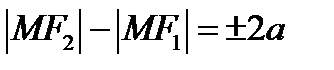(1) – по определению гиперболы
(«+», если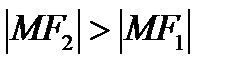 
; «–» , если 
).
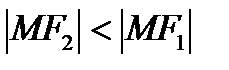2с>2а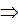 
с>а (одна сторона больше разности двух других сторон).
| у |
 |
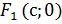| М(x;y) |
 |
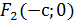| х |
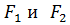, начало координат поместим в середину отрезка 
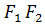. Ось OY через серединуотрезка 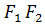перпендикуляноOX.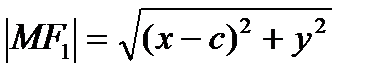
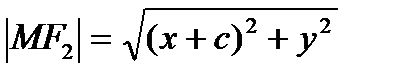
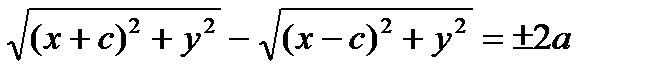(2) – уравнение гиперболы в выбранной
системе координат.
Преобразовав это уравнение аналогично выводу в §3, получим:
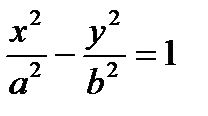(3) – каноническое уравнение гиперболы, где 
.
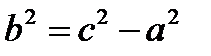II. График гиперболы
1. Симметрия
Гипербола имеет две оси симметрии – осьOx и ось Oy, и центр симметрии – начало координат O(0;0).
2. Вершины. Действительные и мнимые оси
Вершины гиперболы – это точки пересечения гиперболыс осями симметрии, т.е. с осьюOx и осьюOy.
С осью Ох: у=0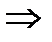 
, 
.
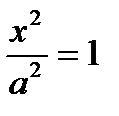
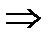
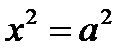
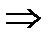
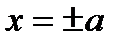
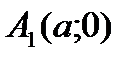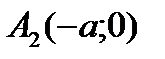С осью Оу: х=0 
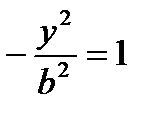
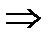нет действительных корней, гипербола не пересекается с Оу.
Итак, две вершины: 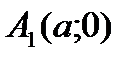и .
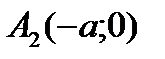def.Отрезок А1А2 и его длина 2а называется действительной осьюгиперболы.
Возьмем на оси Оу две точк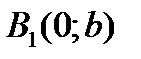и 
и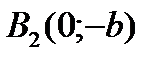 
.
def.Отрезок В1В2 и его длина 2b называется мнимой осьюгиперболы.
а – действительная полуось,b – мнимая полуось гиперболы.
3.
 |
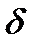| М |
| l |
def. Прямая называется асимптотой кривой, если расстояние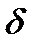 
от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность.
Гипербола 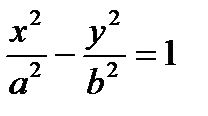имеет две асимптоты:
, 
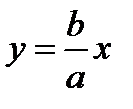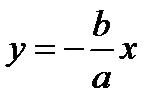– уравнение асимптот гиперболы.
4. График гиперболы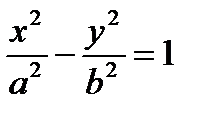 
.
1) Построить (характеристический) прямоугольник со сторонами, параллельными осям Ох и Оу и проходящими на оси Ох на расстоянии а от точки О(0;0) по обе стороны, на оси Оу – на расстоянии b.
2) Провести асимптоты гиперболы по диагоналям прямоугольника.
3)
| F2 |
| –c |
| F1 |
| c |
| х |
| a |
| у |
| 0 |
| b |
| B1 |
| –b |
| B2 |
| A2 |
| A1 |
| –a |
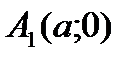и 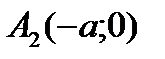и построить график гиперболы.А1, А2– вершины гиперболы,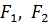 
– фокусы гиперболы.