Рангово-бисериальный коэффициент корреляции

В тех случаях, когда одна переменная измеряется в дихотомической шкале (переменная X), а другая в ранговой шкале (переменная Y), используется рангово-бисериальный коэффициент корреляции. Мы помним, что переменная X, измеренная в дихотомической шкале, принимает только два значения (кода) 0 и 1. Особо подчеркнем: несмотря на то, что этот коэффициент изменяется в диапазоне от -1 до +1, его знак для интерпретации результатов не имеет значения. Это еще одно исключение из общего правила.

Расчет этого коэффициента производится по формуле:

где

X1 — средний ранг по тем элементам переменной Y, которым соответствует код (признак) 1 в переменной X;

X0 — средний ранг по тем элементам переменной Y, которым соответствует код (признак) 0 в переменной X;

N— общее количество элементов в переменной X.

Решим следующий пример с использованием рангово-бисериального коэффициента корреляции.

Задача 11.8. Психолог проверяет гипотезу о том, существуют ли тендерные различия в вербальных способностях.

Решение.Для решения данной задачи 15 подростков разного пола были проранжированы учителем литературы по степени выраженности вербальных способностей. Полученные данные представим сразу в виде таблицы 11.11:

Таблица 11.11

№ испытуемого п/п	Пол	Ранги вербальных способностей

В данном случае правильность ранжирования можно не проверять, поскольку нет совпадающих рангов и ранжирование проводится по порядку.

В таблице 11.11 юноши обозначены кодом 1, а девушки 0. В нашем случае юношей 9 человек, а девушек 6.

Прежде чем произвести расчет по формуле (11.17), найдем необходимые величины т.е. средние значения рангов отдельно для юношей и для девушек.

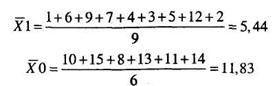
Вычисляем R_эмп по формуле (11.17):

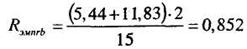
Проверим значимость полученного коэффициента корреляции с помощью формулы (11.9); при k = п - 2 = 15 — 2 = 13:

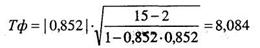
Число степеней свободы в нашем случае будет равно k = 13. По таблице 16 Приложения 1 для k = 13 находим критические значения критерия Стьюдента, они равны соответственно для Р ≤, 0,05 t_Kp = 2,16 и для Р ≤, 0,01 t_Kp = 3,01. В принятой форме записи это выглядит так:

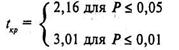
Строим «ось значимости»:

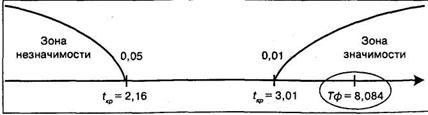
Результат попал в зону значимости. Поэтому принимается гипотеза H₁ согласно которой полученный рангово-бисериальный коэффициент корреляции значимо отличается от нуля. Иными словами, на данной выборке подростков обнаружены значимые тендерные различия по степени выраженности вербальных способностей.

Для применения рангово-бисериального коэффициента корреляции необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в разных шкалах: одна X — в дихотомической шкале; другая Y— в ранговой шкале.

2.Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

3.Для оценки уровня достоверности рангово-бисериального коэффициента корреляции следует пользоваться формулой (11.9) и таблицей критических значений для t-критерия Стьюдента при k = п - 2.

11.9. Корреляционное отношение Пирсона η

Все рассмотренные выше коэффициенты корреляции служат для выявления только линейной зависимости между признаками. Для измерения нелинейной зависимости К. Пирсон предложил показатель, который он назвал корреляционным отношением. Напомним, что коэффициент корреляции r_xy (формула 11.1), который был введен Пирсоном, характеризует связь между переменными X и Υ с точки зрения прямой или обратной пропорциональности, иными словами, получаемая связь между переменными является согласованной и такой, что с увеличением одной переменной другая (в среднем) либо только увеличивается, либо только уменьшается (в среднем). При этом в первом случае получается положительный коэффициент корреляции, во втором отрицательный.

Корреляционное отношение описывает искомую связь, условно говоря, с двух сторон: со стороны переменной X по отношению к Υ, и со стороны переменной Υ по отношению к X. Соответственно этому корреляционное отношение представляет собой два показателя, обозначаемые как h_yx и h_xy . Они вычисляются отдельно друг от друга. Однако они связаны между собой, поскольку при строго линейной зависимости между переменными Х и Y имеет место равенство h_yx = h_xy В этом случае величины обоих показателей корреляционного отношения совпадают с величиной коэффициента корреляции Пирсона.

Показатели корреляционного отношения вычисляются по следующим двум формулам:

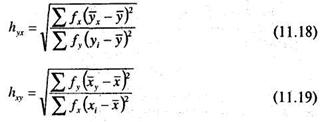
здесь х и у общие, а х_у и у_х — групповые средние арифметические, f_y и f_x частоты рядов Х и Y. Согласно этим формулам оба показателя всегда положительны и располагаются в интервале от 0 до +1.

Подчеркнем, что, как правило, h_yx ≠ h_xy. Равенство между этими коэффициентами возможно лишь при наличии строго линейной связи между коррелируемыми переменными. Именно поэтому различие между h_yx и h_xy будет означать наличие не линейной, а связи более сложного типа между коррелируемыми признаками.

Для вычисления корреляционного соотношения h_yx (Y по X) или h_xy (Х по Y) необходимо выполнить следующие действия:

1) расположить по порядку исходные данные по X от меньшей величины к большей, при этом сохранив значения соответствующих величин Y по отношению к X;

2) определить частоты переменной X — обозначение f_x;

3) подсчитать арифметические (частные) средние по переменной Y для соответствующей частоты f_x — обозначение у_х;

4) найти варианты (неповторяющиеся значения) величины X — обозначение х_i,

5) расположить по порядку исходные данные по Y от меньшей величины к большей, при этом сохранив значения соответствующих величин Х по отношению к Y;

6) определить частоты переменной Y — обозначение f_y;

7) подсчитать арифметические (частные) средние по переменной Xдля соответствующей частоты f_y — обозначение х_y;

8) найти варианты (неповторяющиеся значения) переменной Y — обозначение у_i:,

9) определить общие средние по переменной X и Y обозначение х и у;

10)произвести расчет по формулам (11.18) и (11.19);

11)определить уровень значимости полученных показателей корреляционного отношения по таблице критических значений для t -критерия Стьюдента при k = п — 2.

На конкретном примере рассмотрим, как производить расчет показателей корреляционного отношения.

Задача 11.9.Психолог у 8 подростков сравнивает баллы по третьему, математическому, субтесту теста Векслера (переменная X) и оценки по алгебре (переменная Y). Интересующие психолога вопросы можно сформулировать двояко. Первый вопрос — связана ли успешность решения третьего субтеста Векслера с оценками по алгебре? И второй — связаны ли оценки по алгебре с успешностью решения третьего субтеста Векслера?

Решение. Представим экспериментальные данные в следующем виде:

Значения X 8 18 18 10 16 10 8 14

Значения Y 2 3 4 5 4 4 3 5

Если мы подсчитаем коэффициент линейной корреляции Пирсона по формуле (11.1) то получим величину r_xy = 0,244. Этот коэффициент незначим и, следовательно, линейной связи между переменными Х иY нет. Нужно выяснить — существует ли между двумя вышеприведенными переменными другой тип связи?

Произведем расчет согласно пунктам 1 — 11.

1. Расставим по порядку величины X от меньшей к наибольшей, сохраняя их соответствие с исходными данными по Y:

Значения X 8 8 10 10 14 16 18 18

Значения Y 2 3 4 5 5 4 3 4

2. Определяем частоты переменной X(обозначаемые как/) и соответствующие им неповторяющиеся значения переменной X (обозначающиеся как х). Частоты вычисляются по правилу, изложенному в главе 3, раздел 3.2. Согласно этому правилу, если какая-либо переменная величина встречается в анализируемом ряду один, два, три и большее число раз, то этой величине проставляется частота, равная соответственно одному, двум, трем и большим значениям. Так, в нашем случае число 8 встречается два раза — следовательно, его частота равна 2, число 10, также два раза, следовательно, его частота также равна 2.

Частоты переменной X , f_x 2 2 1 1 2

Неповторяющиеся значения переменной X х. 8 10 14 16 18

Проверим правильность подсчета частот — их сумма должна равняться числу варьирующих величин переменной X.

Σf_x=2+2+1 + 1+2 = 8

3. Подсчитываем арифметические частные средние для переменной Y по отношению к переменной X. Для этого одинаковым значениям X ставим в соответствие их среднее арифметическое по Y следующим образом: в исходных данных двум значениям 8 и 8 по X соответствовали величины 2 и 3 по Y— следовательно, одному значению X (равному 8) — будет соответствовать частное среднее по Y равное (2 + 3)/ 2 = 2,5. Значению 10 по X — (4 + 5)/2 = 4,5 . Соответствие между числами 14 и 5 и 16 и. 4 остается неизменным. Значению 18 по вставим (3 + 4)/2 = 3,5.

Таким образом построено новое распределение, где f_x — частота для переменной X. Расположим полученные величины в следующем виде:

Частоты по X f_x 2 2 1 1 2

Значения X без повторов х_i. 8 10 14 16 18

Частные средние по Y y_x 2,5 4,5 5 4 3,5

4. Расположим по возрастающей экспериментальные данные по Y

Значения Y 2 3 3 4 4 4 5 5

Значения X 8 8 18 10 16 18 10 14

5.Подсчитаем соответствующие частоты:

Частоты переменной Y f_у 1 2 3 2

Неповторяющиеся значения Y у_i. 2 3 4 5

Проверка правильности подсчета частот:Σ f_у =1 + 2 + 3 + 2 = 8

6. Подсчитаем соответствующие частные средние по X:

(8 + 8)/2=8, (8 + 18)/2=13, (10 + 16 + 18)/3=14,7 и (10+14)/2=12

Расположим полученные величины в следующем виде:

Частоты по Υ f_y 1 2 3 2

Значения Y без повторов y_i 2 3 4 5

Частные средние по X x_y 8 13 14,7 12

7. Теперь подсчитаем общие средние.

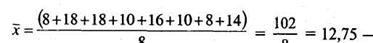
– общее среднее по X.

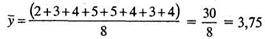
— общее среднее по Y.

8. Все готово для расчета по формулам (11.18) и (11.19)

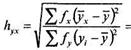
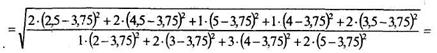
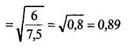
Подсчитаем теперь

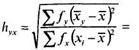
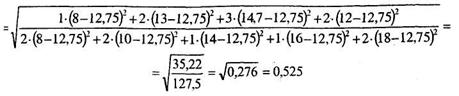
В результате получено два неравных показателя корреляционного отношения. Для проверки их значимости следует применить формулу (11.9) для k = п - 2.

Проверим на уровень значимости первый показатель.

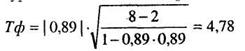
По таблице 16 Приложения 1 для £ = и-2 = 8-2 = 6 находим:

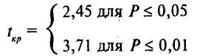
Строим соответствующую «ось значимости»:

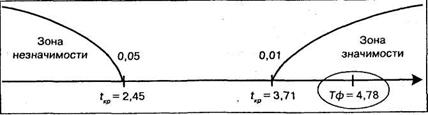
Можно сделать вывод о том, что полученный показатель значим. Принимается гипотеза H₁.

Подсчитываем уровень значимости второго показателя:

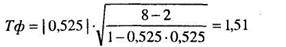
Поскольку критические значения уже найдены выше, строим соответствующую «ось значимости»:

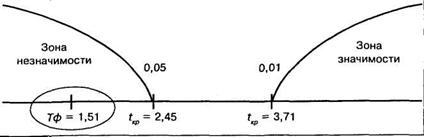
Следовательно, полученный показатель незначим. Принимается гипотеза H_о.

Таким образом, можно сделать вывод о том, что в данном случае есть значимое влияние Y на X, а обратное влияние Х на Y незначимо. Следовательно, решение искомой задачи может звучать так: хорошее знание алгебры влияет на эффективность работы с третьим субтестом Векслера, и, напротив, успешное решение третьего субтеста Векслера никак не сказывается на овладении учащимися алгеброй.

Разумеется, корреляционное отношение Пирсона не дает возможности" установить характер выявленной зависимости — она может быть параболической, кубической, логарифмической и др. Из результатов анализа ясно только одно: связь между переменными Х и Y носит нелинейный характер. Более точно характер связи можно определить с помощью метода регрессионного анализа.

К сожалению, в психологии метод корреляционного отношения не нашел широкого распространения. Многие исследования, использующие корреляционный анализ, ограничивались нахождением только линейной зависимости между переменными, хотя нельзя исключить вероятность того, что реальные связи были нелинейными. Напомним, что в нашем примере коэффициент корреляции Пирсона, подсчитанный по формуле (11.1) r = 0,243 оказался незначимым. Однако, как это было установлено с помощью метода корреляционного отношения, связь, с одной стороны, действительно была незначимой, а с другой, напротив, высокозначимой.

Для применения корреляционного отношения Пирсона необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.

2. Предполагается, что обе переменные имеют нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

4. Для оценки уровня достоверности корреляционного отношения

Пирсона следует пользоваться формулой (11.9) и таблицей критических значений для t-критерия Стьюдента при k = п — 2.

Множественная корреляция

Наряду с анализом связей между двумя рядами данных можно проводить анализ многомерных корреляционных связей. Наиболее простым случаем нахождения подобной зависимости является вычисление коэффициентов множественной корреляции между тремя переменными X, Y и Z. В соответствии с числом переменных вычисляются три коэффициента множественной корреляции. Собственно говоря, коэффициент множественной корреляции оценивает тесноту линейной связи одной переменной, например X, с двумя остальными, Y и Z, и обозначается как г. При оценке тесноты линейной связи переменной Y с переменными X и Z, коэффициент множественной корреляции обозначается как r_x(yz).

Вычисление коэффициентов множественной корреляции базируется на коэффициентах линейной корреляции между переменными X и Y — r_ху, X и Z — r_xz, Y и Z — r_yz. Для вычисления одного из коэффициентов множественной корреляции, например r_х(уz), используется следующая формула:

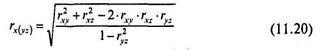
где r_ху,, r_xz, r_уг — коэффициенты линейной корреляции между парами переменных X и Y, X и Z, Y и Z.

Коэффициент множественной корреляции принимает значения от 0 до 1. Значимость этого коэффициента оценивают по величине t-критерия Стьюдента с числом степеней свободы k = п - 3.

Собственно говоря, формулы для вычисления коэффициентов r_y(xz): и r_z(xy) аналогичны формуле (11.20) и получаются из нее перестановкой индексов.

Формула для вычисления коэффициента r_y(xz):

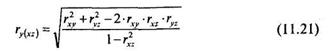
Формула для вычисления коэффициента r_z(xy):

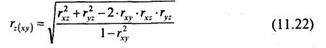
Задача 11.9.10 менеджеров оценивались по методике экспертных оценок психологических характеристик личности руководителя (см. Психологические тесты. Т. 2. Под. ред. А.А. Карелина. М. Владос. 1999. Стр. 99). 15 экспертов производили оценку каждой психологической характеристики по пятибальной системе. Психолога интересуют три вопроса: в какой степени тактичность (переменная X)одновременно связана с требовательностью (переменная Y)и критичностью (переменная Z); в какой степени требовательность одновременно связана с тактичностью и критичностью; и, наконец, в какой степени критичность одновременно связана с тактичностью и требовательностью?

Решение. Результаты исследования сразу представим в виде таблицы 11.12, в которой произведем некоторые нужные вычисления.

Таблица 11.12

Испы­туе­мые п/п	Так­тич­ность X	Требо­ватель­ность Y	Кри­тич­ность Z	Х- X	Y-Y	ZZ	Х-Y	Y-Z	X Z
Сумма

Для подсчета необходимых коэффициентов множественной корреляции используем следующие выражения:

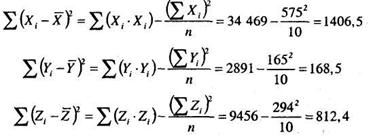
Отсюда:

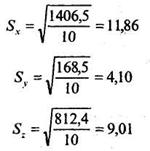
Далее:

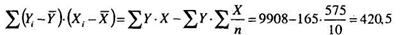
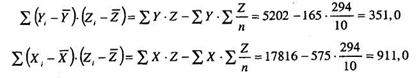
Тогда коэффициенты Пирсона таковы:

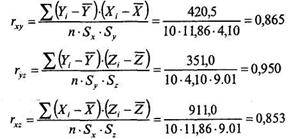
Для вычисления r_x(yz) подставляем полученные величины в формулу (11.20), получаем:

Для вычисления r_y(xz) подставляем полученные величины в формулу (11.21), получаем:

Для вычисления r_z(xy) подставляем полученные величины в формулу (11.22), получаем:

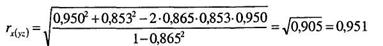
Поскольку из трех коэффицентов, первый r_x(yz) оказалея наименьшим по абсолютной величине, то проверим значимость только этого коэффициента по хорошо знакомой нам формуле (11.9) при k = п - 3:

По таблице 16 Приложения 1 для t-критерия Стьюдента при k= 10-3 = 7 находим, что

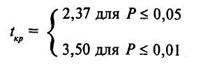
Строим соответствующую «ось значимости»:

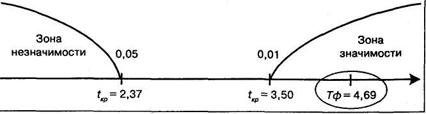
Полученный коэффициент множественной корреляции попал в зону значимости. Следовательно, необходимо принять гипотезу Я, об отличии полученного коэффициента от нуля. Очевидно также, что остальные коэффициенты множественной корреляции также окажутся в зоне значимости. Поэтому возможна следующая интерпретация полученного результата — все три оцениваемых качества оказывают существенное влияние друг на друга, иными словами, такие качества личности менеджера, как критичность, тактичность и требовательность, выступают единым комплексом и в очень большой степени необходимы для успешности его профессиональной работы.

Для применения множественного коэффициента корреляции необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.

2. Предполагается, что все переменные имеют нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.

4. Для оценки уровня достоверности корреляционного отношения Пирсона следует пользоваться формулой (11.9) и таблицей критических значений для t-критерия Стьюдента при k = п - 3.

Частная корреляция

Название «частная корреляция» был впервые использовано в работе Д. Юла в 1907. Смысл этого понятия иллюстрирует следующий пример. Предположим, что при обработке некоторых данных удалось обнаружить значимую отрицательную корреляцию между длиной волос и ростом (т.е. люди низкого роста обладают более длинными волосами). На первый взгляд это может показаться странным: однако, если включить в расчет еще один признак — переменную «пол» и использовать не линейную, а частную корреляцию, то результат получит закономерное объяснение, поскольку женщины в среднем имеют более длинные волосы, чем мужчины, а их рост в среднем ниже, чем у мужчин. После учета переменной «пол» частная корреляция между длиной волос и ростом может оказаться близкой к единице. Иными словами, если одна величина коррелирует с другой, то это может быть отражением того факта, что они обе коррелируют с третьей величиной или с совокупностью величин.

Если известна линейная связь между парами переменных X, Y и Z, то можно подсчитать частные коэффициенты корреляции, показывающие линейную корреляционную зависимость между двумя переменными при постоянной величине третьей переменной. Для определения частного коэффициента корреляции между переменными Х и Y при постоянной величине переменной Z используют формулу:

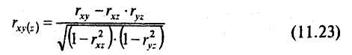
Заключение (z) в скобки означает, что влияние переменной Z на корреляцию между X и Y постоянно. В том случае, если бы влияния переменной Z не было бы совсем, мы бы получили обычный коэффициент корреляции Пирсона между переменными X и Y (который уже подсчитан выше и равен 0,865).

Аналогично строят частные корреляционные зависимости между X и Z (при постоянной Y) и Y и Z (при постоянной X).

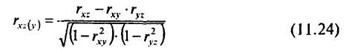
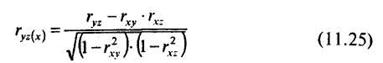
Значимость частного коэффициента корреляции оценивают по величине Тф, подсчитанной по формуле (11.9) для t-критерия Стьюдента с числом степеней свободы k = п - 2.

Задача 11.10.В условиях предыдущей задачи психолога опять интересуют три вопроса: в какой степени тактичность (X) связана с требовательностью (Y), при условии того, что критичность (Z) при этом остается неизменной; в какой степени тактичность (X) связана с критичностью (Z) при условии того, что требовательность (Y) остается неизменной; в какой степени требовательность (Y) связана с критичностью (Z), при условии того, что тактичность (X) остается неизменной?

Решение. На эти вопросы может ответить вычисление коэффициентов частной корреляции по формулам (11.23), (11.24), (11.25).

Для ответа на первый вопрос задачи рассчитаем частный коэффициент корреляции по формуле (11.23):

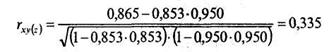
Для ответа на второй вопрос задачи рассчитаем частный коэффициент корреляции по формуле (11.24):

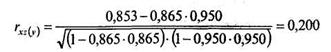
Для ответа на третий вопрос задачи рассчитаем частный коэффициент корреляции по формуле (11.25):

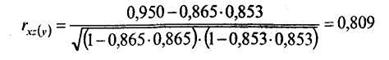
Проверим на значимость первый коэффициент частной корреляции.

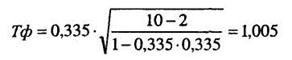
По таблице 16 Приложения 1 для t-критерия Стьюдента при k- п-2 =10-2 = 8 находим, что

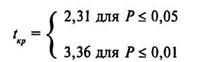
Строим соответствующую «ось значимости»:

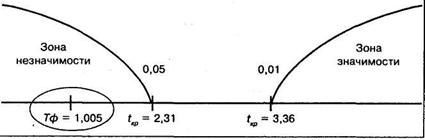
Соответствующий коэффициент частной корреляции попал в зону незначимости, следовательно мы должны принять гипотезу Н_о об отсутствии отличий этого коэффициента от нуля. Подсчет этого коэффициента должен был дать ответ на вопрос — в какой степени тактичность (X) связана с требовательностью (Y), при условии того, что критичность (Z) при этом остается неизменной. Выяснилось, что в подобных условиях связь между тактичностью и требовательностью отсутствует. Напомним, однако, что все линейные коэффициенты корреляции между измеряемыми переменными были высокозначимыми.

Поскольку коэффициент частной корреляции между тактичностью (X) и критичностью (Z) r_xz(y) оказался равным 0,200, что существенно меньше предыдущего частного коэффициента корреляции, то его уровень значимости мы оценивать не будем, а сразу дадим интерпретацию полученного результата. Выяснилось таким образом, что при постоянной требовательности, связь между тактичностью и критичностью отсутствует.

Проверим на уровень значимости последний коэффициент частной корреляции r_yz(x)= 0.809:

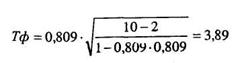
По таблице 16 Приложения 1 для t-критерия Стьюдента при k = п-2 =10-2 = 8 находим, что

Строим соответствующую «ось значимости»:

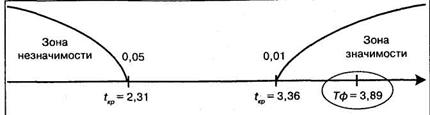
Коэффициент частной корреляции попал в зону значимости, следовательно необходимо принять гипотезу H₁ об отличии этого коэффициента от нуля. Интерпретация полученного результата такова: при условии неизменного уровня тактичности, налицо сильная связь между требовательностью и критичностью.

Для применения частного коэффициента корреляции необходимо соблюдать следующие условия:

1.Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.

2.Предполагается, что все переменные имеют нормальный закон распределения.

3.Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.

4.Для оценки уровня достоверности корреляционного отношения Пирсона следует пользоваться формулой (11.9) и таблицей критических значений для t -критерия Стьюдента при k = n - 2.

В заключение подчеркнем, что содержательное ограничение корреляционного анализа состоит в том, что он позволяет обнаружить только наличие связи и не дает оснований для установления причинно-следственных отношений. Например, можно обнаружить положительную корреляцию между уровнем умственного развития детей старшего дошкольного возраста и календарными сроками смены молочных зубов коренными. Другими словами, чем раньше происходит замена молочных зубов, тем выше показатели умственного развития детей. Следует ли делать вывод о том, что смена зубов способствует умственному развитию детей, или, напротив, ускоренное умственное развитие приводит к более быстрому изменению состава зубов. Оба предположения выглядят одинаково нелепо.

Причина в том, что оба показателя непосредственно отражают индивидуальный темп биологического созревания. Другими словами, они связаны с третьей — латентной переменной, которая недоступна для прямого измерения, но благодаря этой связи оба показателя значимо коррелируют между собой. Формальная логика корреляционного анализа не позволяет исследовать, эти аспекты взаимообусловленности статистических рядов данных.

Глава 12 РЕГРЕССИОННЫЙ АНАЛИЗ

Линейная регрессия

Взаимосвязь между переменными величинами может быть описана разными способами. Например, как было показано в предыдущем разделе, эту связь можно описать с помощью различных коэффициентов корреляции (линейных, частных, корреляционного отношения и т.п.). В то же время эту связь можно выразить по-другому: как зависимость между аргументом (величиной) X и функцией Y. В этом случае задача будет состоять в нахождении зависимости вида Y = F(X) или, напротив, в нахож­дении зависимости вида Х= F(Y). При этом изменение функции в зависимости от изменений одного или нескольких аргументов называется регрессией.

Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X). Эти независимые переменные, а их может быть много, носят название предикторов.

Регрессию выражают с помощью двух уравнений регрессии, которые в самом простом случае выглядят, как уравнения прямой, а именно так:

Y= a0 + al • X (12.1)

Х= b0 + b1 • Y (12.2)

В уравнении 12.1 Y — зависимая переменная, а X— независимая переменная, a0 свободный член, а а1— коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.

В уравнении 12.2 X — зависимая переменная, a Y— независимая переменная, b0 свободный член, а b1 — коэффициент регрессии, или угловой коэффициент, определяющий наклон линии регрессии по отношению к осям координат.

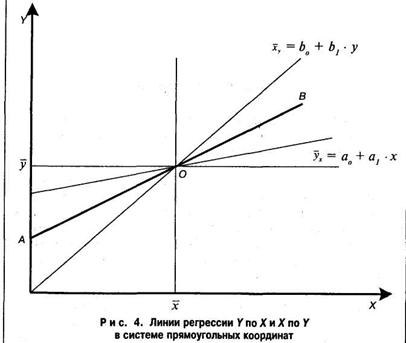
Линии регрессии пересекаются в точке О (х, у), с координатами, соответствующими средним арифметическим значениям корреляционно связанных между собой переменных Х и Y. Линия АВ, проходящая через точку О, соответствует линейной функциональной зависимости между переменными величинами X и Y, когда коэффициент корреляции между X и Y равен r_хy.= 1. При этом наблюдается такая закономерность: чем сильнее связь между X и Y, тем ближе обе линии регрессии к прямой АВ, и, наоборот, чем слабее связь между этими величинами, тем больше линии регресии отклоняются от прямой АВ. При отсутствии связи между X и Y линии регрессии оказываются под прямым углом по отношению друг к другу и в этом случае r_xy = 0.

Количественное представление связи (зависимости) между X и Y (между Y и X)называется регрессионным анализом. Главная задача регрессионного анализа заключается, собственно говоря, в нахождении коэффициентов а0, b0, а1и b1и определении уровня значимости полученных аналитических выражений (12.1) и (12.2), связывающих между собой переменные Х и Y.

При этом коэффициенты регрессии а1и b1показывают, насколько в среднем величина одной переменной изменяется при изменении на единицу меры другой. Коэффициент регрессии а1в уравнении (12.1) можно подсчитать по формуле:

а коэффициент b1 в уравнении (12.2) по формуле (12.4)

где r_xy — коэффициент корреляции между переменными X и Y;

S_x — среднеквадратическое отклонение, подсчитанное для переменной X;

S_y — среднеквадратическое отклонение, подсчитанное для переменной Y.

Коэффициенты регрессии можно вычислить также без подсчета среднеквадратических отклонений по следующим формулам:

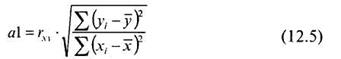
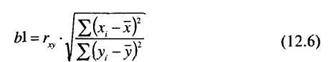
В том случае, если неизвестен коэффициент корреляции, коэффициенты регрессии можно вычислить по следующим формулам:

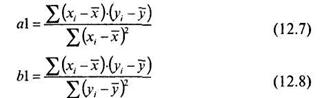
Сравнивая формулы (11.1) (вычисление r_xy), (12.7) и (12.8), видим, что в числителе этих формул стоит одна и та же величина: Σ(x_i –х) (у_i -у). Последнее говорит о том, что величины а1,b1и r_xy взаимосвязаны. Более того, зная две из них — всегда можно получить третью. Например, зная величины а1и b1можно легко получить r_xy:

Формула (12.9) достаточно очевидна, поскольку, умножив а1, вычисленный по формуле (12.3) на b1, вычисленный по формуле (12.24), получим:

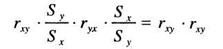
Формула (12.9) очень важна, поскольку она позволяет по известным значениям коэффициентов регрессии а1и b1определить коэффициент корреляции, и, кроме того, сравнивая вычисления по формулам (11.1) и (12.9), можно проверить правильность расчета коэффициента корреляции. Как и коэффициент корреляции, коэффициенты регрессии характеризуют только линейную связь и при положительной связи имеют знак плюс, при отрицательной — знак минус.

В свою очередь свободные члены а0и b1вуравнениях регрессии придется вычислять по следующим формулам. Для подсчета свободного члена a0 уравнения регрессии (12.1) используется формула:

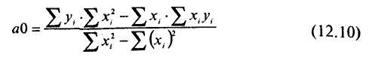
Для подсчета свободного члена b0уравнения регрессии (12.2) используется формула:

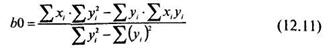
Вычисления по формулам (12.7), (12.8), (12.10) и (12.11) достаточно сложны, поэтому при расчетах коэффициентов регрессии используют, как правило, более простой метод. Он заключается в решении двух систем уравнений. При решении одной системы находятся величины a0 и al, и при решении другой — b0и b1.

Общий вид системы уравнений для нахождения величин a0 и al таков:

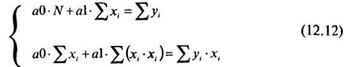
Общий вид системы уравнений для нахождения величин — b0и b1таков:

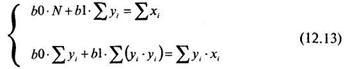
В системах уравнений (12.12) и (12.13) используются следующие обозначения:

N — число элементов в переменной X или в переменной Y,

Σх_ι— сумма всех элементов переменной X,΄

Σy_ι— сумма всех элементов переменной Y,

Σ(y_ι – у) — произведение всех элементов переменной Y друг на друга,

Σ(x_ι – x)— произведение всех элементов переменной Х другна друга,

Σ(x_ι – y_i) — попарное произведение всех элементов переменной X на соответствующие элементы переменной Y.

Приведем несколько примеров линейной регрессии.

Пример 1. Висследовании Ф. Гальтона (который и ввел в науку понятие регрессии) был измерен рост 205 родителей и 930 их взрослых детей (см. таблицу 3.3). При этом, если за Y взять рост ребенка, а за X рост родителя, уравнение регрессии, связывающее рост ребенка с ростом родителей, имеет вид:

Ŷ=Y_i +2/3 (X_i – X) (12.14)

где X и Ŷ средние по всей выборке испытуемых.

Таким образом, зная величины средних по всей выборке и рост одного из родителей — Х_i, из уравнения 12.14 можно подсчитать величину Ŷ, т.е. рост ребенка.

Пример 2.Психологи выявили взаимосвязь между успешностью обучения математике Y и показателем невербального интеллекта X. Было получено следующее уравнение регрессии:

Y = 1+0,025•X (12.15)

Предположим, что показатель невербального интеллекта учащегося равен 132, тогда согласно уравнению регрессии (12.15) можно предсказать его показатель средней успеваемости по математике:

Y =1 +0,025 132 = 4,3

У другого учащегося показатель невербального интеллекта оказался равен 82, тогда его средняя успеваемость по математике составит:

Y= 1 + 0,025•82 = 3,05

Для закрепления основных по