Быстрые» методы — критерии дисперсионного анализа

Как мы только что убедились, дисперсионный анализ достаточно трудоемок. Иногда можно воспользоваться так называемыми «быстрыми» методами — критериями дисперсионного анализа. Общим для этих методов является следующие особенности. Объектом анализа служит здесь изменчивость признака, обусловленная влиянием одного или нескольких факторов. Однако как таковые дисперсии при расчетах с помощью этих методов не вычисляются, а вариативность оценивается другими способами: с помощью величины размаха между максимальными и минимальными значениями признака (критерий Линка и Уоллеса) или посредством оценки диапазона разности рангов (критерий Немени). Использование этих статистических характеристик ускоряет и упрощает процедуру расчетов. Следует иметь в виду, однако, что эти критерии дают приблизительную оценку влияния фактора, и если они не подтверждают влияния, то дисперсионный анализ, возможно, их обнаружит.

10.2.1. Критерий Линка и Уоллеса

Задача 10.4. Психолог провел в обычной школе (1 группа), в школе интернате (2 группа) и в специализированном колледже (3 группа) тестирование мышления с помощью серии задач. Всего было предъявлено 10 задач. В каждой группе было по 8 испытуемых. Фиксировалось количество решенных задач. Психолог выясняет вопрос, влияет ли специфика школьного обучения на эффективность решения задач.

В категории ANOVA задача переформулируется так: регулируемый фактор (независимая переменная) — тип школы (или специфика обучения), результирующий признак — количество решенных задач. Проверяется гипотеза об отсутствии различий в средних и дисперсиях между группами учащихся и, соответственно, об отсутствии влияния регулируемого фактора, т.е. специфики обучения, на продуктивность мыслительной деятельности ученика.

Решение. Результаты тестирования представлены в таблице 10.7:

Таблица 10.7

№ испытуемых	1 ГРУППА	2 ГРУППА	3 ГРУППА

Вычисляем среднее каждого столбца.

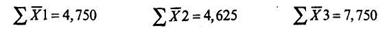
Вычисляем размах (max—min) в каждом столбце: это разность между наибольшим и наименьшим значением.

1 гр 9-2 = 7

2 гр 8-2 = 6

3 гр 10-6 = 4

Вычисляем разность между максимальным и минимальным средним:

(max XI - min X2)= 7,750 - 4,625

Формула для подсчета эмпирического значения критерия очень проста:

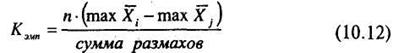
В нашем случае n = 8 и сумма размахов равна 7 + 6 + 4 = 17. Подставляем эти величины в формулу (10.12), получаем:

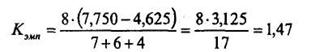
По таблице 18 Приложения 1 находим К_кр при n = 8 и k= 3

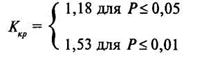
Строим «ось значимости»:

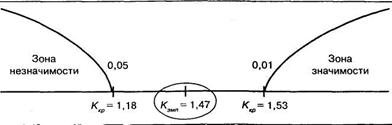
Таким образом, на уровне 5% можно принять гипотезу H₁ о том, что различия между выборками не случайны и обусловлены действием регулируемого фактора. Важно подчеркнуть, что и однофакторный дисперсионный анализ привел бы к тому же выводу (величина F = 6,05 при уровне значимости Р = 0,008).

С помощью этого критерия можно также статистически обосновано высказать утверждение о равенстве или неравенстве полученных средних. Проверка осуществляется по формуле:

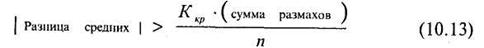
в том случае, если неравенство выполняется, то различия между средними статистически значимы. Разница средних берется по модулю.

С помощью формулы (10.13) сравним средние задачи 10.4:

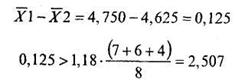
Неравенство не выполняется, следовательно, статистически значимых различий между значениями первого и второго среднего нет.

Проверим различия между первым и третьим значениями среднего:

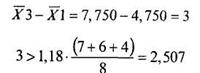
В данном случае неравенство выполняется. Проверим различия между вторым и третьим значениями среднего:

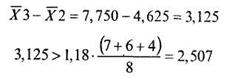
И здесь неравенство выполняется. Таким образом, мы можем окончательно сказать, что в нашем случае справедливо: X1 = X2 ≠ X3. Из этого следует, что средний показатель количества решенных задач достоверно выше у учащихся интерната и колледжа.

Критерий Немени

Этот критерий основан на ранжировании всей выборки. Если в выборке к групп по п элементов в каждой, то наименьшему наблюдению приписывается ранг 1, наибольшему ранг n • k. Затем суммируются ранги каждой из групп и вычисляются абсолютные значения их разностей. По таблице 19 Приложения 1 делается вывод об уровне сходства или различия в группах.

Критерий Немени позволяет, так же как и предыдущий критерий, оценить различия средних между группами. Для применения этого критерия необходимо, чтобы группы испытуемых были равными по величине. Количество групп должно быть не меньше трех и не больше 10.

Задача 10.5В четырех группах спортсменов высокой квалификации (футболисты, гимнасты, теннисисты и пловцы, по 5 человек в каждой) сравнивалось время реакции выбора в мс. Психолог выясняет вопрос, будут ли различия по времени реакции у спортсменов разного профиля.

В этой задаче регулируемый фактор (условие) — спортивная специализация; результирующий признак — длительность времени реакции. Гипотеза Н_o констатирует отсутствие различий между группами, а также отсутствие влияния регулируемого фактора, т.е. типа спортивной специализации.

Решение. Результаты эксперимента приведены в таблице 10.8, в которой проведено необходимое ранжирование экспериментальных данных одновременно по всей выборке в целом:

Таблица 10.8

1 группа	2 группа	3 группа	4 группа
Баллы	Ранги	Баллы	Ранги	Баллы	Ранги	Баллы	Ранги
	7,5
			7,5
Сумма рангов по стол­бцам	55,5		70,5

Проверим правильность ранжирования: 55,5 + 70,5 + 51 + 33 = 210

И по формуле (1.2): '

,

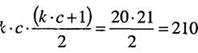где k — число строк, а с — число столбцов.

Абсолютные разности между суммами рангов представим также в виде таблицы:

Таблица 10.9

Разности рангов между группами	1-2	1 -3	1-4
2-3	|55,5- 70,5| = 15	|55,5-51|=4,5	|55,5- 33|=22,5
2-4		|70,5- 51|=19,5	|70,5- 33|=37,5
3-4			|51-33| = 18

По таблице 19 Приложения 1 находим D_кр для k = 4 и п = 5

Строим «ось значимости»:

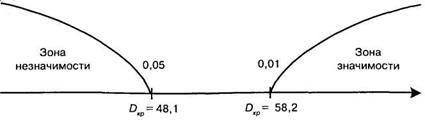
Как видим из таблицы 10.9 для абсолютных разностей рангов ни одна из этих величин не достигает даже 5% уровня значимости. Следовательно, можно с уверенность утверждать, что различия во времени реакции между группами спортсменов высокой квалификации носят случайных характер и тип спортивной специализации не влияет на эти показатели. Подчеркнем, что расчет этих же данных по методу однофакторного дисперсионного анализа также не выявил статистически значимых различий, величина F= 1,7 при уровне значимости Р = 0,206.

Для применения «быстрых» методов — критериев дисперсионного анализа необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отношений.

2. Результативный признак должен быть распределен нормальнов исследуемой выборке.

3.Группы испытуемых должны быть равными по численности.

4. Количество групп должно быть не меньше трех, и в последнем методе не больше 10.

Глава 11 КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

11.1. Понятие корреляционной связи

Психолога нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых группах. Например, могут ли учащиеся с высоким уровнем тревожности демонстрировать стабильные академические достижения, или связана ли продолжительность работы психологов в школе с размером их заработной платы, или с чем больше связан уровень умственного развития учащихся — с их успеваемостью по математике или по литературе и т.п.?

В математике для описания связей между переменными величинами используют понятие функции F, которая ставит в соответствие каждому определенному значению независимой переменной X определенное значение зависимой переменной Y. По­лученная зависимость обозначается как Y= F(X). Здесь X — является аргументом, а Y — соответствующим ему значением функции F(X). Такого рода однозначные зависимости между переменными величинами Х и Y называют функциональными. Хорошо известен пример функциональной зависимости из школьного курса физики — S = V ∙ Т, где S — путь, V— скорость, Т — время. При этом, зная две из переменных величин, всегда можно найти третью.

Но подобные однозначные, или функциональные, связи между переменными величинами встречаются далеко не всегда.

Известно, например, что в среднем между ростом людей и их весом наблюдается положительная связь, и такая, что чем больше рост, тем больше вес человека. Однако из этого правила имеются исключения, когда относительно низкие люди имеют избыточный вес, и, наоборот, астеники, при высоком росте имеют малый вес. Причиной подобных исключений является то, что каждый биологический, физиологический или психологический признак определяется воздействием многих факторов: средовых, генетических, социальных, экологических и т.д. Поэтому связи между психологическими признаками имеют не функциональный, а статистический характер, когда в среднем определенному значению одного признака, например, выраженной акцентуации подростков по гипертимному типу, рассматриваемому в качестве аргумента, соответствует не одно какое-либо значение, а целый спектр, распределяющихся в вариационный ряд числовых значений, например, такого психологического признака, как тревожность, который можно рассматривать в качестве зависимой переменной или функции. Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь — это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.

Функциональные связи легко обнаружить и измерить на единичных и групповых объектах, однако этого нельзя проделать с корреляционными связями, которые можно изучать только на представительных выборках методами математической статистики. Корреляционные связи — это вероятностные изменения. «Оба термина, — пишет Е.В. Сидоренко, — корреляционная связь и корреляционная зависимость — часто используются как синонимы. Между тем, согласованные изменения признаков и отражающая это корреляционная связь между ними может свидетельствовать не о зависимости этих признаков между собой, а о зависимости обоих этих признаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании. Зависимость подразумевает влияние, связь — любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетель ство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказывается за пределами исследуемой пары признаков, нам неизвестно».

Виды корреляционных связей между измеренными признаками могут быть различны: так, корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна — если с увеличением или уменьшением одной переменной X, вторая переменная Y в среднем либо также растет, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами.

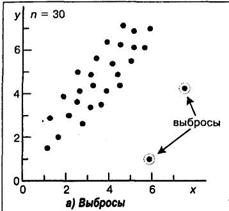
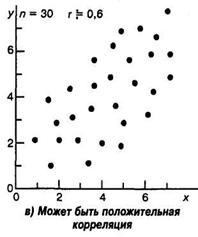
Корреляция будет положительной, если с увеличением переменной X переменная Y в среднем также увеличивается, а если с увеличением X переменная Y имеет в среднем тенденцию к уменьшению, то говорят о наличии отрицательной корреляции. Возможна ситуация, когда между переменными невозможно установить какую-либо зависимость. В этом случае говорят об отсутствии корреляционной связи. Подчеркнем, однако, что нередко встречаются задачи, в которых традиционная и наиболее часто встречающаяся в психологических исследованиях линейная корреляционная связь отсутствует, в то время как имеется высокозначимая криволинейная связь, например, полиномиальная или гиперболическая.

.

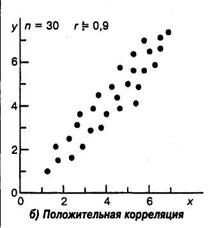
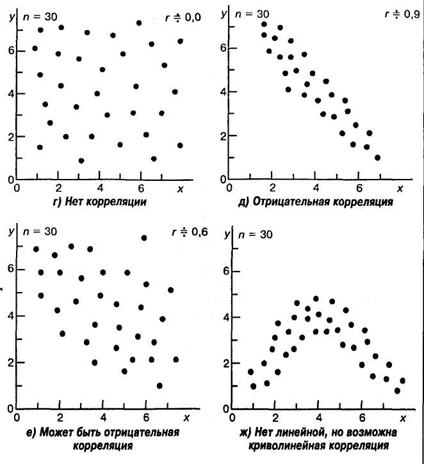
Рис. 3. Типы корреляционных связей

Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.

Зависимость между коррелирующими переменными X и Y, как и в математике, можно выразить с помощью формул и уравнений (т.е. аналитически), а можно выразить графически.

Графики корреляционных зависимостей строят по уравнениям следующих функций: Y_x=F(X) или X_y=F(Y),

которые называются уравнениями регрессии.Здесь Y_x и Х_у так называемые условные средние арифметические переменных Х и Y.

Переменные X и Y могут быть измерены в разных шкалах, именно это определяет выбор соответствующего коэффициента корреляции. Представим соотношения между типами шкал, в которых могут быть измерены переменные Х и Y и соответствующими мерами связи в виде таблицы 11.1:

Таблица 11.1.

Тип шкалы	Мера связи
Переменная X	Переменная Y
Интервальная или отношений	Интервальная или отношений	Коэффициент Пирсона rху
Ранговая, интервальная или отношений	Ранговая, интервальная или отношений	Коэффициент Спирмена ρху
Ранговая	Ранговая	Коэффициент «τ» Кендалла
Дихотомическая	Дихотомическая	Коэффициент «φ»
Дихотомическая	Ранговая	Рангово-бисериальный Rrb
Дихотомическая	Интервальная или отношений	Бисериальный Rбис
Интервальная	Ранговая	Не разработан