Параметрические и непараметрические критерии

Все критерии различий условно подразделены на две группы: параметрические и непараметрические критерии.

Критерий различия называют параметрическим, если он основан на конкретном типе распределения генеральной совокупности (как правило, нормальном) или использует параметры этой совокупности (средние, дисперсии и т.д.). Критерий различия называют непараметрическим, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности. Поэтому для непараметрических критериев предлагается также использовать такой термин как «критерий, свободный от распределения» (8, с. 37).

При нормальном распределении генеральной совокупности параметрические критерии обладают большей мощностью по сравнению с непараметрическими. Иными словами, они способны с большей достоверностью отвергать нулевую гипотезу, если последняя неверна. По этой причине в тех случаях, когда выборки взяты из нормально распределенных генеральных совокупностей, следует отдавать предпочтение параметрическим критериям.

Однако, как показывает практика, подавляющее большинство данных, получаемых в психологических экспериментах, не распределены нормально, поэтому применение параметрических критериев при анализе результатов психологических исследований может привести к ошибкам в статистических выводах. В таких случаях непараметрические критерии оказываются более мощными, т.е. способными с большей достоверностью отвергать нулевую гипотезу.

Итак, при оценке различий в распределениях, далеких от нормального, непараметрические критерии могут выявить значимые различия, в то время как параметрические критерии таких различий не обнаружат. Важно отметить, что, во-первых, непараметрические критерии выявляют значимые различия и в том случае, если распределение близко к нормальному, во-вторых, при вычислениях вручную непараметрические критерии являются значительно менее трудоемкими, чем параметрические.

6.1.2. Рекомендации к выбору критерия различий

При подготовке экспериментального исследования психолог должен заранее запланировать характеристики сопоставляемых выборок (прежде всего связность — несвязность и однородность), их величину (объем), тип измерительной шкалы и вид используемого критерия различий. Последовательно это можно представить в виде следующих этапов:

o Прежде всего, следует определить, является ли выборка связной (зависимой) или несвязной (независимой).

o Следует определить однородность — неоднородность выборки.

o Затем следует оценить объем выборки и, зная ограничения каждого критерия по объему, выбрать соответствующий критерий.

o При этом целесообразнее всего начинать работу с выборанаименее трудоемкого критерия.

o Если используемый критерий не выявил различия — следует применить более мощный, но одновременно и болеетрудоемкий критерий.

o Если в распоряжении психолога имеется несколько критериев, то следует выбирать те из них, которые наиболее полно используют информацию, содержащуюся в экспериментальных данных.

o При малом объеме выборки следует увеличивать величину уровня значимости (не менее 1%), так как небольшая выборка и низкий уровень значимости приводят к увеличению вероятности принятия ошибочных решений.

Непараметрические критерии для связных выборок

Критерий знаков G

Нередко, сравнивая «на глазок» результаты «до» и «после» какого либо воздействия (например, тренинга), психолог видит тенденции повторного измерения — большинство показателей может увеличиваться или, напротив, уменьшаться. Наиболее простым путем оценки различий, казалось бы, является подсчет процентов в изменениях в ту или другую сторону «до» и «после» и сравнение полученных процентов между собой. На основе этого сравнения можно было бы придти к заключению, что если наблюдаются различия в процентах, то имеет место различие и в сравниваемых психологических характеристиках «до» и «после». Подобный подход категорически неприемлем, поскольку для процентов нельзя определить уровень достоверности в их различиях. Делать какие либо выводы из экспериментального материала возможно только на основе статистических процедур, специально сконструированных так, что на их основе можно определить уровень достоверности различий. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Поэтому, для того чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей.

Для решения подобных статистических задач психолог может использовать целый ряд критериев различия. Один из наиболее простых критериев различия — критерий знаков G. Этот критерий относится к непараметрическим и применяется только для связанных (зависимых) выборок. Он дает возможность установить, насколько однонаправленно изменяются значения признака при повторном измерении связанной, однородной выборки. Критерий знаков применяется к данным, полученным в ранговой, интервальной и шкале отношений.

Решим с использованием критерия знаков следующую задачу.

Задача6.1. Психолог проводит групповой тренинг. Его задача — выяснить будет ли эффективен данный конкретный вариант тренинга для снижения уровня тревожности участников?

Решение. Для решения этой задачи психолог с помощью теста Тейлора дважды выявляет уровень тревожности у 14 участников до и после проведения тренинга. Результаты измерения приведем в таблице 6.1, включив в нее столбец, необходимый для расчета по критерию знаков G.

Таблица 6.1

№ испытуемых п/п	Уровень тревожности «до» тренинга	Уровень тревожности «после» тренинга	Сдвиг
			+4
			-9
			-1
			-6
			+5
			+3
			+1
			+1
			+1
			-1
			-7
			+2
			+3

В столбце, обозначенном словом «Сдвиг», для каждого участника отдельно определяют, насколько изменился его уровень тревожности после проведения тренинга. Сдвиг — это величина разности между уровнями тревожности одного и того же участника «после» и «до» тренинга. Но не наоборот! Величины сдвигов обязательно должны быть даны в соответствующем столбце таблице с учетом знаков.

В критерии знаков по результатам, полученным в столбце таблицы, обозначенном словом «Сдвиг», подсчитываются суммы нулевых, положительных и отрицательных сдвигов. При использовании критерия знаков необходимо учитывать только сумму положительных и отрицательных сдвигов, а сумму нулевых — отбрасывать.

Проведем необходимый подсчет для нашей задачи:

общее число (сумма) нулевых сдвигов = 1;

общее число (сумма) положительных сдвигов = 8;

общее число (сумма) отрицательных сдвигов = 5.

Таким образом, отбросив нулевые сдвиги, получаем 13 ненулевых сдвигов. При этом подсчет показал, что сдвиги имели место и что большая часть из них положительна.

Напомним, что критерий знаков Gпредназначен для установления того, как изменяются значения признака при повторном измерении связной выборки: в сторону увеличения или уменьшения. Поэтому, анализируя соотношение положительных и отрицательных сдвигов в нашей задаче, решаем вопрос: можно ли утверждать, что после проведения тренинга наблюдается достоверный сдвиг в сторону уменьшения уровня тревожности участников?

Для решения этого вопроса необходимо ввести два обозначения. Первое — сумма сдвигов, получившаяся наибольшей носит название типичного сдвигаи обозначается буквой п. Типичный сдвиг используется при работе с таблицей 1 Приложения, в которой приводятся критические величины 5% и 1% уровней значимости данного критерия. Второе — сумма сдвигов, получившаяся наименьшей, носит название — нетипичного сдвигаи обозначается как — G_эмп. Эта величина (G_эмп) располагается на «оси значимости». В нашем случае G_эмп = 5. В целом типичный и нетипичный сдвиги рассматриваются как дополнительные друг к другу.

Подчеркнем, что в том случае, когда величины типичного и нетипичного сдвигов оказываются равными, критерий знаков неприменим.

Оценка статистической достоверности различий по критерию знаков производится по таблице 1 Приложения. В ней в столбце, обозначенным буквой п приведены величины типичных сдвигов, а в столбцах, имеющих обозначение, соответствующее уровнями значимости Р = 0,05 и Р = 0,01, — так называемые критические величины. Условно их также можно считать нетипичными сдвигами. Они обозначаются как G и с ними сравнивается полученное значение нетипичного сдвига G_эмп.

Итак, оцениваем уровень достоверности различий нашей задачи. Для этого необходимо воспользоваться таблицей 1 Приложения. Поскольку в нашем примере п = 8, (это число типичных сдвигов), поэтому нужный нам участок таблицы 1 Приложения выглядит так:

Таблица 6.2

п	Р
0,05	0,01

Более компактно соответствующую строчку таблицы 1 Приложения принято записывать следующим образом:

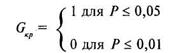
Эта запись означает, что при уровне значимости в 5%, сумма нетипичных сдвигов не должна превышать 1, а при уровне значимости в 1% — 0. В нашем случае G_эмп = 5, что существенно больше 1.

Для большей наглядности следует построить так называемую «ось значимости», на которой располагаются как величины критических сдвигов, так и величина G_эмп, т.е. величина нетипичного сдвига.

«Ось значимости» имеет следующий вид:

Использование «оси значимости» позволяет отчетливо видеть, что G_эмп попало в зону незначимости, т.е. полученный в эксперименте общий положительный сдвиг, который соответствует увеличению уровня тревожности испытуемых после проведения тренинга, статистически недостоверен. Иначе говоря, данный способ воздействия не привел к существенным изменениям в уровне тревожности испытуемых.

Обращаем внимание читателя, что в критерии знаков «ось значимости» образно говоря, перевернута. Нуль располагается не как обычно (на числовой оси слева), а справа и увеличение числового ряда идет в противоположную сторону, т.е. справа налево. Последнее связано с тем, что чем больше количество нетипичных сдвигов, тем меньше вероятность того, что суммарный сдвиг окажется статистически достоверен. Подобные исключения в направленности «оси значимости» будут встречаться и далее. Такой тип расположения «оси значимости» справедлив для критериев Т — Вилкоксона,-Макнамары и критерия U – Вилкоксона —Манна—Уитни.

Полученный выше результат может быть переформулирован также в терминах нулевой и альтернативной гипотез: поскольку преобладание типичного положительного направления сдвига в данном конкретном эксперименте является случайным, то должна быть принята гипотеза H₀ об отсутствии различий, или о наличии сходства. Возвращаясь к психологической задаче, укажем, что, согласно критерию знаков, примененный психологом способ тренинга неудовлетворителен, поскольку не дает статистически достоверных изменений в состоянии участников тренинга.

Задача6.2. Получив отрицательный результат, психолог внес в способ тренинга соответствующие коррективы. Он снова выдвигает гипотезу: улучшенный способ тренинга позволяет эффективно снижать уровень тревожности испытуемых.

Решение. Для проверки этого утверждения психолог провел аналогичный, эксперимент, но уже на большей выборке испытуемых. На это раз он включил в группу 19 человек. В таблице 6.3 приводятся результаты эксперимента:

Таблица 6.3

№ испытуемых п/п	Уровень тревожности «до» тренинга	Уровень тревожности «после» тренинга	Сдвиг
			-2
			- 17
			+ 1
			-8
			- 11
			-20
			- 18
			-3
			- 3
			- 12
			- 1
			-2
			-6
			- 14
			- 1
			+ 2

Подсчитываем суммы сдвигов: нулевых – 3; положительных - 2; отрицательных - 14

Таким образом, получаем, что большинство сдвигов отрицательны. Теперь именно отрицательные сдвиги будут «типичными» в отличие от предыдущего случая, когда типичными были положительные сдвиги. В таблице 1 Приложения ищем строчку, в которой п = 14. Эта строчка вынесена ниже в таблицу 6.4:

Таблица 6.4

п	Р
0,05	0,01

Поскольку в нашем случае основной, типичный сдвиг — отрицательный, то дополнительный, «нетипичный» сдвиг будет положительным и, как следует из таблицы 6.4, на уровне значимости 5% общее количество таких сдвигов не должно превышать числа 3, а при уровне значимости 1% — 2. Вновь переведем вышесказанное в стандартную форму записи:

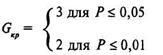
В нашем случае сумма положительных (т.е. нетипичных) сдвигов равна 2. То есть G_эмп = 2. Строим «ось значимости»:

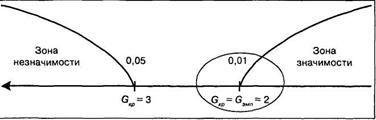
Значение G_эмп = 2 совпало с критическим значением зоны значимости G_кр для 1%. Следовательно, психолог может утверждать, что полученный в результате эксперимента сдвиг уровня тревожности статистически значим на 1% уровне. Иными словами, в результате тренинга тревожность испытуемых понизилась статистически достоверно.

Переформулируем полученньщ результат в терминах статистических гипотез: поскольку преобладание типичного отрицательного направления сдвига в данном случае не случайно, то, следовательно, на 1 % уровне может быть принята гипотеза H₁ о наличии различий, а гипотеза H_о о сходстве отклонена.

Для лучшего понимания работы с критерием знаков рассмотрим последнюю строчку таблицы 1 Приложения. В ней стоит число 300, это означает, что для работы с очень большими по численности выборками критерий знаков не предназначен. При числе типичных сдвигов, равном 300, критические значения для нетипичных сдвигов будут равны соответственно:

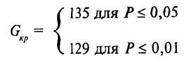
Следовательно, если число нетипичных сдвигов G_’эмп при числе типичных сдвигов равном 300 не превышает 135 (G_’эмп < G_’кр = 135), то на уровне значимости 5% принимается гипотеза Н₁ о различии; и, аналогично: если G_эмпI не превышает 129 (G_’эмп < G_’кр = 129), то на 1% уровне значимости также принимается гипотеза H₁ о различии и на соответствующих уровнях отклоняются гипотезы H_о о сходстве. Мы помним, что при работе с критерием знаков сумма нулевых сдвигов не учитывается. Поэтому общая величина выборки в этом критерии может быть достаточно большой, но не большей чем 300 + 135 = 435 элементов. Напомним еще раз, что в случае равенства числа типичных и нетипичных сдвигов — критерий знаков не применим.

В заключении следует заметить, что критерий знаков является одним из самых простых по способу вычисления. Традиционно он считается одним из наименее мощных. Однако можно утверждать, что если критерий знаков показал значимые различия на 1% уровне, то другие, более мощные критерии подтвердят эти различия. В то же время, если критерий знаков не выявил значимых различий, возможно, что более мощные критерии, напротив, такое различие выявят.

Для применения критерия Gнеобходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале порядка, интервалов и отношений.

2. Выборка должна быть однородной и связной.

3. Число элементов в сравниваемых выборках должно быть равным.

4. G критерий знаков может применяться при величине типичного сдвига от 5 до 300 (на большую величину не рассчитана таблица достоверности).

5. При большом числе сравниваемых парных значений критерий знаков достаточно эффективен.

6. При равенстве типичных и нетипичных сдвигов критерий знаков неприменим, следует использовать другие критерии.