Колебания пакета лопаток постоянного профиля

Турбинных ступеней

Колебания рабочих лопаток

Основными источниками возбуждения переменных во времени нагрузок в рабочих лопатках являются:

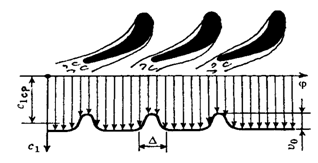
- кромочные следы за сопловой решеткой ступени (рис. 24.1,а);

- нестационарные волновые явления в виде скачков уплотнения (рис. 24.1,в).

- технологические отклонения при изготовлении диафрагм;

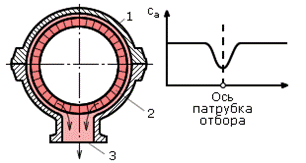
- неравномерность поля скоростей из-за наличия патрубков отбора пара (рис. 24.1,б);

- парциальный подвод водяного пара;

- вибрация ротора;

- задевания в различного рода уплотнений;

- формирование отрывных зон в проточной части турбины;

а) б)

Рис.24.1. Формирование кромочных следов и неравномерности поля скоростей за сопловой

решеткой турбинной ступени (а) и неравномерности скорости потока из-за наличия патрубка отбора 3 (б)

Данные источники возбуждающих сил вызывают вынужденные колебания венцов рабочих лопаток. Если лопатку, жестко закрепленную в корне, вывести из состояния равновесия, то она будет совершать колебания с различными формами линии прогиба, которых может быть бесконечное множество. На рис. 24.2 показаны три главные формы колебаний, каждой из которых соответствует определенная собственная частота. В зависимости от уровня демпфирования возмущающей силы амплитуда колебаний А приобретает различные значения (рис. 24.3). В случае совпадения частоты возмущающей силы и частоты собственных колебаний возникает явление резонанса, при котором динамические напряжения в лопатке растут кризисным образом и могут достигать опасных значений.

Главной задачей расчета колебаний рабочих лопаток является определение их собственных частот, форм колебаний и напряжений. Рассмотрим случай, когда поперечные смещения каждого сечения лопатки малы по сравнению с ее длиной. Тогда можно принять систему координат, показанную на рис. 24.4.

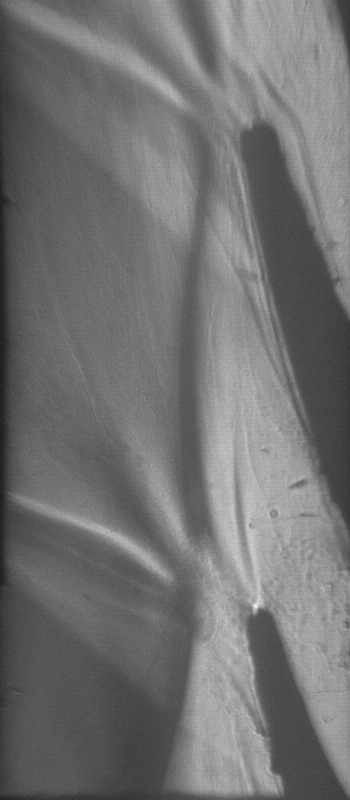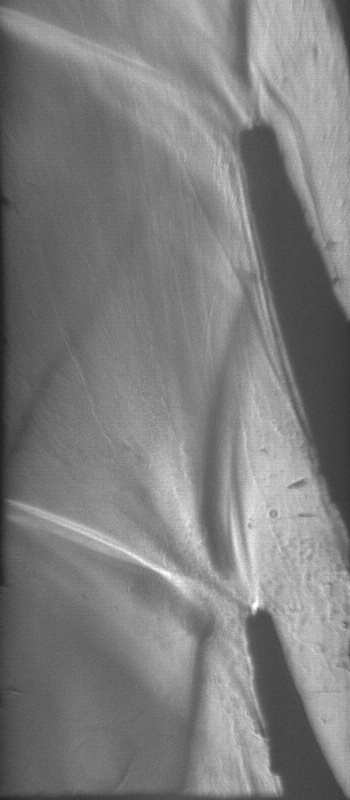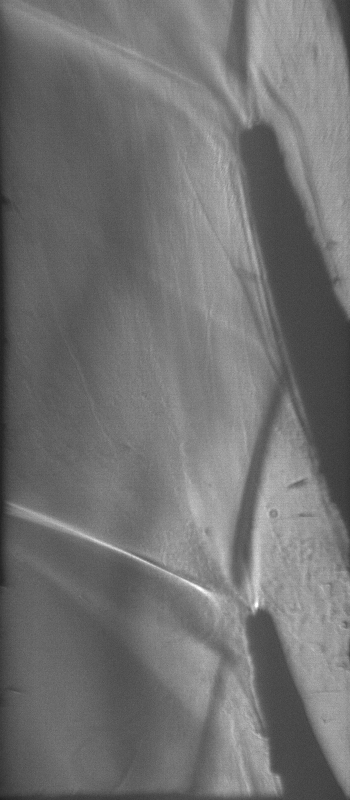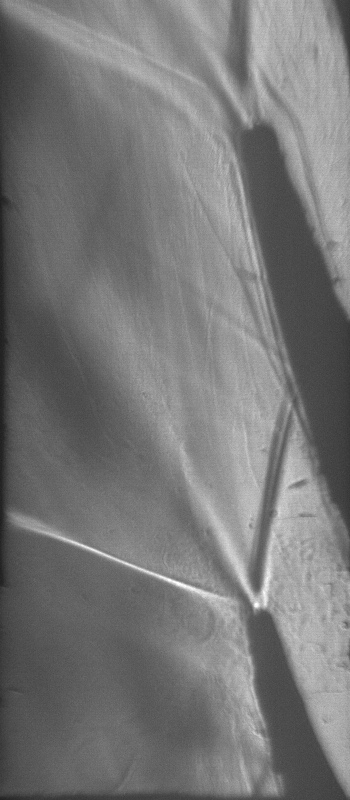
Рис. 24.1, в. Волновая структура потока в косом срезе сопловой решетки

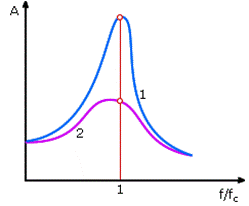
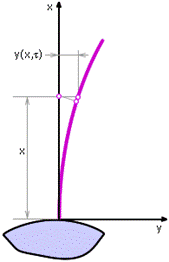
Рис. 24.2. Главные формы колебаний лопатки со свободным венцом

Рис. 24.3. Зависимость амплитуды колебаний А от частоты возмущающей силы с малым (1) и большим (2) демпфированием (f_с – одна из собственных частот колебаний лопатки)

Рис. 24.4. Координаты изогнутой (упругой) оси рабочей лопатки

Отклонения точек упругой оси лопатки при поперечных колебаниях зависят от координаты х и от времени t: y=y(x, t). Введем следующие обозначения: m(х)=rF_x - погонной массы рабочей лопатки с плотностью r металла и площадью поперечного сечения F_x; J(х) - момента инерции поперечного сечения относительно его нейтральной оси, расположенной перпендикулярно плоскости колебаний; q(х) – распределенной по длине лопатки внешней нагрузки; Е – модуля упругости. Тогда поперечные перемещения упругой оси y в разных точках хсвязаны со временем t уравнением

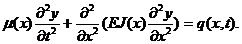(24.1)

В данном линейном уравнении четвертого порядка первый член характеризует силы инерции, формирующиеся при перемещении лопатки в направлении y с ускорением 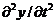. Второй член определяется силами упругого сопротивления материала лопатки при ее прогибе y. Третий член представляет собой силу сопротивления поперечным перемещениям лопатки при воздействии внешней нагрузки q(х).

В итоге преобразований, которые здесь не представлены, можно получить формулу для определения собственной частоты колебаний на основе известных корней уравнения (9.1).

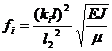(24.2)

При этом первым трем формам колебаний единичной рабочей лопатки длиной l₂, представленным на рис. 24.2, соответствуют следующие значения k_il₂:

k₁l₂=1,875; k₂l₂=4,694; k₃l₂=7,855.

Поскольку в реальных условиях из-за упругости заделки хвостовика лопатки, а также неточностей в формулировке задачи, значения частот колебаний оказываются ниже рассчитываемых по (24.1), то в практических расчетах используют поправочный коэффициент y=f_дейст/f_расч, значения которого получают из экспериментальных исследований. Изменение этого коэффициента для первого тона колебаний в зависимости от гибкости лопатки l=l₂/i (i=(J_x/F_x)^0,5 - радиус инерции поперечного сечения лопатки) показано на рис. 24.5 (для второго и третьего тонов колебаний y = 1). Тогда действительные частоты колебаний одиночной лопатки постоянного по ее высоте профиля (F_x=F) определяются по формуле:

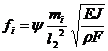. (24.3)

В формуле (24.3) значения m_i для первых трех тонов колебаний следующие: первого тона m₁=0,56;второго- m₂=3,51,третьего- m₃=9,82. Получаемые при этом значения частот колебаний единичной лопатки определяются в условиях не вращающегося ротора турбины (n=0).

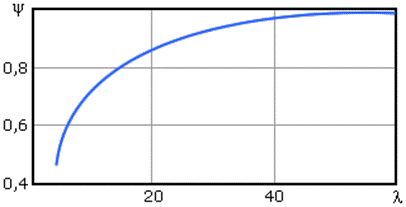
Рис. 24.5. Зависимость множителя y от гибкости лопатки l=l₂/i

Рис.24.6. Формы колебаний пакета лопаток

Для определения частот колебаний пакета лопаток в формулу (24.3) вводится множитель j_i = f_ст.п.i/f_ст.1, учитывающий влияние жесткости и массы бандажной ленты. Его значение находится по зависимости, представленной на рис. 24.7, где коэффициент жесткости бандажа

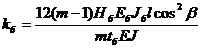. (24.4)

В (24.4) Н_б=0,2…0,3, если бандаж приклепан к перу лопаток; Н_б=0,8…1,0, если он припаян; если приварен Н_б=1,0. Е_б, J_б, t_б – соответственно, модуль упругости, момент инерции и длина бандажа, приходящаяся на одну лопатку (шаг бандажа); b - угол между направлением вращения диска и нормалью к плоскости минимальной жесткости лопатки (β = 90 - β_уст); n_б=m_б/m_l – отношение массы бандажа, приходящей на одну лопатку, к массе лопатки m_l. В итоге частота колебаний пакета лопаток, например, для тона колебаний А₀:

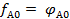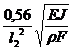y . (24.5)

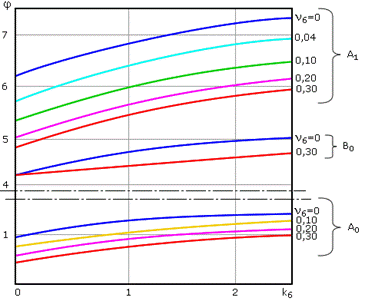
Рис. 24.7. Зависимость множителя j от коэффициента жесткости бандажа k_б и

его относительной массы n_б

Обратите внимание, для коэффициента φ_В0 на рис.24.7 изображены две ограничительные линии, между которыми расположены все его значения. Коэффициент массы бандажа не оказывает влияния на частоту колебаний типа В₀, так как вершины лопаток неподвижны.

При жестком присоединении бандажа к лопаткам в процессе вращения ротора турбины происходит некоторое закручивание каждой лопатки в пакете. Тогда формируются формы колебаний пакетов, которые называются изгибно-крутильными (рис. 24.8). Для оценки влияния такой деформации следует учитывать относительную жесткость бандажа при изгибно-крутильных колебаниях. Этот учет осуществляется коэффициентом, значения которого представлены на рис.5.17 книги: А.Г. Костюк. Динамика и прочность турбомашин. – М.: Изд-во МЭИ, 2000.

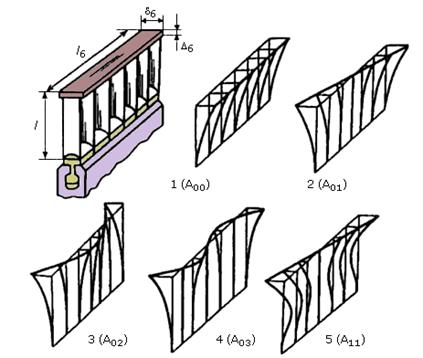
Рис. 24.8. Изгибно-крутильные колебания пакета лопаток

Рис. 24.9. Вибрационная (резонансная) диаграмма для лопаточного аппарата

Турбинных ступеней

Колебания рабочих лопаток

Основными источниками возбуждения переменных во времени нагрузок в рабочих лопатках являются:

- кромочные следы за сопловой решеткой ступени (рис. 24.1,а);

- нестационарные волновые явления в виде скачков уплотнения (рис. 24.1,в).

- технологические отклонения при изготовлении диафрагм;

- неравномерность поля скоростей из-за наличия патрубков отбора пара (рис. 24.1,б);

- парциальный подвод водяного пара;

- вибрация ротора;

- задевания в различного рода уплотнений;

- формирование отрывных зон в проточной части турбины;

а) б)

Рис.24.1. Формирование кромочных следов и неравномерности поля скоростей за сопловой

решеткой турбинной ступени (а) и неравномерности скорости потока из-за наличия патрубка отбора 3 (б)

Данные источники возбуждающих сил вызывают вынужденные колебания венцов рабочих лопаток. Если лопатку, жестко закрепленную в корне, вывести из состояния равновесия, то она будет совершать колебания с различными формами линии прогиба, которых может быть бесконечное множество. На рис. 24.2 показаны три главные формы колебаний, каждой из которых соответствует определенная собственная частота. В зависимости от уровня демпфирования возмущающей силы амплитуда колебаний А приобретает различные значения (рис. 24.3). В случае совпадения частоты возмущающей силы и частоты собственных колебаний возникает явление резонанса, при котором динамические напряжения в лопатке растут кризисным образом и могут достигать опасных значений.

Главной задачей расчета колебаний рабочих лопаток является определение их собственных частот, форм колебаний и напряжений. Рассмотрим случай, когда поперечные смещения каждого сечения лопатки малы по сравнению с ее длиной. Тогда можно принять систему координат, показанную на рис. 24.4.

Рис. 24.1, в. Волновая структура потока в косом срезе сопловой решетки

Рис. 24.2. Главные формы колебаний лопатки со свободным венцом

Рис. 24.3. Зависимость амплитуды колебаний А от частоты возмущающей силы с малым (1) и большим (2) демпфированием (f_с – одна из собственных частот колебаний лопатки)

Рис. 24.4. Координаты изогнутой (упругой) оси рабочей лопатки

Отклонения точек упругой оси лопатки при поперечных колебаниях зависят от координаты х и от времени t: y=y(x, t). Введем следующие обозначения: m(х)=rF_x - погонной массы рабочей лопатки с плотностью r металла и площадью поперечного сечения F_x; J(х) - момента инерции поперечного сечения относительно его нейтральной оси, расположенной перпендикулярно плоскости колебаний; q(х) – распределенной по длине лопатки внешней нагрузки; Е – модуля упругости. Тогда поперечные перемещения упругой оси y в разных точках хсвязаны со временем t уравнением

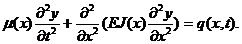(24.1)

В данном линейном уравнении четвертого порядка первый член характеризует силы инерции, формирующиеся при перемещении лопатки в направлении y с ускорением 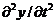. Второй член определяется силами упругого сопротивления материала лопатки при ее прогибе y. Третий член представляет собой силу сопротивления поперечным перемещениям лопатки при воздействии внешней нагрузки q(х).

В итоге преобразований, которые здесь не представлены, можно получить формулу для определения собственной частоты колебаний на основе известных корней уравнения (9.1).

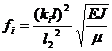(24.2)

При этом первым трем формам колебаний единичной рабочей лопатки длиной l₂, представленным на рис. 24.2, соответствуют следующие значения k_il₂:

k₁l₂=1,875; k₂l₂=4,694; k₃l₂=7,855.

Поскольку в реальных условиях из-за упругости заделки хвостовика лопатки, а также неточностей в формулировке задачи, значения частот колебаний оказываются ниже рассчитываемых по (24.1), то в практических расчетах используют поправочный коэффициент y=f_дейст/f_расч, значения которого получают из экспериментальных исследований. Изменение этого коэффициента для первого тона колебаний в зависимости от гибкости лопатки l=l₂/i (i=(J_x/F_x)^0,5 - радиус инерции поперечного сечения лопатки) показано на рис. 24.5 (для второго и третьего тонов колебаний y = 1). Тогда действительные частоты колебаний одиночной лопатки постоянного по ее высоте профиля (F_x=F) определяются по формуле:

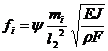. (24.3)

В формуле (24.3) значения m_i для первых трех тонов колебаний следующие: первого тона m₁=0,56;второго- m₂=3,51,третьего- m₃=9,82. Получаемые при этом значения частот колебаний единичной лопатки определяются в условиях не вращающегося ротора турбины (n=0).

Рис. 24.5. Зависимость множителя y от гибкости лопатки l=l₂/i

Колебания пакета лопаток постоянного профиля

Для уменьшения динамических усилий, действующих на колеблющиеся лопатки, их связывают бандажной лентой в пакеты. Пакетирование делает частоты и формы колебаний отдельных лопаток взаимосвязанными. Все формы колебаний лопаток, соединенных бандажом, разделяются на два типа: тип А, когда все лопатки колеблются в одной фазе, и тип В (внутрипакетный тип колебаний), когда не все лопатки колеблются в одной фазе (рис.24.6). Тон колебаний обозначается с индексом, равным числу узлов на упругой линии лопаток. Например, первый тон колебаний А₀, а второй – А₁.

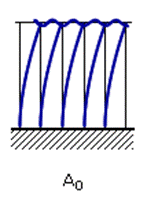
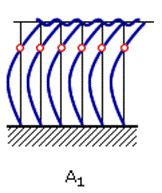
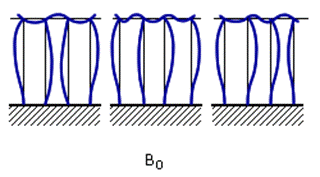
Рис.24.6. Формы колебаний пакета лопаток

Для определения частот колебаний пакета лопаток в формулу (24.3) вводится множитель j_i = f_ст.п.i/f_ст.1, учитывающий влияние жесткости и массы бандажной ленты. Его значение находится по зависимости, представленной на рис. 24.7, где коэффициент жесткости бандажа

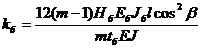. (24.4)

В (24.4) Н_б=0,2…0,3, если бандаж приклепан к перу лопаток; Н_б=0,8…1,0, если он припаян; если приварен Н_б=1,0. Е_б, J_б, t_б – соответственно, модуль упругости, момент инерции и длина бандажа, приходящаяся на одну лопатку (шаг бандажа); b - угол между направлением вращения диска и нормалью к плоскости минимальной жесткости лопатки (β = 90 - β_уст); n_б=m_б/m_l – отношение массы бандажа, приходящей на одну лопатку, к массе лопатки m_l. В итоге частота колебаний пакета лопаток, например, для тона колебаний А₀:

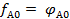y 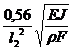. (24.5)

Рис. 24.7. Зависимость множителя j от коэффициента жесткости бандажа k_б и

его относительной массы n_б

Обратите внимание, для коэффициента φ_В0 на рис.24.7 изображены две ограничительные линии, между которыми расположены все его значения. Коэффициент массы бандажа не оказывает влияния на частоту колебаний типа В₀, так как вершины лопаток неподвижны.

При жестком присоединении бандажа к лопаткам в процессе вращения ротора турбины происходит некоторое закручивание каждой лопатки в пакете. Тогда формируются формы колебаний пакетов, которые называются изгибно-крутильными (рис. 24.8). Для оценки влияния такой деформации следует учитывать относительную жесткость бандажа при изгибно-крутильных колебаниях. Этот учет осуществляется коэффициентом, значения которого представлены на рис.5.17 книги: А.Г. Костюк. Динамика и прочность турбомашин. – М.: Изд-во МЭИ, 2000.

Рис. 24.8. Изгибно-крутильные колебания пакета лопаток