Районная олимпиада по математике. 2015 год. 6 класс.
В каждой из предложенных вам задач нужно написать правильный ответв указанном месте. В некоторых задачах может быть несколько ответов. В этом случае для получения полного балла за задачу вам необходимо указать их все. Если вы хотите исправить свой ответ, следует перечеркнуть ранее написанный и рядом написать новый. Никаких решений задач писать не нужно!
Задача 1. Коля старше Кати ровно на один год без одного дня. Коля родился 1 января 2003 года. Когда родилась Катя? (Укажите и год, и число).
Ответ: _____________________________________________________
Задача 2. Старому дедушке Кариму нужно перенести с огорода в сарай 84 мешка с картошкой. Он позвал на помощь внуков. Внуки разбились на пары, и каждой паре досталось по три мешка. Сколько внуков у дедушки Карима?
Ответ: _____________________________________________________
Задача 3. Найдите последнюю цифру числа
N =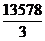 
+ 
+ 
+ 
+ 
.
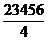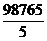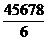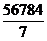Ответ: _____________________________________________________
Задача 4. Храбрый портняжка вырезал из шелка большой квадрат и положил его в сундук. Пришел первый великан, достал квадрат, разрезал его на четыре квадрата и положил все четыре снова в сундук. Потом пришел второй великан, достал один из квадратов, разрезал его на четыре квадрата и положил все четыре снова в сундук. Потом пришел третий великан. И он достал один из квадратов, разрезал его на четыре квадрата и положил все четыре снова в сундук. То же самое проделали все остальные великаны. Сколько квадратов лежало в сундуке после того, как ушел седьмой великан?
Ответ: _____________________________________________________
Задача 5. На конкурсе по истории участникам было задано 12 вопросов. За каждый верный ответ засчитывалось 5 очков, а за каждый неверный снималось 2 очка. Дина получила 39 очков. Сколько из ее двенадцати ответов оказались ошибочными?
Ответ: _____________________________________________________
Задача 6. Фигуры P, Q, R и S — квадраты. Периметр квадрата P равен 12 м, а периметр квадрата Q равен 28 м. Чему равен периметр квадрата S? Ответ укажите в метрах.
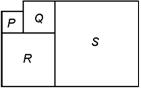
Ответ: _____________________________________________________
Задача 7. Опытный дрессировщик может вымыть слона за 40 минут, а его сыну для этого требуется 2 часа. За какое время они вымоют трех слонов, работая вдвоем? Ответ укажите в минутах.
Ответ: _____________________________________________________
Задача 8. Камиль выписал все трехзначные числа, произведение цифр которых равно 24. Сколько чисел выписал Камиль?
Ответ: _____________________________________________________
Задача 9. Некоторое целое число при делении на 4 дает остаток 1, а при делении на 3 дает остаток 2. Какой остаток может получиться при делении этого числа на 6?
Ответ: _____________________________________________________
Задача 10. На нижней грани кубика нарисованы 6 точек, на левой – 4 и на задней – 2. Какое наибольшее количество точек можно увидеть одновременно, поворачивая этот кубик в руках?
Ответ: _____________________________________________________
Задача 11. Найдите наименьшее четырехзначное число, все цифры которого различны и не равны нулю, такое, что сумма всех его цифр делится на каждую из них.
Ответ: _____________________________________________________
Задача 12. Выполняя домашнее задание по арифметике, Тимур одновременно смотрел телевизор, и вместо того, чтобы прибавить к числу 17 и поделить результат на 5, он вычел из числа 17 и умножил результат на 5. Как ни странно, полученное число совпало с ответом в задачнике. Каким было первоначальное число?
Ответ: _____________________________________________________
Задача 13. Разрежьте фигуру на рисунке на три равные части (не обязательно по линиям сетки). Равными называются части, которые можно совместить, наложив друг на друга. При этом части можно поворачивать и переворачивать. (Даже если вы придумали несколько решений, достаточно указать одно). Ответ изобразите на рисунке. Три картинки даны вам для того, чтобы вы могли исправить неверный ответ в случае необходимости.
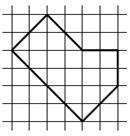
Задача 14. На острове рыцарей и лжецов (рыцари всегда говорят правду, лжецы всегда лгут) встретились 10 человек. Один сказал: «Среди нас ровно один лжец». Другой: «Среди нас ровно два лжеца». И так далее, десятый сказал: «Среди нас ровно десять лжецов». Какое наибольшее количество рыцарей могло быть в этой компании?
Ответ: _____________________________________________________
Задача 15. На уроке физкультуры весь класс выстроился в линейку. По команде учителя каждый четвертый сделал шаг вперед. По второй команде каждый третий из оставшихся сделал шаг назад. После этого на месте остались 14 учеников. Сколько всего учеников могло быть в этом классе? Требуется найти все ответы.
Ответ: _____________________________________________________
Задача 16. Сколько различных результатов можно получить, складывая по два различных числа из набора 1, 2, 3, …, 2015?
Ответ: _____________________________________________________
Задача 17. Пять шахматистов играют турнир в один круг (каждый должен сыграть с каждым по одному разу). В какой-то момент главный судья заметил, что первый шахматист сыграл одну партию, второй — две, третий — три, а четвертый — четыре. Какое наименьшее количество партий мог сыграть к этому времени пятый шахматист?
Ответ: _____________________________________________________
Задача 18. Во втором туре школьной олимпиады по математике участникам было предложено 3 задачи. Первую задачу решили 15 участников, вторую — 13 участников, а третью — 11 участников. И первая и вторая задачи оказались решенными у 8 участников, и первая и третья — у 7 участников, а и вторая и третья — у 6 участников. Все три задачи оказались решенными у 5 участников. Сколько всего школьников приняло участие во втором туре олимпиады?
Ответ: _____________________________________________________
Задача 19. Автомобиль первую половину пути ехал со скоростью 50 км/ч, а вторую половину — со скоростью 70 км/ч. Какова была его средняя скорость?
Ответ: _____________________________________________________
Задача 20. Какой цифрой заканчивается число 22 + 2222 + 222222 ?
Ответ: _____________________________________________________