Районная олимпиада по математике. 2015 год. 5 класс.

В каждой из предложенных вам задач нужно написать правильный ответв указанном месте. В некоторых задачах может быть несколько ответов. В этом случае для получения полного балла за задачу вам необходимо указать их все. Если вы хотите исправить свой ответ, следует перечеркнуть ранее написанный и рядом написать новый. Никаких решений задач писать не нужно!

Задача 1. На доске написали подряд идущие числа: 451, 452, 453, ..., 2015. Сколько чисел написали на доске?

Ответ: _____________________________________________________

Задача 2. Гарри Поттер делает зелье, в которое нужно добавить 3 части лягушачьих лапок, 4 части сушёных грибов, 2 части волчьих ягод и 6 частей воды. Сколько стаканов сушёных грибов ему нужно взять для того, чтобы получить 45 стаканов зелья?

Ответ: _____________________________________________________

Задача 3. Малинкины Наташа и Петя пришли в гости к Клубничкиным Диме и Свете. Им дали угощение: печенье, торт, шоколад и яблоки. Девочки ели печенье и яблоки, а Малинкины – печенье и шоколад. Всё угощение съели. Кто что ел, если каждый ел что-то одно?

Ответ: _____________________________________________________

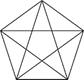Задача 4. Сколько треугольников изображено на рисунке?

Ответ: __________________________________________________

Задача 5. Старому дедушке Кариму нужно перенести с огорода в сарай 72 мешка с картошкой. Он позвал на помощь внуков. Внуки разбились на пары, и каждой паре досталось по три мешка. Сколько внуков у дедушки Карима?

Ответ: _____________________________________________________

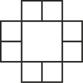
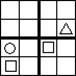Задача 6. Заполните пустые клетки фигурами 4 видов так, чтобы в каждой строке и каждом столбце, а также в каждом отделённом жирными границами квадратике было ровно по одной фигуре каждого вида. (четвёртый вид фигур можно придумать самостоятельно, так как он не задан в условии). Ответ изобразите на рисунке. Три картинки даны вам для того, чтобы вы могли исправить неверный ответ в случае необходимости.

Ответ: ____ ____ ____ __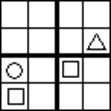

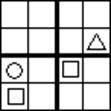Задача 7. Заяц соревновался с черепахой в беге на 100 метров. Когда заяц прибежал к финишу, черепахе оставалось до него еще 80 метров. На сколько метров надо отодвинуть назад стартовую линию для зайца, чтобы при новой попытке оба бегуна пришли к финишу одновременно?

Ответ: _____________________________________________________

Задача 8. На сколько нулей оканчивается произведение 1·2·3·4·…·125?

Ответ: _____________________________________________________

Задача 9. Сколько среди натуральных чисел от 1 до 2015 (включительно) таких, у которых сумма цифр чётна?

Ответ: _____________________________________________________

Задача 10. Фигуры P, Q, R и S – квадраты. Периметр квадрата P равен 8 м, а периметр квадрата Q равен 20 м. Чему равен периметр квадрата S?

Ответ: _____________________________________________________

Задача 11. Учащиеся 4 и 5 классов пошли на экскурсию. Мальчиков было 23, всех пятиклассников – 29, девочек из четвертого класса столько же, сколько мальчиков из пятого. Сколько всего детей побывали на экскурсии?

Ответ: _____________________________________________________

Задача 12. Расставьте знаки арифметических действий и скобки в выражении:5 5 5 5 5 так, чтобы в результате получилось число 13.

Ответ: _____________________________________________________

Задача 13. Найдите наибольшее число, в котором цифры не повторяются и из которого нельзя с помощью вычеркивания одной цифры получить число, делящееся на 5.

Ответ: _____________________________________________________

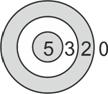
Задача 14. В мишени есть три области, попадание в которых ценится в 5 очков, 3 очка и 2 очка (см. рисунок). Попадание вне этих областей не дает очков. За один раунд игрок делает три выстрела, очки за которые суммируются. За какое минимальное количество раундов можно набрать ровно 119 очков?

Ответ: _____________________________________________________

Задача 15. На острове живут лжецы и рыцари. Однажды 12 человек, собравшиеся в компанию, сделали следующее заявление. Двое сказали: «Ровно двое из здесь присутствующих - лжецы», еще четверо сказали: «Ровно четверо из здесь присутствующих - лжецы», последние шестеро сказали: «Ровно шестеро из здесь присутствующих - лжецы». Сколько лжецов могло быть в этой компании? Укажите все возможные варианты.

Ответ: _____________________________________________________

Задача 16. Разрежьте фигуру по сторонам клеток на две одинаковые по форме и размерам части. Ответ изобразите на рисунке. Три картинки даны вам для того, чтобы вы могли исправить неверный ответ в случае необходимости.

Ответ: ____ _____ _____ ____

Задача 17. Дан квадрат 7 × 7 клеток. Поставьте в некоторых его клетках плюсы так, чтобы в каждом квадрате 3 × 3 было по два плюса.

Ответ: _____________________________________________________

Задача 18. Найдите площадь фигуры, составленной из девяти квадратов, если периметр этой фигуры равен 48 см.

Ответ: _____________________________________________________

Задача 19. Сколько различных результатов можно получить, складывая по два различных числа из набора 1, 2, 3, …, 1000?

Ответ: _____________________________________________________

Задача 20. Во втором туре школьной олимпиады по математике участникам было предложено 3 задачи. Первую задачу решили 13 участников, вторую — 11 участников, а третью — 10 участников. И первая и вторая задачи оказались решенными у 6 участников, и первая и третья — у 7 участников, а и вторая и третья — у 5 участников. Все три задачи оказались решенными у 3 участников. Сколько всего школьников приняло участие во втором туре олимпиады?

Ответ: _____________________________________________________________________