Понятие теоремы. Необходимое и достаточное условия

Теорема– это высказывание при изучении какой-либо теории, требующее доказательства или какого-нибудь (то есть истинное в данной теории). Доказательство опирается на аксиомы данной теории, определения и другие теоремы, которые уже доказаны.

При записи любой теоремы выделяется разъяснительная часть, условие и заключение. Теорему можно рассматривать как импликацию: (…) А 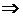В «из А следует В». Здесь: A – условие, а В — заключение или вывод теоремы, а многоточие содержит разъяснительную часть теоремы, в которой указываются дополнительные свойства объектов. Такая теорема называется прямой. В ней А называют достаточным условием для В, а В называют необходимым условием для А.

Прямую теорему можно сформулировать следующими способами:

1) если верно А, то верно и В;

2) для справедливости В достаточно, чтобы выполнялось А;

3) для справедливости А необходимо, чтобы выполнялось В.

В любой теории можно сформулировать четыре вида теорем:

1. Из А следует В — прямая терема: А 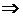В.

2. Из В следует А – обратная теорема: В 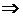А.

3. Из не А следует не В – противоположная теорема: .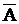

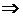
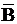4. Из не В следует не А – обратная противоположной теорема: .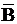

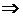
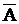Прямая и обратная теоремы связаны с понятиями необходимого и достаточного условий. Условие в прямой теореме становится выводом или заключением для обратной. А вывод в прямой теореме становится условием для обратной. Если теорема формулируется как эквивалентность: 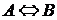, то А называют необходимым и достаточным условием для В. При доказательстве необходимого условия в теореме, из истинности условия А требуется определить истинность В: 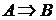. При доказательстве достаточного условия в теореме, из истинности заключения В требуется определить истинность А: 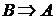. При формулировке теоремы слова «необходимо и достаточно» нередко заменяются словами: «тогда, и только тогда, когда» или «в том, и только в том, случае, если».

Продемонстрируем виды теорем на примере известной теореме Пифагора «В прямоугольном треугольни­ке квадрат гипотенузы равен сумме квадратов катетов». Выделим условие и заключение. Новая формулировка этой теоремы согласно наложенным требованиям, имеет вид: А 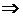В, т.е. «если дан прямо­угольный треугольник, то квадрат гипотенузы равен сумме квад­ратов его катетов». Первая часть формулировки: А – задан прямоугольный треугольник, представляет собой условие, вторая часть формулировки: В – квадрат гипотенузы равен сумме квад­ратов его катетов, является заключением, разъяснительная часть – это то, что идет речь о геометрической фигуре – треугольнике.

Для справедливости, высказывания, что «квадрат гипотенузы равен сумме квад­ратов его катетов» достаточно, чтобы треугольник был прямоугольным. Для справедливости, высказывания: «задан прямоугольный треугольник» необходимо, чтобы квадрат гипотенузы равен сумме квад­ратов его катетов.

Справедлива и обратная теорема: В 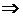А, а именно: «Если квадрат большей стороны треугольника равен сумме квад­ратов двух его других сторон, то треугольник является прямоугольным».

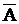
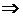
Справедлива и противоположная теорема: 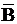, а именно: «Если треугольник не является прямоугольным, то квадрат большей стороны треугольника не равен сумме квад­ратов двух его других сторон ».

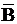
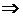
Справедлива и теорема, обратная противоположной теореме: 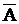, а именно: «Если квадрат большей стороны треугольника не равен сумме квадратов двух его других сторон, то треугольник не является прямоугольным».

Таким образом, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что справедлива следующая равносильность: , которая называется законом контрапозиции.