Функционально полные системы функций.

Запишем таблицу функций 1-й перем.:

x	y1	y2	y3	y4

y₁ – функция константы О ;

y₂ – переменная х ;

y₃ – отриц. переменная х ;

y₄ – конст-ты 1.

Для алгебры с двузначной логикой составим аналогичную таблицу всех возможных функций.

х1

х2

F0

F1

F2

F3

F4

F5

F6

F7

F8

F9

F10

F11

F12

F13

F14

F15

Некоторые из этих функций встречались ранее :

F₁(x₁, x₂) = x₁ * x₂ - дизъюнкция

F₆(x₁, x₂) = x₁ Å x₂ - слож. по модулю 2

F₇(x₁, x₂) = x₁ x₂ - конъюкция

Сведем в таблицу :

Функция	Название	Предназначение
F0	конст-та 0	Æ
F1	конъюкция	Логич. умнож. х1х2
F2	отрицание по х2	х1 2
F3	повт-ль х1	х1
F4	запрещение по х1	1х2
F5	повт-ль х2	х 2
F6	сумма по mod 2	х1Åх2
F7	дизъюнкция	логич. сложен. х1 х2
F8	стрелка Пирса	х1 ¯ х2
F9	эквив-ти	х1 ~х2
F10	отрицание х2	2
F11	импликация по х2	х2®x1
F12	отрицание х1	1
F13	импликация по х1	x1 ® х2
F14	отр. конъюкции	1 2
F15	конст-та 1

Функционально-полной системой алгебры Буля – набор функций Р_к, с помощью которых может быть выраженна любая функция из Р_к.

Тривиальной функционально-полной системой является весь набор функций из Р_к.

Базисом алгебры Буля называется функционально-полная система, которая перестает быть таковой при выбрасывании из неё любой функции.

Примером алгебры с функционально-полной системой, но не являющейся базисом является функция вида :

А = < M, , &, - >

На основании законов де Моргана из неё можно получить алгебры с базисами.

А₁ = < M, , - > , А₂ = < M, &, - >

Принцип нахождения функционально-полных систем и базисов для Р_к .

Будем искать такой набор из Р_к, с помощью которого можно представить функции дезъюнкции, конъюкции, отрицания, а следовательно и все остальные функции. Для изучения свойств пространства Р₂ , т. е. Функция от двух переменных, представим все функции с помощью операций дезъюнкции, конъюкции и отрицания.

F1 = х1*х2

F2 = х1* 2

F4 = 1*х2

F6 = х1Åх2 = 1*х2 х1* 2

F7 = х1 х2

F8 = 1* 2 = 1 2

F9 = 1 2 х1х2 = х1Åх2

F10 = 2

F11 = 1 2 х1 2 х1х2 = x1 2

F12 = 1

F₁₃ = _{1 2 1}х₂ х₁х₂ = ₁ х₂

F₁₄ = _{1 2 1}х₂ х_{1 2} = _{1 2} = _{1 2}

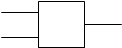
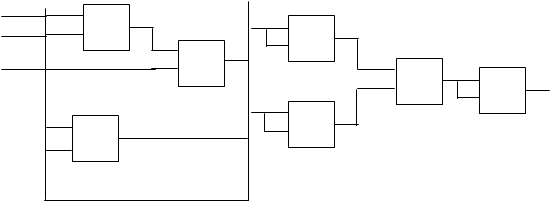
Для каждой из перечисленных функций существует двух ходовой логический элемент.

Изобразим эти элементы.

F₁ = x₁x₂ F₂ = x_{1 2} F₄ = ₁x₂

x₁ x₁ x₁

x₂ & y₁ x₂ & y₂ x₂ & y₄

F₆ = х₁Åх₂ F₇ = х₁ х₂ F₈ = _{1 2}

x₁ x₁ x₁

x₂ y₆ x₂ 1 y₇ x₂ 1 y₈

F₉ = х₁Åх₂ F₁₀ = ₂ F₁₁ = x_{1 2}

x₁ x₁ x₁

x₂ y₉ x₂ 1 y₁₀ x₂ 1 y₁₁

F₁₂ = ₁ F₁₃ = ₁ х₂ F₁₄ = _{1 2}

x₁ x₁ x₁

x₂ 1 y₁₂ x₂ 1 y₁₃ x₂ & y₁₄

На основании этих элементов можно синтезировать любую логическую функцию.

f(х₁,х₂,х₃) = х₁х₂х_{3 1}х₂ х_{1 2 1 2 3}

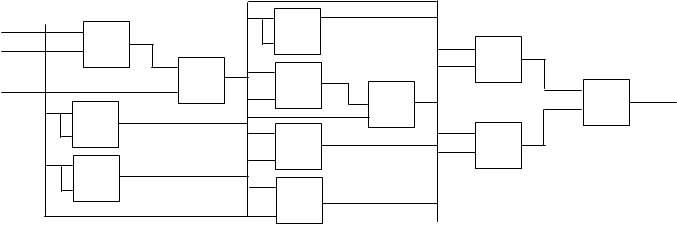_{02 07}

^{x1 00 1}

^{x2 01 &} ₀₃ ⁰⁴ ₁₂

₀₄ ⁰⁵ ₀₉ ¹

^{x3 02 &} ₀₆ ^& _{08 09 1 14 f}

⁰⁰ ₁ ^{07 &}

⁰⁵ ₁₀ ¹⁰

₀₁ ^{01 &} ₁₁ ¹

¹ ₀₀

_& ¹¹

₀₆

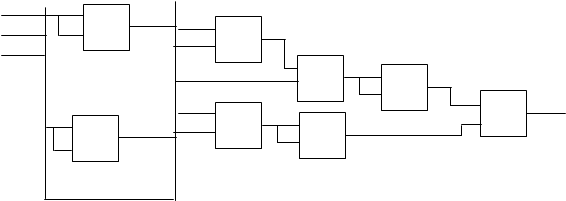
Реализуем функцию вида f(х₁,х₂,х₃):

f(х₁,х₂,х₃) = х_{1 2}х₃ & ₁х₃

^{x1 00} ₀₄

^{x2 01 &} _{03 04 1} ⁰⁶

_{x3 02 &} ⁰⁴

^& _{08 1} ^{f 09}

⁰⁵ ₀₇

_& ^{05 05 1}

f(х₁,х₂,х₃) = х_{1 2}х_{3 1}х₃ = ₁ х_{2 3} x_{1 3}

_{x1 00 00}

_{x2 01 00} ^{1 03 03} _{1 05}

_{x3 02} ⁰¹

_{04 1 06}

₀₈

₀₂ ^{00 1 10 f}

_{02 1} ^{04 04 1} _{07 1} ⁰⁹

СВОЙСТВА БУЛЕВЫХ ФУНКЦИЙ.

Функциональным классом называется множество всех функций, обладающих определенным свойством.

Функциональный класс замкнутый,если суперпозиция этого класса принадлежит этому же классу.

Например, класс функций, полученных с помощью дизъюнкции аргументов замкнут.

y(x₁,x₂) = x₁ x₂ ,где x₂(z₁,z₂) = z₁ z₂

y(x₁,x₂(z₁,z₂)) = y(x₁,z₁,z₂) = x₁ z₁ z₂

Перечислим некоторые свойства. Для булевой функции определим понятие набора.

Набор – фиксируемое значение аргументов функции d, t d = {0110}

Между различными наборами установим соотн. сравнения:

d₁ > d₂ , если любой элемент набора d₁ ³ соответственно элементу из набора d₂

d₁ = (11010)

d₂ = (01010) Þ d₁ > d₂

t₁ = (01001)

t₂ = (10100) Þ 2 набора несравнимы

d = (d₁, d₂, …,d_n)

t = (t₁, t₂, …,t_n) наборы знач. перем. знач. и считается d > t , если d_i > t_i

ТЕОРЕМА.

Если булева функция может быть представлена в нормальной дизъюктивной форме без отрицания, то эта функция монотонна.

ДОКАЗАТЕЛЬСТВО.

Возьмем произвольные значения d и t, причем d £ t. В этом случае условию теоремы удовлетворяют следующие возможности:

у( d ) = 0 , у ( t ) = 0

у( d ) = 0 , у ( t ) = 1

у( d ) = 1 , у ( t ) = 1

Откуда следует, что для доказательства теоремы достаточно доказать следующее утверждение:

если d £ t, то у ( d ) = 1 у ( t ) = 1

Докажем это утверждение.

Если у( d ) = 1, то всегда найдется интервал, для которого выполняется следующее условие:

x_j1, x_j2 … x_jk|_d = 1, где d_j1 = d_j2 = d_jk = 1

j - номер набора перем.без отрицания, тогда

t_j1 = t_j2 = t_jk = 1 Þ x_j1, x_j2 … x_jk|_t = 1

значит у( t ) = 1

Следствием теоремы является замкнутость класса монотонных функций.

Например:

y(х₁,х₂,х₃) = х₁х₂ х₁х₃ х₂х₃ , где х₂(z₁,z₂) = z₁ z₂

тогда: y(x₁,x₂(z₁,z₂)x₃) = x₁(z₁ z₂) x₁x₃ x₃(z₁ z₂) =

= x₁z₁ x₂z₂ x₁x₃ x₃z₁ x₃z₂

Так как результирующая функция не содержит отрицания, то она является монотонной.