Стандартные формы представлений формул

МНОЖЕСТВ.

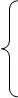На 1 определении М₁,М₂,М₃ совокупность М_i назовем порожд-ми множествами пространства и определим М_i по универсальной формуле:

М_i ; d_i =1;

M_i^di = d_i={0;1}

_i ; d_i =0;

Мi = i = {0,1}

Mi; i=0;

M_i, d_i – первичный термом

K_i = 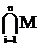_i^di - конституентой

n - число порожденных множеств.

Перечислим все конституенты нашего примера:

К₀ = _{1 2 3} К₁ = _{1 2}М₃ К₂ = ₁М_{2 3} К₃ = ₁М₂М₃

К₄ = М_{1 2 3} К₅ = М_{1 2}М₃ К₆ = М₁М_{2 3} К₃ = М₁М₂М₃

Очевидно, что каждой приведенной коституенте может быть сопоставлено двоичное трехразрядное число , причем каждый разряд будет равен d_i первичного терма:

К₀ = 000; К₁ = 001; К₂ = 010; К₄ =011; К₅ = 100; К₆ = 110; К₇ = 111.

Если учесть,что каждой конституенте длины П можно сопоставить n разр.

двоичное число, то общее количество конституент равно:

N = 2ⁿ

1) Выражения, заданные с помощью формул ,могут быть упрощены.

2) Необходимые шаги для упрощения не всегда очевидны и сложность упрощения находится в прямой зависимости от числа аргументов в формуле.

3) Для упрощения выражения произв. вида и произв. количества аргументов необходимо использовать математический аппарат минимизации функций подмножеств.

Пересечение двух различных конституент - пустое множество.

Пересечение двух конституент – есть пересечение всех первичных термов их составляющих, если конституенты не равны , то найдется хотя бы 1 разряд с несовпадающими первичными термами.

Обозначим этот разряд через i.

M_i^di *M_i^di*= Æ

Объединение всех коституент,порожденных множествами M_i на универсальном множестве равно самому универсальному множеству:

I= 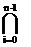(M_i È _i)

n=1 M₁, ₁ M₁+ ₁=I

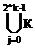n=k _j = I

С помощью конституент, образованных множествами M_i ,можно представить исходное универсальное множество.

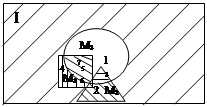
1. Проиллюстрируем на графическом примере:

(универсальное множество I, внутри М₁-квадрат, М₂-треугольник, М₃-круг).

В дополнение к рассматриваемым свойствам ,рассмотрим сколько множеств на I можно образовать из конституент.

Для этого произвольному множеству сопоставим m-разрядное двоичное число,где m-длина конституент. При этом 0-отсутствие конституенты, 1-присутствует.

Так например, двоичному числу

01101001 соответствует множество, из объединенных 0,3,5,и 6 конституент.

Вместо двоичных чисел можно использовать их десятичный эквивалент:

d = 1+2³+2⁵+2⁶ = 1+8+32+64 = 40+ 65 = 105

Если любому, образованному из конституент, множеству соответствует m-разрядное двоичное число, то таких множеств может быть 2^m,а так как число конституент = 2ⁿ , где n-число образованных множеств,то общее число, которое образуется из конституент = 2^{2^n}

Для иллюстрации это количество -256.

Рассмотрев понятие конституент зададимся вопросом:»Как конституенты связаны с функциями от образующих множеств?»

МАТЕМАТИЧЕСКИЕ УТВЕРЖДЕНИЯ.

Множество M_i равно объединению всех конституент ,содержащих M_i

Рассмотрим равенство:

I = 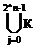_j-1

Возьмем пересечение левых и правых частей с M_i

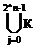Mi = _j-1M_i

Рассмотрим выражение К_j,M_i. Для него возможны два случая:

1.K_j не содержит в себе M_i, Ki*Mi = Æ

2.K_j Ì M_i , K_j*M_i =K_j

Следовательно, M_i можно представить в виде:

М_i = 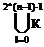_l

k_l -конституенты,содержащие M_i.

ТЕОРЕМА.

Любая функция от порождающих множеств представима в виде объединения конституент.

Из аксиоматичного построения следует,что все операции представимы через операции объединения и отрицания.

Следовательно, достаточно доказать ,что объединение порождающих множеств представимо через объединение конституент, а так же ,что отрицание объединения конституент ,так же представимо через объединение множеств.

Для доказательства рассмотрим объединение произвольно образованных множеств M_i и М_к.

Согласно утверждению (M_i È М_к) ,записывающихся в виде:

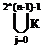М_i È М_к = _j+ 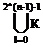_l М_i È М_к = 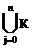_j

при этом М – различно,так как различно число совпадающих конституент в представлениях множеств M_i иМ_к.

Остается доказать,что дополнения к объединению конституент в свою очередь есть объединение конституент .

Так как универсальльное множество является объединением всех конституент, ясно ,что если взять объединение некоторых из них, то оставшиеся конституенты будут дополнительными к исходному объединению.

Рассмотрим пример:

Функция от множеств А,В,С

f(A,В,С) = А(В È ((С 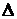А)\В)) = А(В È ((С È С )\В)) = А(В È (С È А) ) =

А(В È С È А ) = АВ È А = А È АВС È АВ

Из пересечения АВ получена АВС È С. Ясно ,чтобы получит трех-разрядную конституенту, необходимо до термов АВ добавить С, а так как произв-но множество М:

М(С È ) = МС È М АВ = АВС È АВ

то просто получим из АВ трехразрядную конституенту.

Итак , любая функция от порождающих множеств , может быть представлена в виде объединения коституент и оно называется совершенной норм.Кантора (СНФК).

Если в представлении функции участвовали конституенты меньшей длины, то оно называется норм. формой Кантора (НФК).

Для получения РФК нужно минимизании СНФК любым (аналитическим, графическим,графо-аналитическим способом).

Назовем интервалами универсального пространства ранга n все коституенты длина l =1, n

Если какая-либо С₁ (интерв.) = С₂È С₃, то говорят что С₁ включает в себя С₂ и С₃ или С₁ покрывает С₂ и С₃

Из этого следует , что функция ,представленная в СНФК равна:

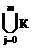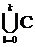f (A,В,С) = _j= _l

где C_l - интервалы,покрывающие все конституенты К_j .

Если рассмотреть предыдущий пример,то можно заметить ,что f(А,В,С):

f (A,В,С) = АВ È А

где, АВ покрывает АВС и АВ , а втор. совпадает с А .