Возьмем правую часть равенства. Согласно закону ассоциативности
раскроем скобки и получим:
(АÈС)Ç(ВÈС)=АÇВÈСÇВÈАÇСÈСÇС=АÇВÈС (упростили используя
закон поглощения ). Из записи закона ассоциативности и закона
дистрибутивности видно, что один закон можно получить из другого,
заменив знаки “È” и “Ç”, следовательно, законы двойственны.
4. Закон поглощения
Если А содержится в В, то АÈB=В.
Согласно аксиоме объединения в результирующее множество входят элементы, принадлежащие хотябы одному А или В, а так как все А входят в В то справедливо:
АÈB=В
АÈАÇМ=А
Исходя из определения операции пересечения ясно, что АÇМ содержится в А.В итоге получаем А.
Следствие:
Если М=1, то АÈА=А
5. Свойство степени.
Если множество пересекается с самим собой, то из определения пересечения следует
АÇА=А
6. Законы де Моргана.
Эти законы позволяют выразить законы объединения и пересечения друг через друга с использованием операции дополнения :
 а) АÈВ=
а) АÈВ=  Ç
Ç 

Доказательство :
Обозначим через М: М=АÈВ и  =
=  Ç
Ç  . Если теперь объединение М и
. Если теперь объединение М и  даст единичное множество, то закон будет доказан.
даст единичное множество, то закон будет доказан.
М È  = А È В È
= А È В È  Ç
Ç  = АÈ(В È
= АÈ(В È  )Ç(В È
)Ç(В È  ). Используя определение дополнения получим :
). Используя определение дополнения получим :
М È  = АÈВÈ
= АÈВÈ  =1ÈВ=1=I
=1ÈВ=1=I
 б) АÇВ=
б) АÇВ=  È
È 

Доказательство :
Обозначим через М: М=АÇВ и  =
=  È
È  . Если теперь объединение М и
. Если теперь объединение М и  даст единичное множество, то закон будет доказан.
даст единичное множество, то закон будет доказан.
М È  = А Ç В È
= А Ç В È  Ç
Ç  =(
=(  È А) Ç (В È
È А) Ç (В È  )È
)È  = ВÈ
= ВÈ  È
È  =1È
=1È  =1=I
=1=I
Законы де Моргана так же являются двойственными.
АÇВ=АВ.
ВЫВОДЫ ПО РАЗДЕЛУ.
1. АÌА
2. Если АÌВ и ВÌА, то А=В
3. Если АÌВ и ВÌС, то АÌС
4. Æ Ì A
5. А Ì I
6. А È В =В È А
7. А Ç В =В Ç А
8. АÈ(ВÈС)=(АÈВ)ÈС
9. АÇ(ВÇС)=(АÇВ)ÇС
10. А È А = А
11. А Ç(ВÈС)=(АÇВ)È(АÇС)
12. А È (ВÇС)=(АÈВ) Ç (АÈС)
13. А È Æ = А
14. А È I= I
15. А Ç I = A
16. А Ç A = A
17. А Ç Æ = Æ
18. Если АÌВ, то АÈВ=В, АÇВ=А
19. А È  = I
= I
20. A Ç  = Æ
= Æ
21. 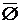 =I
=I
22. 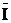 =Æ
=Æ
23.  = A
= A
24. Если АÌВ, то  Ì
Ì 
25. ( 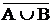 ) =
) =  Ç
Ç 
26. ( 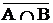 ) =
) =  È
È 
МИНИМИЗАЦИЯ ФУНКЦИОНАЛЬНОГО ПРЕДСТАВЛЕНИЯ
МНОЖЕСТВ.
Определим функцию от фрагментов, являющихся множествами. Функцией будем называть взаимооднозначное отображение элементов группы множеств Аi в элементы множества С. Если каждому элементу С соответствует некоторый элемент Аi, такую функцию называют всюду значимой
С = f (Ai)
f – функция переводит элементы Ai во множество С.
Если пересечение множеств обозначать как функциональную операцию Р , то
Р (А,В) = АВ
На единичном множестве 1 заданы множества А,В,С. В этом случае с помощью известной операции над множествами переводим исходное множество в какое-либо другое.
f (А,В,С) = АВС È А  С È
С È  В
В  È
È 

 È АВ È AС È
È АВ È AС È  С È
С È  В;
В;
Записанное выражение назовем формулой. Определим сложность формулы, как количество, содержащихся в ней исходных множеств. Для приведенного примера сложность =20. При аналазе формул первым вопросом является: «Можно ли уменьшить сложность формулы?» Сделаем это на примере применяя законы дистрибутивности и поглощения
f(А,В,С) = АВС È А 
 È
È  В
В  È
È 

 È А(В È С) È
È А(В È С) È  (В È С) =
(В È С) =
= АВС È А 
 È
È  B
B  È
È 

 È В È С = ВÈ А
È В È С = ВÈ А 
 È
È 

 È С =
È С =
= 
 È В È С =
È В È С = 
 È
È 
 =1
=1
f(А,В,С) = АС È  С È
С È  ВС È АВС È АВ
ВС È АВС È АВ  È
È  В
В  = АС È
= АС È  С È
С È  В È АВ =
В È АВ =
=В È АС È  С;
С;
Или :
F(А,В,С) = АС È  С È
С È  ВС È АВС È АВ
ВС È АВС È АВ  È
È  В
В  = АС È
= АС È  С È ВС È АВ
С È ВС È АВ  È È
È È  В
В  = АС È
= АС È  С È ВС È В
С È ВС È В  = С È В
= С È В 
Как видно из примеров минимизация одних и тех же функций может дать разные результаты при применении одних и тех же законов.
