Тема 5. « Составление различных уравнений параболы».
Определение 1. Парабола-это линия, состоящая из множества точек плоскости, равноудалённых от одной точки ( фокуса) и данной прямой (директрисы), которая не проходит через фокус ( F) Определение 2. Расстояние от фокуса до директрисы называется параметром параболы (p). Существует IV вида параболы: Симметрично оси Х ( I)    - уравнение параболы - уравнение параболы  - уравнение директрисы, F( - уравнение директрисы, F(  ; 0) – координаты фокуса ; 0) – координаты фокуса  - уравнение со смещённой вершиной О(a; b) Симметрично оси Х (II): - уравнение со смещённой вершиной О(a; b) Симметрично оси Х (II):   - уравнение директрисы, F(- - уравнение директрисы, F(-  ; 0) – координаты фокуса ; 0) – координаты фокуса   - уравнение параболы - уравнение параболы  - Уравнение со смещённой вершиной О(a; b) ___________________________________________________________________ Симметрично оси Y (III): - Уравнение со смещённой вершиной О(a; b) ___________________________________________________________________ Симметрично оси Y (III):    - уравнение параболы - уравнение параболы  уравнение директрисы, F ( 0; уравнение директрисы, F ( 0;  )- координаты фокуса )- координаты фокуса  - Уравнение со смещённой вершиной О(a; b) ______________________________________________________________________ Симметрично оси Y (IV): - Уравнение со смещённой вершиной О(a; b) ______________________________________________________________________ Симметрично оси Y (IV):    - уравнение параболы - уравнение параболы  уравнение директрисы, F ( 0; - уравнение директрисы, F ( 0; -  )- координаты фокуса )- координаты фокуса  - Уравнение со смещённой вершиной О(a; b) Пример 1. Парабола проходит через точку А ( - 4; 10) симметрично оси ординат с вершиной в начале координат. Найдите уравнение директрисы и координаты фокуса. Решение: Парабола симметрична оси У и проходит через точку А ( - 4; 10), значит парабола III вида и имеет уравнение - Уравнение со смещённой вершиной О(a; b) Пример 1. Парабола проходит через точку А ( - 4; 10) симметрично оси ординат с вершиной в начале координат. Найдите уравнение директрисы и координаты фокуса. Решение: Парабола симметрична оси У и проходит через точку А ( - 4; 10), значит парабола III вида и имеет уравнение  . · Найдём p, для этого подставим координаты точки А, получим: . · Найдём p, для этого подставим координаты точки А, получим:  , 16 = 20р , 16 = 20р  . Уравнение параболы имеет вид: . Уравнение параболы имеет вид:  · Уравнение директрисы имеет вид: · Уравнение директрисы имеет вид:  . Подставим . Подставим  , получим: , получим:   - уравнение директрисы. · Фокус имеет координаты - уравнение директрисы. · Фокус имеет координаты  . Ответ: . Ответ:  , ,  . . |
Образец решения РТ « Аналитическая геометрия».
1. Парабола проходит через точку А ( - 4; 10) симметрично оси ординат с вершиной в начале координат. Найдите уравнение директрисы и координаты фокуса.
Решение: Парабола симметрична оси У и проходит через точку А ( - 4; 10), значит парабола III вида и имеет уравнение  .
.
· Найдём p, для этого подставим координаты точки А, получим:  ,
,
16 = 20р  . Уравнение параболы имеет вид:
. Уравнение параболы имеет вид: 
- Уравнение директрисы имеет вид:
 . Подставим
. Подставим  , получим:
, получим:

 - уравнение директрисы.
- уравнение директрисы.
- Фокус имеет координаты
 . Ответ:
. Ответ:  ,
,  .
.
2. Дано уравнение окружности  . Определите координаты центра и радиус этой окружности.
. Определите координаты центра и радиус этой окружности.
Решение:  ,
, 
 О ( 3; -5) – центр окружности, R =
О ( 3; -5) – центр окружности, R = 
Ответ: О ( 3; -5), R = 4.
3. Составьте уравнение гиперболы, если расстояние между фокусами 20, 
 .
.
Решение:  .
.  .
.
Подставим в формулу  значения а и с, получим:
значения а и с, получим: 
 .
.
Уравнение гиперболы имеет вид :  . Подставим значения а и b, получим:
. Подставим значения а и b, получим:  . Ответ:
. Ответ:  .
.
4. Составьте уравнение эллипса, проходящего через точки: А  и В
и В  .
.
Решение: Уравнение эллипса имеет вид:  . Подставим координаты точек, получим:
. Подставим координаты точек, получим:  Подставим значение
Подставим значение  в первое уравнение, получим:
в первое уравнение, получим:  ,
,
 . Подставим
. Подставим  и
и  в общее уравнение эллипса, получим
в общее уравнение эллипса, получим
Ответ:  .
.
5. Дано уравнение гиперболы  . Найдите полуоси и эксцентриситет.
. Найдите полуоси и эксцентриситет.
Решение: Приведём уравнение гиперболы к каноническому виду, т. е.

Эксцентриситет находим по формуле:  , получим:
, получим: 
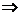
 . Ответ: а = 3, b =
. Ответ: а = 3, b =  .
.
ПРИМЕРНЫЕ КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1.Определите род точек разрыва функции
2. Исследуйте функцию  ( определите асимптоты, промежутки монотонности, точки экстремума, промежутки выпуклости). По результатам исследования постройте график функции.
( определите асимптоты, промежутки монотонности, точки экстремума, промежутки выпуклости). По результатам исследования постройте график функции.
3. Найдите площадь фигуры, ограниченной линиями  , у = 0.
, у = 0.
4.Найдите частное решение уравнения:,  , если у(1) = 5.
, если у(1) = 5.
5. Решите систему уравнений (любым методом) 
6. Составьте каноническое уравнение эллипса, проходящего через точки
А(  ; 0) и В( 4;
; 0) и В( 4;  ).
).
7 .Решите уравнение:  . Найдите : а)
. Найдите : а)  б)
б) 
8-13.Теоретические вопросы.
Теоретические вопросы к экзамену
1.Для раскрытия неопределённости  при вычислении пределов надо:
при вычислении пределов надо:
А) числитель и знаменатель разделить на высшую степень.
Б) числитель и знаменатель разложить на множители
В) применить второй замечательный предел
Г) числитель и знаменатель умножить на высшую степень.
2.Для раскрытия неопределённости  при вычислении пределов надо:
при вычислении пределов надо:
А) числитель и знаменатель разделить на высшую степень х.
Б) числитель и знаменатель разложить на множители
В) применить второй замечательный предел
Г) применить первый замечательный предел
3.Первый замечательный предел имеет вид :
a ) 
 б)
б)  в)
в) 
4.Закончите правило дифференцирования: 
5.Если функция убывает на некотором промежутке, то производная ….. на этом промежутке.
6.Если при переходе через точку х0 первая производная меняет знак
с «-» на «+», то х0 является точкой….
7.Операция по нахождению первообразной называется…
8.Запишите формулу Ньютона-Лейбница
9.Формула интегрирования по частям имеет вид:
а)  б)
б)  в)
в)  г)
г) 
10.Матрица, у которой элементы на главной диагонали равны 1, а все остальные равны 0, называется…
11.Сложение матриц выполнимо, если…
12.Метод решения систем уравнений, который основан на последовательном исключении неизвестных, называется…
13.Запишите каноническое уравнение гиперболы
14. Запишитеканоническое уравнение эллипса
15.Запишите уравнение прямой с угловым коэффициентом .
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ РАБОТ И ПОДГОТОВКИ К ЭКЗАМЕНУ
Основная литература:1) Григорьев В.П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования/
В.П. Григорьев, Ю.А. Дубинский.- 7-е изд., стер. - М. : Издательский центр « Академия», 2012.
2) Григорьев В.П. Сборник задач по высшей математике: учеб. пособие для студ. учреждений сред. проф. образования/
В.П. Григорьев, Т.Н. Сабурова. .- М. : Издательский центр « Академия», 2010.
Дополнительная литература: 1)Ю. М. Колягин . Математика : учебник СПО в 2 книгах / Ю. М. Колягин , Г.Л. Луканин , Г.Н. Яковлев – М. : Оникс, 2008
2)М.Я.Выгодский. Справочник по высшей математике/ М. Я. Выгодский. – М.: ООО « Издательство Астрель»: « Издательство АСТ», 2004
Интернет-ресурсы
ПРИЛОЖЕНИЕ 1

 , рад , рад |  0 0 |  |  |   |  |  |  |  |
 , град , град | 00 | 300 | 450 | 600 | 900 | 1800 | 2700 | 3600 |
 | 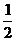 |  |  | -1 | ||||
 |  |  | 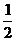 | -1 | ||||
 |  |  | - | - | ||||
 | - |  |  | - | - |
ПРИЛОЖЕНИЕ 2
Таблица производных.
| Функция (у =…) | Производная (  ) ) | Функция (у =…) | Производная (  ) ) | ||
| С ( постоянная) |  |  | |||
 ( (  ) ) |  |  |  | ||
 |  |  |  | ||
3)  |  |  |  | ||
| х |  |  | |||
 |  |  |  | ||
 | -  |  |  | ||
 |  |  |  | ||
 |  |
ПРИЛОЖЕНИЕ 3.
Таблица интегралов.
 , ,  |  |  | |||
 |  |  | |||
 |  |  | |||
 |  |  | |||
 +С +С |  |  | |||
 |  |  | |||
 |  |  | |||
 |
