Тема 4. «Решение систем линейных уравнений методом Гаусса».
Определение 1. Система линейных уравнений (СЛУ)–это система, содержащая m уравнений с n неизвестными. 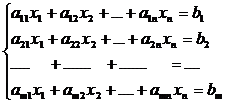 Систему можно записать в матричной форме: Систему можно записать в матричной форме: 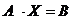 , где , где  , , 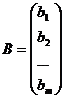  Определение 2.Матрица называется расширенной, если она дополнена столбцом свободных элементов. Обозначается Определение 2.Матрица называется расширенной, если она дополнена столбцом свободных элементов. Обозначается 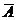 . . 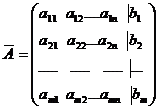 Определение 3: Совокупность чисел называется решением системы, если она обращает все уравнения в тождества. Определение 4: Система совместна, если имеет хотя бы одно решение, и несовместна если не имеет ни одного решения. Определение 5: Система неопределённая , если решений больше одного(бесконечно много). Определение 6: Система уравнений называется однородной, если все свободные члены равны нулю. ( Однородная система всегда совместна) Определение 7: Две системы называются эквивалентными(равносильными), если они имеют одно и то же решение. Эквивалентные системы получаются при элементарных преобразованиях матрицы над строками. ______________________________________________________________________ Решение систем методом Гаусса основано на последовательном исключении неизвестных. Алгоритмрешения систем методом Гаусса: 1) Записать расширенную матрицу системы линейных уравнений 2) Привести матрицу к ступенчатому виду с помощью элементарных преобразований над строками. 3) А)СЛУ определённая и совместная (имеет одно решение), если матрица принимает треугольный вид (решение находят подстановкой) Б) СЛУ неопределённая и совместная (имеет бесконечно много решений), если матрица принимает трапецеидальный вид. В) Определение 3: Совокупность чисел называется решением системы, если она обращает все уравнения в тождества. Определение 4: Система совместна, если имеет хотя бы одно решение, и несовместна если не имеет ни одного решения. Определение 5: Система неопределённая , если решений больше одного(бесконечно много). Определение 6: Система уравнений называется однородной, если все свободные члены равны нулю. ( Однородная система всегда совместна) Определение 7: Две системы называются эквивалентными(равносильными), если они имеют одно и то же решение. Эквивалентные системы получаются при элементарных преобразованиях матрицы над строками. ______________________________________________________________________ Решение систем методом Гаусса основано на последовательном исключении неизвестных. Алгоритмрешения систем методом Гаусса: 1) Записать расширенную матрицу системы линейных уравнений 2) Привести матрицу к ступенчатому виду с помощью элементарных преобразований над строками. 3) А)СЛУ определённая и совместная (имеет одно решение), если матрица принимает треугольный вид (решение находят подстановкой) Б) СЛУ неопределённая и совместная (имеет бесконечно много решений), если матрица принимает трапецеидальный вид. В) 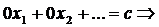 решения нет ( система не совместна) 4). Найти неизвестные. Пример 1. Решить систему линейных уравнений методом Гаусса: решения нет ( система не совместна) 4). Найти неизвестные. Пример 1. Решить систему линейных уравнений методом Гаусса: 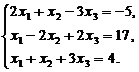 Решение. Расширенная матрица системы имеет вид Решение. Расширенная матрица системы имеет вид 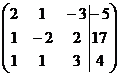 Шаг 1. Для удобства вычислений поменяем местами первую и вторую строки: Шаг 1. Для удобства вычислений поменяем местами первую и вторую строки: 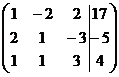 . Так как . Так как 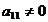 , то умножаем первую строку на (-2) и складываем со второй, умножаем первую строку на (-1) и прибавляем к третьей строке, тем самым исключим переменную , то умножаем первую строку на (-2) и складываем со второй, умножаем первую строку на (-1) и прибавляем к третьей строке, тем самым исключим переменную 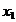 из всех строк, начиная со второй: из всех строк, начиная со второй: 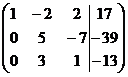 Шаг 2. Так как Шаг 2. Так как 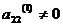 , то умножим вторую строку на (-3/5) и прибавим к третьей, таким образом исключим переменную , то умножим вторую строку на (-3/5) и прибавим к третьей, таким образом исключим переменную 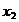 из третьей строки: из третьей строки: 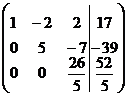 . Получили систему уравнений, соответствующую последней матрице: . Получили систему уравнений, соответствующую последней матрице: 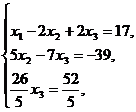 откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения 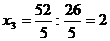 ; из второго уравнения найдем: ; из второго уравнения найдем: 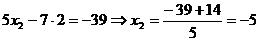 из первого уравнения : из первого уравнения : 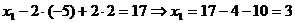 . Ответ: (3; -5; 2). Пример 2. Решить систему линейных уравнений методом Гаусса: . Ответ: (3; -5; 2). Пример 2. Решить систему линейных уравнений методом Гаусса: 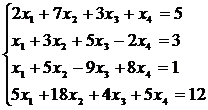 Решение: Расширенная матрица имеет вид: Решение: Расширенная матрица имеет вид: 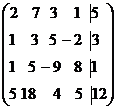 . Поменяем 1 и 2 строки . Поменяем 1 и 2 строки 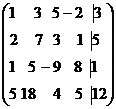 . Далее: 1стр . (-2)+2стр, 1стр . (-1) + 3 стр, 1 стр . (-5) + 4 стр. Получим: . Далее: 1стр . (-2)+2стр, 1стр . (-1) + 3 стр, 1 стр . (-5) + 4 стр. Получим: 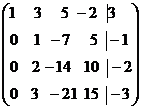 . Разделим вторую строку на 2, третью на 3, получим: . Разделим вторую строку на 2, третью на 3, получим: 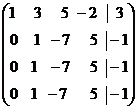 . Вычеркнем 3 и 4 одинаковые строки, останется . Вычеркнем 3 и 4 одинаковые строки, останется 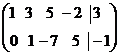 . Запишем в виде системы: . Запишем в виде системы: 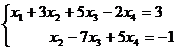 . Выразим из первого уравнения . Выразим из первого уравнения 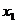 , а из второго уравнения , а из второго уравнения 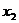 , получим: , получим: 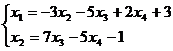 Подставим Подставим 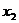 в первое уравнение, получим: в первое уравнение, получим: 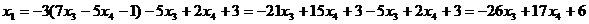 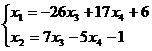 - общее решение системы, где - общее решение системы, где 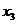 и и 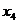 любые числа. Пусть любые числа. Пусть 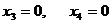 , тогда , тогда 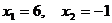 , значит (6; -1; 0; 0) – частное решение Ответ: , значит (6; -1; 0; 0) – частное решение Ответ: 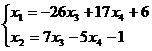 - общее решение, (6; -1; 0; 0)- частное решение - общее решение, (6; -1; 0; 0)- частное решение |
Наши рекомендации
Число: 2085
