Тема 2. « Применение производной к исследованию функций»
 Пусть Пусть 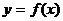 - дифференцируемая на интервале - дифференцируемая на интервале  функция. Определение 1. Функция функция. Определение 1. Функция 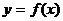 возрастает на возрастает на  тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка. Определение 2. Функция тогда и только тогда, когда её производная больше или равна нулю в любой точке этого промежутка. Определение 2. Функция 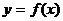 убывает на убывает на 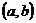 тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка. тогда и только тогда, когда её производная меньше или равна нулю в любой точке этого промежутка.
Определение 3. Критическими точками функции (первого рода) называются точки, в которых производная функции равна нулю или не существует. Определение 4. Пусть функция 1. если производная 2. если производная
Для нахождения промежутков монотонности и точек экстремума функции используется следующий алгоритм: 1. Найдите область определения функции. 2. Найдите первую производную функции. 3. Определите критические точки первого рода (f'(xo)=0 или f'(xo) не существует). 4.На числовой оси отметьте критические точки и определите знаки производной на каждом из получившихся интервалов. (подставить удобное число в производную и вычислить). 5.Выпишите интервалы монотонности. Выпишите точки экстремума функции (если они есть), используя соответствующие критерии, вычислите значения функции в точках экстремума. Пример 1. Найдите промежутки монотонности и точки экстремума функции Решение. 1. Данная функция определена на множестве R. 2. Найдем первую производную функции: 3. Определим критические точки первого рода (у'=0): х1=1 или х2=5. 4. На числовой оси отметим критические точки х1=1 и х2=5. Эти точки разбивают область определения функции на три интервала (-∞;1), (1;5); (5;+∞). Расставим знаки производной функции у' = при х=0 при х=2 при х=6
5. Согласно критерию возрастания и убывания функция Согласно критерию нахождения точек экстремума х=1 – точка максимума, х=5 – точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
Ответ: Определение 5. График функции Определение 6. График функции Определение 7. Точка графика непрерывной функции, в которой меняется характер выпуклости, называется точкой перегиба.
Так, график функции на рис.1. является выпуклым на промежутках (- Критерий выпуклости-вогнутости функции: если функция если функция
Таким образом, исследовать функцию на выпуклость-вогнутость означает найти те интервалы области определения, в которых вторая производная сохраняет свой знак. Определение 8. Критическими точками функции второго рода называются те точки, в которых вторая производная равна нулю или не существует. Только критические точки могут быть точками перегиба. Для их нахождения используется следующая теорема: Теорема (достаточное условие существования точек перегиба). Если вторая производная При исследовании функции 1. Найдите область определения функции. 2. Найдите первую производную функции 3. Найдите вторую производную функции 4. Определите критические точки второго рода ( 5. На числовой оси отметьте критические точки второго рода и определите знаки второй производной на каждом из получившихся интервалов.( подставить удобное число во вторую производную и вычислить) 6. Найдите интервалы выпуклости-вогнутости графика функции, используя соответствующие критерии; выпишите абсциссы точек перегиба (если они есть) и найдите значение функции в этих точках. Пример 2. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции Решение. 1. Данная функция определена на множестве R. 2. Найдем первую производную функции: 3. Найдем вторую производную функции: 4. Определим критические точки второго рода ( 5. На числовой оси отметим критическую точку х=3. Она разбивает область определения функции на два интервала (-∞;3) и (3;+∞). Расставим знаки второй производной функции при х=0 при х=4
 6. Согласно критерию выпуклости-вогнутости график функции Значение х=3 – абсцисса точки перегиба. Вычислим значение функции при х=3:
Ответ: график функции вогнутый при х Пример 3. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции Решение. 1. Данная функция определена в том случае, когда знаменатель отличен от нуля: х-7≠0 2. Найдем первую производную функции:
= 3. Найдем вторую производную функции: = = Вынесем в числителе 2∙(х-7) за скобки:
= 4. Определим критические точки второго рода:
5. На числовой оси отметим критическую точку х=7 выколотой точкой, поскольку в этой точке функция при х=6 при х=8
 6. Согласно критерию выпуклости-вогнутости график функции Точка с абсциссой х=7 не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв). Ответ: график функции вогнутый при х |

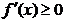
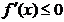
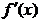 при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
при переходе через точку хо меняет знак с плюса на минус, то точка хо является точкой максимума;
 хо
хо 
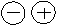
 хо
хо 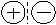
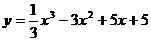 .
.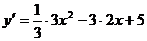 =
= 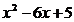 .
.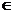 (-∞;1) у'(0)=5>0;
(-∞;1) у'(0)=5>0;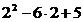 =-3<0;
=-3<0;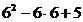 =5>0.
=5>0.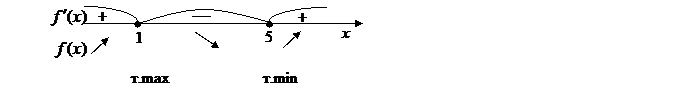
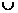 [5;+∞), убывает при х
[5;+∞), убывает при х  =
= 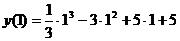 =
= 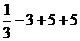 =
= 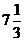 - максимум функции;
- максимум функции;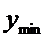 =
= 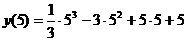 =
= 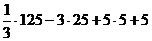 =
= 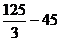 =
= 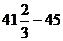 =
= 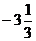 - минимум функции.
- минимум функции.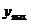 =
= 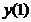 =
=  =
= 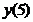 =
= 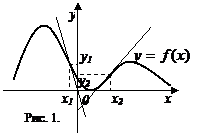 Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.
Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.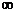 ;х1) и (х2; +
;х1) и (х2; + 
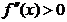

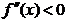
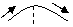
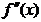 при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба.
при переходе через точку хо меняет знак, то точка графика с абсциссой хо является точкой перегиба. 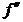 (xo)=0 или
(xo)=0 или 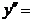
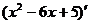 =2х-6.
=2х-6.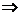 х=3.
х=3.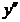 (0)=-6<0;
(0)=-6<0;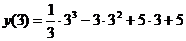 =
= 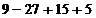 =2. Итак, точка с координатами (3;2) – точка перегиба.
=2. Итак, точка с координатами (3;2) – точка перегиба.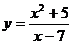 .
.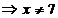 .
.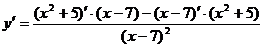 =
= 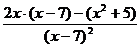 =
= 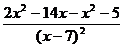 =
=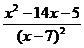 .
.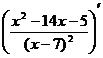 =
=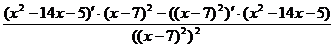 =
=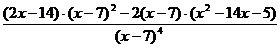 .
.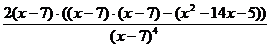 =2∙
=2∙ 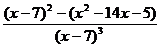 =
=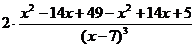 =
= 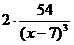 =
= 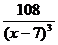 .
.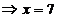 - критическая точка второго рода.
- критическая точка второго рода.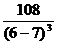 <0;
<0;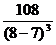 >0.
>0.