Раздел 1. « комплексные числа»

РАЗДЕЛ 1. « КОМПЛЕКСНЫЕ ЧИСЛА»

Тема 1. «Действия над комплексными числами»

- алгебраическая форма записи комплексного числа, где а –действительная часть комплексного числа, b – мнимая часть комплексного числа, i – мнимая единица, . Действия над комплексными числами в алгебраической форме , -данные комплексные числа 1.Сложение: Чтобы найти сумму двух комплексных чисел , надо по отдельности сложить действительные и мнимые части, т.е. Пример 1: , , 2. Вычитание: Чтобы найти разность двух комплексных чисел , надо по отдельности вычесть действительные и мнимые части, т.е. Пример 2: , , 3.Умножение: Произведение комплексных чисел находится по распределительному закону умножения и определению мнимой единицы, т.е.раскрыть скобки, привести подобные, учитывая, что Пример 3: , , 4. Деление:Числитель и знаменатель дроби умножить на выражение, сопряжённое знаменателю Для комплексного числа , сопряженным является число . Для комплексного числа , сопряженным является число . Пример 4: ,

Тема 2. « Нахождение модуля и аргумента комплексных чисел».

Каждое комплексное число a + bi геометрически изображается на плоскости как точка М(а;b) или как вектор ОМ. Ось Х является действительной осью, Ось Y является мнимой осью. Пример 1: Комплексное число Положение на плоскости Координаты точки Начало координат (0 ; 0) Ось Х (-3; 0) Ось Х (2; 0) Ось Y (0; 1) Ось Y I четверть (2; 3) II четверть (- 4; 1) III четверть (-3; -3) IV четверть Модулем ( r) комплексного числа называется длина вектора, соответствующего этому числу Пример 2: , , Аргументом ( ) комплексного числа называется величина угла в радианах между положительным направлением действительной оси и вектором комплексного числа. Аргумент обозначается как ϕ = arg(z) и принадлежит полуинтервалу [0, 2 ). , если поворот против часовой стрелки, , если поворот по часовой стрелки. Аргумент комплексного числа можно найти через вспомогательный угол , . (Приложение 1) Координаты точки Четверть Аргумент комп. числа (+; +) первая (-; +) вторая (-; -) третья (+; -) четвёртая Пример 3: Найдём аргумент комплексного числа . -координаты точки на плоскости данного числа, IV четверти. , так как число находится в IV четверти, то . Ответ: - тригонометрическая форма записи комплексного числа, где r – модуль комплексного числа, - аргумент комплексного числа Пример 4: Найти тригонометрическую форму записи комплексного числа . 1) Найдём модуль: . 2) Найдём аргумент: (-1;1) – координаты точки данного числа, II четверти. . Так как число находится во II четверти, то 3) - тригонометрическая форма комплексного числа

РАЗДЕЛ 3. «Применение дифференциального исчисления»

РАЗДЕЛ 5. « Решение дифференциальных уравнений».

ПРИМЕРНЫЕ КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ДИСЦИПЛИНЕ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ

1.Определите род точек разрыва функции

2. Исследуйте функцию ( определите асимптоты, промежутки монотонности, точки экстремума, промежутки выпуклости). По результатам исследования постройте график функции.

3. Найдите площадь фигуры, ограниченной линиями , у = 0.

4.Найдите частное решение уравнения:, , если у(1) = 5.

5. Решите систему уравнений (любым методом)

6. Составьте каноническое уравнение эллипса, проходящего через точки

А( ; 0) и В( 4; ).

7 .Решите уравнение: . Найдите : а) б)

8-13.Теоретические вопросы.

Теоретические вопросы к экзамену

1.Для раскрытия неопределённости при вычислении пределов надо:

А) числитель и знаменатель разделить на высшую степень.

Б) числитель и знаменатель разложить на множители

В) применить второй замечательный предел

Г) числитель и знаменатель умножить на высшую степень.

2.Для раскрытия неопределённости при вычислении пределов надо:

А) числитель и знаменатель разделить на высшую степень х.

Б) числитель и знаменатель разложить на множители

В) применить второй замечательный предел

Г) применить первый замечательный предел

3.Первый замечательный предел имеет вид :

a ) б) в)

4.Закончите правило дифференцирования:

5.Если функция убывает на некотором промежутке, то производная ….. на этом промежутке.

6.Если при переходе через точку х₀ первая производная меняет знак

с «-» на «+», то х₀ является точкой….

7.Операция по нахождению первообразной называется…

8.Запишите формулу Ньютона-Лейбница

9.Формула интегрирования по частям имеет вид:

а) б) в) г)

10.Матрица, у которой элементы на главной диагонали равны 1, а все остальные равны 0, называется…

11.Сложение матриц выполнимо, если…

12.Метод решения систем уравнений, который основан на последовательном исключении неизвестных, называется…

13.Запишите каноническое уравнение гиперболы

14. Запишитеканоническое уравнение эллипса

15.Запишите уравнение прямой с угловым коэффициентом .

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ РАБОТ И ПОДГОТОВКИ К ЭКЗАМЕНУ

Основная литература:1) Григорьев В.П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования/

В.П. Григорьев, Ю.А. Дубинский.- 7-е изд., стер. - М. : Издательский центр « Академия», 2012.

2) Григорьев В.П. Сборник задач по высшей математике: учеб. пособие для студ. учреждений сред. проф. образования/

В.П. Григорьев, Т.Н. Сабурова. .- М. : Издательский центр « Академия», 2010.

Дополнительная литература: 1)Ю. М. Колягин . Математика : учебник СПО в 2 книгах / Ю. М. Колягин , Г.Л. Луканин , Г.Н. Яковлев – М. : Оникс, 2008

2)М.Я.Выгодский. Справочник по высшей математике/ М. Я. Выгодский. – М.: ООО « Издательство Астрель»: « Издательство АСТ», 2004

Интернет-ресурсы

ПРИЛОЖЕНИЕ 1

, рад	0
, град	00	300	450	600	900	1800	2700	3600
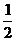							-1
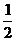						-1
					-		-
	-					-		-

ПРИЛОЖЕНИЕ 2

Таблица производных.

	Функция (у =…)	Производная ( )		Функция (у =…)	Производная ( )
	С ( постоянная)
	( )
	3)
	х
		-

ПРИЛОЖЕНИЕ 3.

Таблица интегралов.

	,
	+С

РАЗДЕЛ 1. « КОМПЛЕКСНЫЕ ЧИСЛА»