Химическое равновесие. Закон действующих масс

В.А. Зазимко

Теоретические основы

расчета до- и сверхзвуковых

струйных течений

с учетом физико-химических

превращений

Министерство образования и науки Российской Федерации

Балтийский государственный технический университет «Военмех»

В.А. Зазимко

Теоретические основы

расчета до- и сверхзвуковых

струйных течений

с учетом физико-химических

превращений

Санкт-Петербург

УДК 532.517(075.8)

З 16

З 16

УДК 532.517(075.8)

Утверждено

редакционно-издательским

советом университета

Р е ц е н з е н т ы: д-р физ.-мат. наук проф. каф. «Аэродинамика
и динамика полета» Акад. гражд. авиации С.А.Исаев; д-р техн. наук, проф., зав. каф. М4 БГТУ В.Н.Усков

ISBN 5-85546- 216-1© В.А. Зазимко, 2006

© БГТУ, 2006

П Р Е Д И С Л О В И Е

Важность изучения турбулентных струйных течений обусловлена тем, что для решения многих прикладных задач ракетно-космической техники (обеспечение прочностных характеристик стартовых устройств, разделение ступеней ракет, определение акустических полей, создаваемых летательными аппаратами (ЛА) и т.д.) требуется знание полей газодинамических параметров струй, истекающих из двигателей. Процесс истечения сопровождается во многих случаях догоранием продуктов неполного окисления в окружающей среде и фазовыми переходами.

Предлагаемое пособие сформировалось в результате многолетней работы автора в этой области при чтении лекций для студентов, аспирантов и инженеров, при проведении лабораторных работ и практических занятий.

Курс лекций содержит основные сведения из термодинамики смеси газов, в том числе при протекании химических реакций; основные уравнения газовой динамики, описывающие движение смеси газов; анализ существующих методов расчета и разработанный автором алгоритм расчета турбулентных струй с диффузионным факелом, истекающих в затопленное пространство или спутный поток.

В пособии приведены темы и задачи для практических занятий по определению параметров струйных течений.

При изложении материала предполагается, что читатель знаком с курсами высшей математики, физики, термодинамики и гидрогазоаэродинамики ЛА.

Автор надеется, что указанное пособие будет полезным не только для студентов, магистрантов и аспирантов, но и для преподавателей, читающих лекции и проводящих практические занятия в области ракетно-космической и авиационной техники.

1. Основные сведения из термодинамики
смесей газов

1.1. Основные понятия и определения

Рассмотрим смесь, состоящую из q компонентов, в основном находящихся в газовой фазе. Возможно содержание в смеси небольшого количества твердых частиц.

Количественные соотношения компонентов, составляющих смесь, могут быть заданы массовыми, объемными или мольными долями.

Массовой долей называется отношение массы i-го компонента к массе смеси.Обозначая массовые доли буквой z, имеем

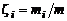, (1.1.1)

где 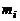– масса i-го компонента в смеси, m – масса смеси. При этом выполняются соотношения

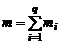, (1.1.2)

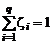. (1.1.3)

Массовые доли обычно задаются в процентах. Например, для воздуха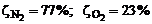

Объемной долей называется отношение приведенного объема газа к полному объему смеси. Под приведенными объемами газов, составляющих смесь, подразумеваются их объемы при давлении p и температуре T смеси. Предполагается, что объемом твердых частиц можно пренебречь по сравнению с объемом, занимаемым смесью.

Обозначая объемную долю i-го газа буквой 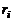, имеем

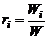, (1.1.4)

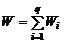, (1.1.5)

где W – объем смеси, 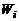– приведенный объем i-го газа.

Очевидно, что 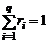(1.1.6)

Например, объемный состав воздуха в процентах: .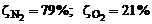

Мольной долей называется отношение числа молей i-го компонента к числу молей смеси.

Моль – количество вещества, в котором содержится столько же атомов или молекул, сколько атомов углерода в 0,012 кг углерода ¹²С. Число молекул в 1 моле называется постоянной Авогадро: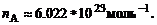

Количество вещества или число молей n, содержащихся в данной массе вещества m, определяется по формуле

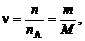(1.1.7)

где n – число молекул вещества, M – молярная масса (масса одного моля вещества, равная массе 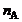молекул данного вещества).

Масса молекулы

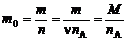. (1.1.8)

Обозначим число молей i-го компонента через 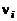, а смеси в целом через 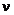. Тогда мольная доля i-го компонента 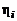определяется выражением

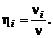(1.1.9)

Очевидно, что

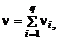(1.1.10)

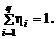(1.1.11)

Рассчитывая состав и термодинамические характеристики смеси в турбулентных струях, удобно пользоваться условной формулой смеси вида 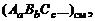где 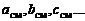– число молей компонентов A,B,C... в 1кг смеси. Например, условная формула воздуха .

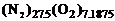Применение условной формулы позволяет единообразно задавать состав смеси как при наличии, так и при отсутствии химических реакций. В струях с физико-химическими превращениями меняется состав, но не меняется массовая концентрация химических элементов в реакциях и фазовых переходах. Поэтому, если в условной формуле 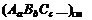под 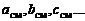понимать число молей химических элементов A,B,C... в 1 кг смеси, то условная формула для элементного состава не меняется даже в том случае, когда меняется компонентный состав. 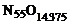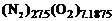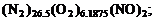Так, например, условной формуле для элементного состава соответствуют различные условные формулы для компонентных составов: ; 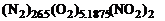и т.д.

Определение состава смеси в турбулентной струе при смешении без химических реакций.При расчете смешения турбулентных одиночных или блочных струй с окружающей средой будем полагать, что составы продуктов сгорания топлива для всех двигателей блока одинаковы. Тогда можно ввести параметр смешения y, понимая под ним массовую долю вещества струи в смеси. Если окрасить продукты сгорания топлива в черный цвет, а среду, в которую они истекают, в белый, то в таком мысленном эксперименте значение y будет равно отношению массы черного вещества к общей массе смеси.

Использование параметра смешения позволяет выразить состав смеси при заданных значениях концентраций компонентов на срезах сопл 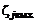и в окружающей среде 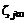через одну переменную y, меняющуюся по своему физическому смыслу в пределах :

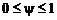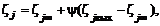(1.1.12)

где 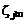– массовая концентрация j-го компонента в окружающей среде, 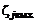– массовая концентрация j-го компонента на срезах сопл, 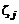– массовая концентрация j-го компонента в смеси.
Состав смеси будет полностью определен, если задать q-1 уравнений типа (1.1.12), где q – число компонентов в смеси, и использовать очевидное замыкающее соотношение

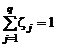. (1.1.13)

Определение состава смеси в турбулентной струе при термодинамически равновесном истечении.В струях с физико-химическими превращениями принимается допущение о неизменности элементного состава продуктов сгорания топлива всех двигателей блока. Так как элементный состав при химических реакциях в процессе смешения с окружающей средой не меняется, то, по аналогии с формулами (1.1.12) и (1.1.13), его можно выразить через параметр смешения Y и элементные составы продуктов сгорания топлива и окружающей среды:

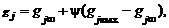(1.1.14)

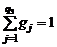, (1.1.15)

где 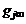– массовая концентрация j-го химического элемента в окружающей среде, – массовая концентрация j-го химического элемента на срезах сопл, 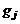– массовая концентрация j-го химического элемента в смеси, 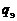– число химических элементов в смеси.

Соответственно, условная формула смеси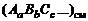
выражается через условные формулы топлива 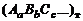и окружающей среды 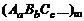соотношениями

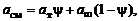
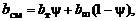(1.1.16)

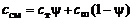и т.д.,

где a_см , b_см , c_см ... – число молей химических элементов A, B, C... в 1 кг смеси.

Для определения состава компонентов смеси требуется введение дополнительной процедуры – термодинамического расчета. Входными данными в этой процедуре являются параметр смешения Y, однозначно определяющий условную формулу смеси или ее массовый элементный состав, температура T и давление p, равное на изобарическом участке струи давлению окружающей среды: 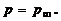Два параметра из трех – y и T – меняются по длине и сечению струи и поэтому задаются наборами значений, составленных следующим образом.

Параметр смешения Y меняется в пределах 0 £ y £ 1. Отсюда следует, что набор y должен содержать 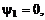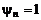и несколько промежуточных значений y_j. Шаг по параметру смешения 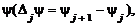который может быть как постоянным, так и переменным, выбирается из условия достижения требуемой точности линейной интерполяции результатов термодинамического расчета для величин Ψ, не совпадающих с узловыми точками y_j . Расчеты струйных течений показали, что достаточная точность достигается при количестве значений 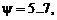если удачно подобрать узловые точки. Рекомендуется, помимо 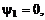и 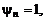задать несколько значений вблизи величины 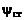, где 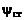– значение y, при котором достигается стехиометрическое соотношение, т.е. в смеси находится ровно столько окислителя и горючего, сколько требуется для полного сгорания. Например, в смеси с условной формулой 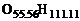имеет место стехиометрическое соотношение горючего и окислителя, т.е. при полном сгорании в смеси будет содержаться только продукт полного окисления – пары воды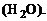

Степень отличия действительного соотношения компонентов смеси от стехиометрического оценивают коэффициентом избытка окислителяa, который определяют по формуле

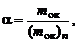(1.1.17)

где 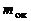– масса окислителя в смеси, 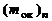– масса окислителя, которая требуется для полного сгорания горючего.

Если наблюдается недостаток окислителя против теоретически необходимого количества, т.е. 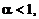то в турбулентной струе происходит диффузионное догорание продуктов неполного окисления при смешении с окружающей средой.

Диапазон изменения температур выбирается с некоторым запасом, обеспечивающим попадание рассчитываемых значений статических температур T и температур торможения 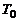во всех точках струи внутрь этого диапазона. В интервале температур 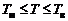, где 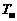– нижняя, а 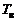– верхняя границы, задаются 5...20 значений 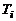, обеспечивающих нужную точность аппроксимации результатов термодинамического расчета. Все сочетания выбранных значени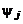й и 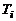составляют, при известном 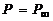, набор исходных данных для проведения серии термодинамических расчетов и подготовки массивов входных параметров в программы расчета изобарических участков турбулентных струй.

1.2. Понятие термодинамического равновесия. Температура, давление, внутренняя энергия, энтальпия (теплосодержание) и энтропия смеси идеальных газов

Состоянием термодинамического равновесия мы будем называть такое состояние, в которое с течением времени приходит система, находящаяся при определенных неизменных внешних условиях. Газ в равновесном состоянии может пребывать сколь угодно долго, пока не изменятся воспринимаемые им внешние воздействия (состояние внешней среды).

Если в каждой жидкой частице – аналоге материальной точки в механике – наблюдается термодинамическое равновесие, то вся среда называется термодинамически равновесной. При этом выполняется условие

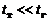, (1.2.1)

где 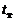– время установления термодинамического равновесия в жидкой частице; 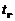– характерное газодинамическое время, т.е. время, в течение которого заметно изменяются внешние условия.

Итак, термодинамически равновесными называются процессы, в которых газ, изменяясь, проходит через равновесные состояния. Очевидно, что в полной мере равновесные процессы неосуществимы, так как основание для возникновения всякого процесса есть нарушение равновесия системы. Равновесный процесс можно представить как предельный для процессов, в которых газ проходит через отдельные состояния, настолько мало отличающихся от равновесных, что их можно практически принимать за равновесные.

Процессы, происходящие в турбулентных струях, как дозвуковых, так и сверхзвуковых, в большинстве случаев можно считать равновесными.

Для термодинамически равновесного газа можно ввести понятие давления р и температуры T. Сделаем это, пользуясь основными положениями молекулярно-кинетической теории.

Введем понятие идеального газа. Идеальный газ – газ, в котором молекулы взаимодействуют только при столкновениях и собственный объем молекул пренебрежимо мал по сравнению с объемом, занимаемым газом (при достаточном разрежении все газы можно считать идеальными).

В дальнейшем предполагается, что турбулентные струи представляют собой смесь идеальных газов.

Для идеального газа справедливо уравнение

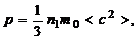(1.2.2)

где р – давление газа, n₁ – концентрация молекул (число молекул в единице объема), c – скорость хаотического теплового движения молекул, < > – знак математического ожидания случайной величины.

Давление идеального газа, выраженное через среднюю кинетическую энергию молекул:

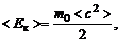(1.2.3)

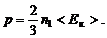(1.2.4)

Температура вводится как мера средней кинетической энергии хаотического движения молекул:

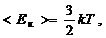(1.2.5)

где k – постоянная Больцмана, ,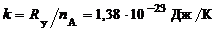

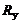– универсальная газовая постоянная, 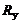=8,314 Дж/(моль∙К). Подставляя в (1.2.4) соотношение (1.2.5) и учитывая, что 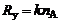, получим

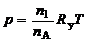. (1.2.6)

Помножим числитель и знаменатель в правой части (1.2.6) на массу молекулы 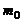и, принимая во внимание, что 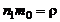, где 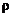– плотность газа (масса единицы объема), а 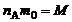(см. соотношение (1.1.8)), приходим к уравнению состояния идеального газа (уравнение Менделеева-Клапейрона):

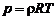, (1.2.7)

где 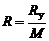; R [Дж/кг∙К]. (1.2.8)

Закон Дальтона для давления р смеси идеальных газов:

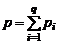, (1.2.9)

где q – число газов, 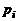– парциальное давление i-го газа, т.е. давление, которое оказывал бы i-й газ при отсутствии других газов, составляющих смесь.

Закон Авогадро: при одинаковых физических условиях (одинаковых давлениях р и температурах T) в равных объемах различных газов содержится одинаковое количество молекул.

Опираясь на уравнение состояния, закон Дальтона и закон Авогадро, найдем связь между массовыми, мольными и объемными долями газов, входящих в смесь.

Следствием закона Авогадро является утверждение, что мольные доли 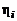(см. (1.1.9)) численно равны объемным долям 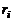(см. (1.1.4)):

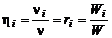. (1.2.10)

Из определения массовых долей (см. (1.1.1)) следует:

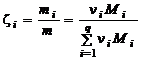. (1.2.11)

Разделив (1.2.11) на общее число молей 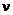, содержащихся в смеси, с учетом (1.2.10) получим уравнение, позволяющее вычислить массовые доли по известным объемным долям:

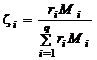. (1.2.12)

Для вывода соотношения между объемными и массовыми долями возьмем уравнения (1.2.10) и (1.1.7):

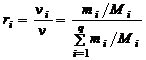. (1.2.13)

Разделив (1.2.13) на массу смеси m с учетом (1.1.1), получим

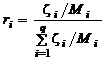. (1.2.14)

Кажущаяся молярная масса. Из определения моля газа следует, что молярная масса i-го газа в смеси равна:

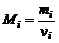. (1.2.15)

Обозначая по аналогии отношение 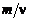для смеси через М_к, находим

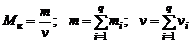. (1.2.16)

Величина М_к называется кажущейся молярной массой смеси. Для вычисления М_к напишем соотношение

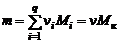. (1.2.17)

Разделим (1.2.17) на величину 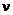и учтем соотношение (1.2.13). Тогда

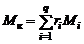. (1.2.18)

Формула (1.2.18) показывает, что кажущаяся молярная масса равна сумме произведений молярных масс отдельных газов, составляющих смесь, на их объемные доли.

Газовая постоянная смеси.Умножим правую и левую части (1.2.7) на объем W и запишем уравнение состояния для смеси в виде

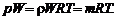(1.2.19)

Уравнение состояния для отдельных газов, входящих в смесь:

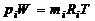. (1.2.20)

Просуммировав почленно уравнения состояния газов, найдем

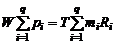(1.2.21)

или, с учетом закона Дальтона (1.2.9),

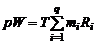. (1.2.22)

Из сравнения этого уравнения с уравнением состояния смеси (1.2.19) имеем

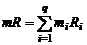, (1.2.23)

откуда

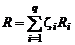. (1.2.24)

Формула (1.2.24) показывает, что газовая постоянная смеси газов равна сумме произведений газовых постоянных отдельных газов на их массовые доли.

Если смесь задана объемными долям, то выразим массовые доли через объемные с помощью зависимостей (1.2.12) и (1.2.18)

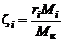. (1.2.25)

Подставляя (1.2.25) и (1.2.8) в (1.2.24), получим

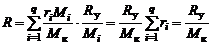. (1.2.26)

Формула показывает, что как газовая постоянная отдельного газа, входящего в смесь, так и газовая постоянная смеси газов определяются по одной и той же формуле, в которую для газа подставляется его молярная масса, а для смеси - ее кажущаяся молярная масса.

Парциальное давление.Для определения парциального давления газа напишем уравнения состояния этого газа и смеси в целом:

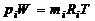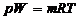, , (1.2.27)

откуда после почленного деления получим

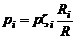. (1.2.28)

Парциальное давление газа при задании смеси объемными долями определим следующим образом. Напишем два уравнения состояния для i-го газа, из которых первое будет относиться к его состоянию в смеси, когда он имеет парциальное давление p_i и занимает полный объем W, а второе - к приведенному состоянию, когда давление будет равно давлению смеси p, которому соответствует приведенный объем газа W_i :

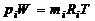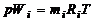, . (1.2.29)

Разделив первое уравнение (1.2.29) на второе, получим

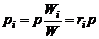. (1.2.30)

Парциальное давление отдельного газа равно полному давлению смеси, умноженному на объемную долю этого газа.

Внутренняя энергия газа складывается из внутренних кинетической и потенциальной энергий. Обозначим внутреннюю энергию единицы массы через u.

Внутренняя кинетическая энергия 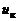– совокупность кинетических энергий поступательного и вращательного движения молекул, энергии колебательного движения атомов, составляющих молекулы, и энергии внутриатомного движения. Внутренняя кинетическая энергия зависит от температуры Т и возрастает при ее увеличении.

Внутренняя потенциальная энергия 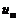определяется силами межмолекулярного взаимодействия и потенциальной энергией атомов. Внутренняя потенциальная энергия зависит от расстояния между молекулами, а следовательно, и от объема, занимаемого газом.

Таким образом, внутренняя энергия будет функцией от двух независимых параметров, например, температуры Т и удельного объема w (удельный объем – объем единицы массы газа).

Запишем полный дифференциал:

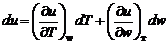. (1.2.31)

Идеальные газы из-за отсутствия потенциальных сил взаимодействия молекул обладают лишь внутренней кинетической энергией. Тогда для идеального газа

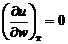и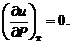

Поскольку в процессе постоянного объема работа не совершается, то в нем теплота, сообщаемая газу, идет на увеличение его внутренней энергии:

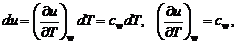(1.2.32)

где 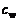– удельная теплоемкость при постоянном объеме (удельная теплоемкость c – количество тепла, которое надо сообщить единице массы газа для повышения его температуры на 1°К).

Отсюда следует, что для идеального газа

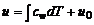. (1.2.33)

Заметим, что величина внутренней энергии определяется с точностью до произвольной постоянной. Однако этот факт для термодинамических расчетов не имеет значения, так как в них вычисляется не абсолютная величина u, а ее изменение.

Внутренняя энергия смеси газов определяется как сумма произведений массовых долей компонентов смеси на их внутренние энергии:

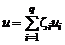. (1.2.34)

Теплосодержание (энтальпия).В термодинамике во многих случаях, особенно когда независимыми параметрами являются давление р и температура Т,применяется функция состояния h, называемая теплосодержанием или энтальпией, которая связывает величины u, р, w соотношением

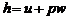. (1.2.35)

В соответствии с первым началом термодинамики

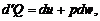(1.2.36)

где Q – количество подведенного к единице массы тепл; штрих в выражении 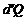означает, что 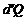не является полным дифференциалом.

Примем в уравнении (1.2.36) давление р постоянным. Тогда

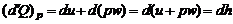. (1.2.37)

Учтем, что удельная теплоемкость при постоянном давлении определяется зависимостью

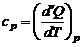. (1.2.38)

Из (1.2.37) и (1.2.38) следует, что величина теплосодержания для идеального газа находится из уравнения

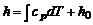. (1.2.39)

Так же как и внутренняя энергия, теплосодержание определяется с точностью до произвольной постоянной.

Широкое распространение получила система отсчета теплосодержаний, в которой в величину h вносятся стандартная теплота образования и теплоты фазовых и полиморфных превращений. Обозначим таким образом найденное теплосодержание через h_п. Тогда теплосодержание 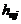j-го химического соединения (компонента) определится по формуле

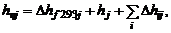(1.2.40)

где для этого компонента заданы: 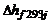– стандартная теплота образования, физическое теплосодержание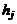

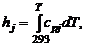(1.2.41)

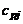– удельная теплоемкость при постоянном давлении, 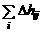– теплоты фазовых и полиморфных превращений. Для жидких и твердых веществ при постоянном значении их теплоемкостей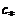

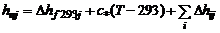. (1.2.42)

Теплоту образования 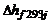находят при образовании веществ из элементов в стандартном состоянии, т.е. при давлении р=1,02 бар и температуре Т=293,15 К. Стандартными элементами являются газы 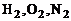и др., твердый углерод С и металлы.

Удобство использования такой системы отсчета теплосодержаний состоит в том, что на величину суммарного теплосодержания смеси 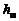, которое определяется по уравнению

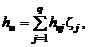(1.2.43)

не влияют физико-химические превращения. Величины 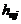приводятся в таблицах, или для их определения задаются аппроксимирующие полиномы.

Показатель адиабаты смеси 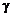находится как отношение

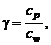(1.2.44)

где удельную теплоемкость при постоянном давлении 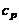удобно определять как производную от теплосодержания по температуре при фиксированном значении р:

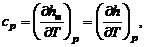(1.2.45)

а удельную теплоемкость при постоянном объеме 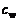для идеального газа находить по формуле Майера

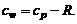(1.2.46)

Энтропия.Важной функцией состояния, позволяющей судить о направлении термодинамического процесса, является энтропия. Обозначим энтропию, отнесенную к единице массы, через S. Энтропия определяется соотношением

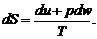(1.2.47)

Интегрируя уравнение (1.2.47) с использованием зависимостей (1.2.32), (1.2.7) и учитывая, что 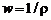, получим

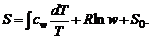(1.2.48)

Выражая в (1.2.47) внутреннюю энергию через теплосодержание h (см. (1.2.35)), получим

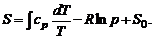(1.2.49)

В соотношениях (1.2.48) и (1.2.49) 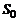– постоянная интегрирования.

Для калорически совершенного газа ( 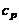и 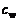постоянны)

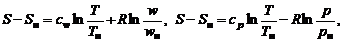(1.2.50)

где 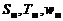и 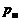соответствуют некоторому начальному состоянию.

Энтропия смеси газов равна:

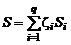. (1.2.51)

Уравнение неразрывности

Применительно к некоторой массе жидкости или газа, занимающего произвольно выделенный объем, закон сохранения массы можно сформулировать в следующем виде: масса жидкости или газа, состоящая из одних и тех же частиц, в процессе движения остается постоянной.

Естественно предполагается, что скорости движения жидких частиц значительно меньше скорости света, а это позволяет пренебречь релятивистскими эффектами изменения массы.

Движение жидких частиц будем рассматривать в трехмерном ортогональном пространстве с декартовыми координатами 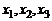и единичными ортами 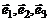.Слово «ортогональность» означает взаимную перпендикулярность координатных осей.

Используем часто применяемые в современной физической и математической литературе правила, позволяющие упростить запись: каждый буквенный индекс, встречающийся в выражении один раз, может принимать значения 1, 2, 3.

При этом, поскольку для обозначения координатных осей выбраны буквы с индексами (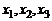), под записью 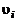, например, будем понимать совокупность трех проекций скорости 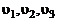; запись 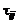означает совокупность 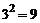величин: .

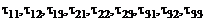По дважды повторяющемуся в одночлене индексу (за немногими, всегда оговариваемыми случаями) следует производить суммирование от 1 до 3.

Таким образом, выражения 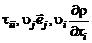означают:

,

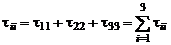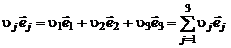, (2.1.1)

.

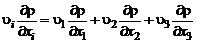Индексы суммирования часто называются «немыми» в том смысле, что сумма, очевидно, не меняет значение, если заменить «немой» индекс другой буквой: 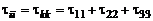и т.д.

Во избежание путаницы в обозначениях индексы, относящиеся к химическому элементу или соединению, там, где это необходимо, будем для векторных и тензорных величин ставить вверху.

Так, например, выражение 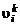может обозначать проекцию скорости k-го химического компонента на ось .

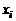Скалярные величины, такие как плотность, температура, давление и т.д., поскольку они инвариантны по отношению к любому преобразованию координат, для химических соединений или элементов обозначаем, как и ранее, индексом внизу. Например, 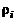– плотность i-го компонента смеси.

Приняв во внимание сделанные замечания, перейдем к математической записи закона сохранения массы для смеси газов.

Плотность смеси найдем по формуле

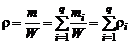. (2.1.2)

Скорость жидкой частицы 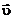определим как среднемассовую скорость всех компонентов, составляющих смесь:

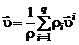. (2.1.3)

Масса газа, заключенная в объеме W и ограниченная замкнутой поверхностью S,равна:

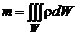. (2.1.4)

Будем считать, что внутри выделенного объема нет источников и стоков, через которые газ мог бы подаваться в заданный объем или извлекаться из него. Тогда масса газа, находившегося внутри объема W в момент времени t, в последующие моменты времени, в соответствии с законом сохранения массы, останется неизменной. Конечно при этом нужно учитывать смещение граничной поверхности S из-за движения граничных жидких частиц.

Итак, в момент времени t масса газа внутри объема W равна:

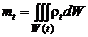. (2.1.5)

За промежуток времени 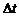подынтегральная функция 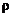и объем W,занятый выделенными жидкими частицами, получили приращения:

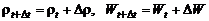. (2.1.6)

Подставляя соотношения (2.1.6) в (2.1.4), получим

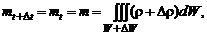
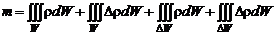. (2.1.7)

Изменение объема 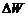, связанное с перемещением за время 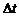граничной поверхности, равно:

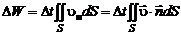, (2.1.8)

где 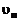– проекция скорости граничных жидких частиц на внешнюю (направленную из объема) нормаль к поверхности S.

С учетом формулы (2.1.8) выражения для интегралов по объему 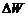запишутся в виде

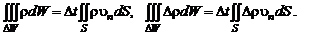(2.1.9)

Так как масса газа m не меняется с течением времени, то полная производная по времени равна нулю:

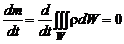. (2.1.10)

По определению производной,

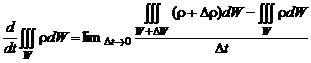. (2.1.11)

Подставляя в (2.1.11) зависимости (2.1.7) и (2.1.9) и переходя к пределу при 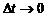, получим интегральную форму записи закона сохранения массы:

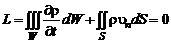. (2.1.12)

В частном случае установившегося движения, когда параметры газа в каждой фиксированной точке пространства не ме