Построение эпюр Q и М для балок на двух опорах.

Решение балок на двух опорах начинают с определения опорных реакций, а затем идут с любого конца балки.

Пример 5.3.

Для балки, изображённой на рис.27, построить эпюры Q и М, если F = 2 кН; m = 4 кНм; q = 1 кН/м.

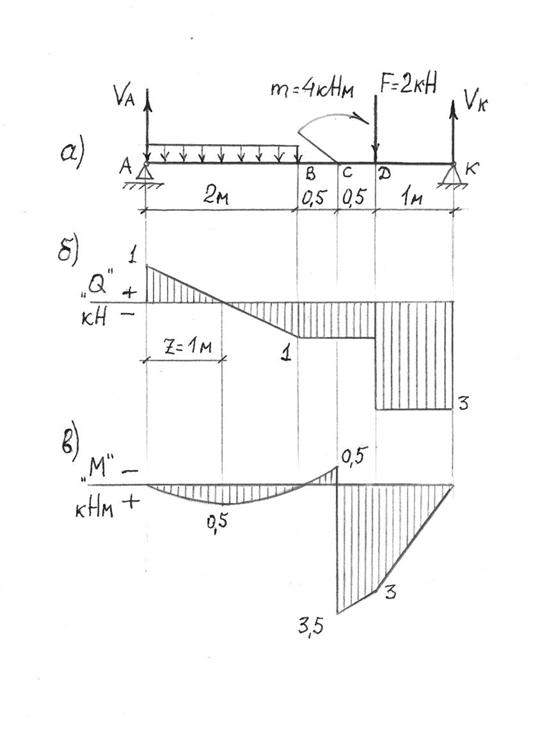
рис. 27

1) Определяем опорные реакции

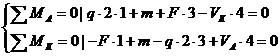
V_K = 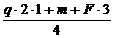= 3 кН

V_A = 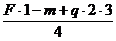= 1 кН

Проверка: åF_Y = 0

-q ^. 2 + V_A – F + V_K = 0

-2 + 1 – 2 + 3 = 0

0=0

2) Строим эпюру Q (рис.27б).

На незагруженных участках эпюра Q постоянна – достаточно определить одно значение.

Q_ДК = -V_K = -3 кН

Q_СД = -V_K + F = -3 + 2 = -1 кН

Q_ВС = -V_K + F = -1 кН

На загруженном участке определяют значения поперечной силы в начале и в конце участка.

Q_А^пр = V_A = 1 кН

Q_В^лев = V_A – q ^. 2 = 1 – 2 = -1 кН

3) Строим эпюру М (рис.27в) (при направлении справа налево).

M_K = 0

M_Д = V_K ^. 1 = 3 кНм

М_С^пр = V_K ^. 1,5 – F ^. 0,5 = 3 ^. 1,5 – 2 ^. 0,5 = 3,5 кНм

М_С^лев = V_K ^. 1,5 – F ^. 0,5 – m = -0,5 кНм

М_В = V_K ^. 2 – F ^. 1 – m = 3 ^. 2 – 2 ^. 1 – 4 = 0

Как видно из эпюры Q значение абсциссы Z, при котором Q = 0, равняется 1 м. Необходимо определить момент в сечении Z = 1 м.

М_Z = V_A ^. Z – q ^. Z 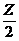^. = 1 ^. 1 – 1 ^. 1 ^. 0,5 = 0,5 кНм

На загруженном участке АВ эпюра М очерчивается параболой, вершина которой в сечении Z = 1, на незагруженных участках эпюра М очерчивается наклонными линиями.

4) Опасным является сечение С, где действует максимальный по абсолютной величине изгибающий момент М_МАХ = 3,5 кНм

Подбор сечений при изгибе

Подбор сечений при изгибе (условия работы нормальные) производят по формуле:

W_X ≥ 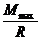, где

W_X – требуемый момент сопротивления, геометрическая характеристика сечения балки, от которой зависит её прочность. Чем больше момент сопротивления, тем балка прочнее.

M_max – максимальный по абсолютной величине изгибающий момент, берётся с эпюры М.

R – расчётное сопротивление материала балки растяжению (сжатию) при изгибе (МПа). берётся из таблиц.

Задача 5

На балку действуют нормативная равномерно распределённая нагрузка q_n с коэффициентами надёжности γf₁ = 1,4 и нагрузка F_n c коэффициентом γf₂ = 1,2 (рис.28)

1) Определить расчётное значение нагрузок, если q_n = 6 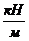; F_n = 60 кН

2) Построить от них эпюры Q и М.

3) Подобрать сечение прокатного двутавра из условия прочности, если R = 240 МПа. Условия работы нормальные.

4) Проверить прочность подобранного сечения на сдвиг, если R_S = 140 МПа.

5) Вычислить наибольший прогиб балки ¦_max и проверить её жёсткость в случае, если 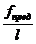= 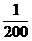, а Е_стали = 2,06 ^. 10⁵ МПа.

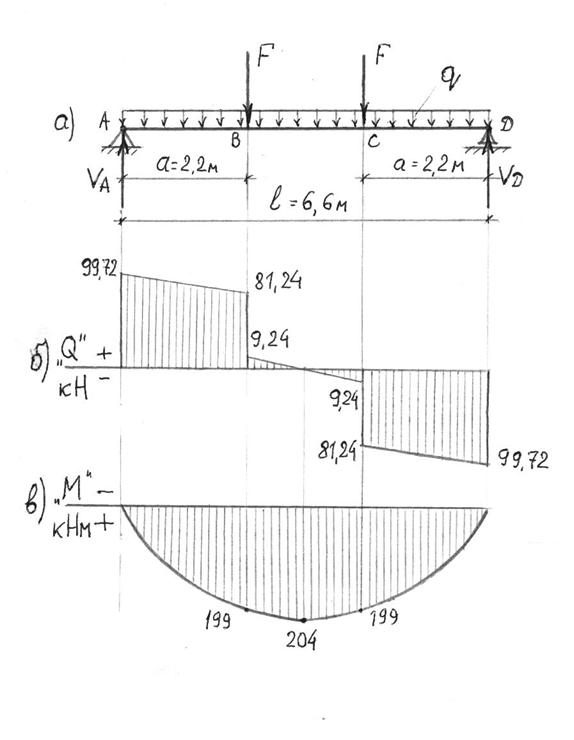
рис. 28

Решение:

1) Определяем расчётные значения нагрузок.

q = q_n ^. γf₁ = 6 ^. 1,4 = 8,4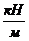

F = F_n ^. γf₂ = 60 ^. 1,2 = 72 кН

2) Определяем опорные реакции. Так как опоры в равных условиях то опорные реакции равны

V_A = V_Д = 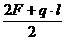= = 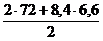99,72 кН

3) Строим эпюру Q (рис. 28б).

Q_A^пр = V_A = 99,72 кН

Q_B^лев = V_A – q ^. 2,2 = 99,72 – 8,4 ^. 2,2 = 81,24 кН

Q_B^пр = V^A – q ^. 2,2 – F = 99,72 – 8,4 ^. 2,2 – 72 = 9,24 кН;

Q_C^лев = V_A – F – q ^. 4,4 = 99,72 – 72 – 8,4 ^. 4,4 = -9,24 кН;

Q_C^пр = V_A – 2 ^. F – q ^. 4,4 = 99,72 – 2 ^. 72 – 8,4 ^. 4,4 = -81,24 кН;

Q_Д^лев = -V_Д = -99,72 Кн.

Сечение, в котором Q=0, находится в середине пролёта, т.е. Z = 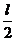= 3,3 м

4) Строим эпюру “М” (рис.28в).

М_А = 0;

M_B = M_C = V_A ^. 2,2 – q ^. 2,2 ^. 1,1 = 199 кНм.

Для построения параболы необходимо промежуточное значение момента при Z = 3,3 м

М_К = V_A ^. 3,3 – F ^. 1,1 – q ^. 3,3 ^. = 204 кНм;

М_Д = 0.

Эпюра “M” имеет криволинейное очертание, выпуклостью вниз.

5) Подбираем сечение двутавра.

Максимальный изгибающий момент.

М_max = 204 кНм = 204 ^. 10^-3 МН;

R = 240 Мпа = 240 .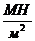

Требуемый момент сопротивления.

W_X 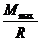³ ³ 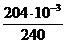= 850 ^. 10^-6 м³ = 850 см³.

По сортаменту (ГОСТ 8239 – 89) выбираем двутавр № 40 с W_X^табл = 953 см³ > 850 см³.

Так как подобранное сечение требуется проверить на сдвиг, выписываем из той же таблицы данные, необходимые для подсчёта наибольших касательных напряжений: S_X^табл = 545 см³; J_X^табл = 19062 см⁴; d = 0,83 см.

Расчёт производится по максимальной поперечной силе Q_max = 99,72 кН.

Условие прочности на сдвиг.

τ = 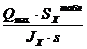≤ R_S;

Q_max = 99,72 кН = 99,72 ^. 10^-3 МН;

S_X^табл = 545 см³ = 545 ^. 10^-6 м³;

J_X^табл = 19062 см⁴ = 19062 ^. 10^-8 м⁴;

s = 0,83 см = 0,83 ^. 10^-2 м.

τ_max = 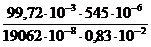= 34 Мпа < R_S = 140 МПа.

Стенка имеет значительный запас прочности на сдвиг.

6) Определяем наибольший прогиб балки, пользуясь табличными данными (приложение табл. 3).

Расчёт ведём по нормативной нагрузке.

ƒ_max = ƒ_к = ƒ_2F + ƒ_q = + ^. ;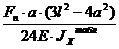

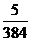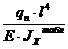ƒ_max = + ^. ;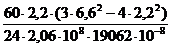

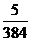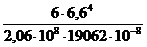где Е = 2,06 ^. 10⁵ МПа = 2,06 ^. 10⁸ кПа.

Получаем ƒ_max = 0,019 м.

7) Проверяем жёсткость балки.

Условие жёсткости.

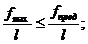
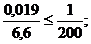
0,0029 < 0,0050 - балка жёсткая!

ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ

Задача 1.Определить усилия в стержнях фермы методом вырезания узлов (аналитически). Данные для задачи своего варианта взять из таблицы 2 и схемы на рис.29.

Строка
F, кН
F1, кН
h, м		3,5	4,5		3,5	4,5			3,5	4,5
d, м

Таблица 2

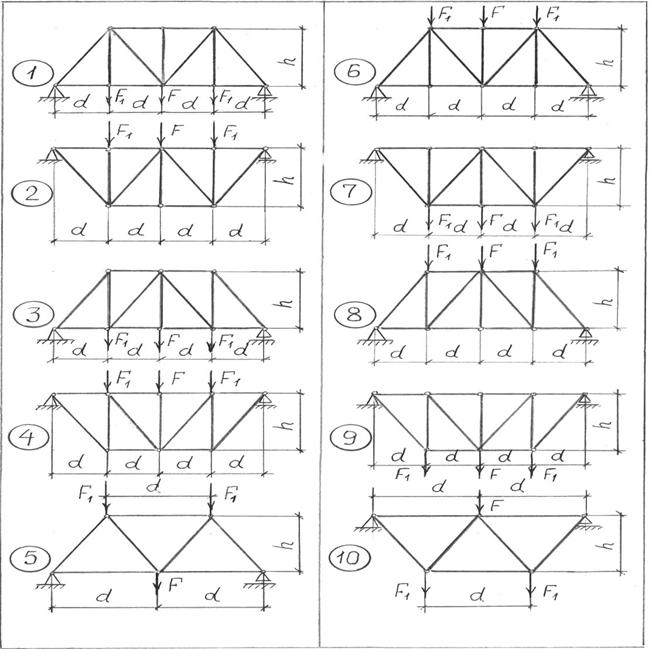
рис.29

Задача 2.Найти опорные реакции балки, нагруженной, как показано по рис.30. Данные для задачи своего варианта взять из таблицы 3.

Строка
F, кН
q, кН/м
m, кНм
α, град.
а1, м			1,5				3,5			1,5
а2, м			1,5				1,5			1,5
а3, м		1,5	3,5

Таблица 3

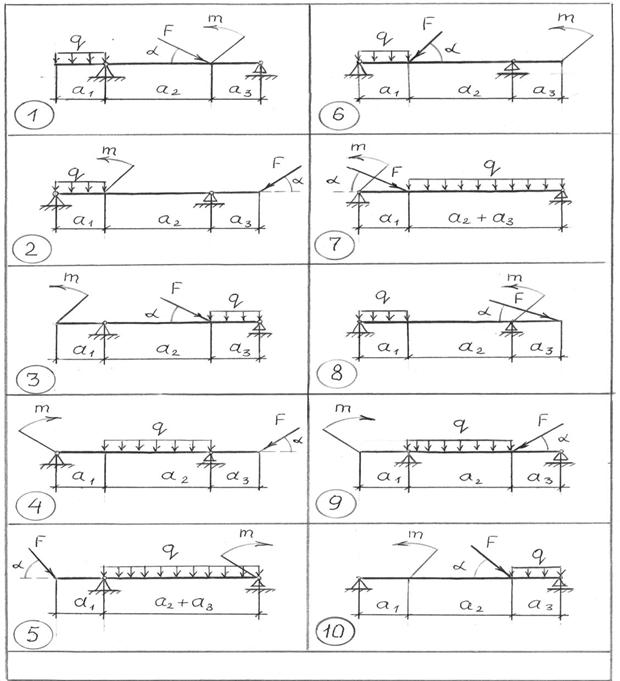
рис.30

Задача 3.Определить положение центра тяжести сечения, составленного из прокатных профилей. Данные для задачи своего варианта взять из таблицы 4 и рис.31.

Вариант задачи определить по двум последним цифрам шифра.

Схема	Вариант	Двутавр №	Щвеллер №	Полоса b x h, мм	Схема	Вариант	Двутавр №	Щвеллер №	Полоса b x h, мм
I				220x14	VI				220x14
			220x12				200x12
			180x14				160x12
			150x10				150x10
			240x12				150x8
			200x10				140x8
			200x10				160x10
			180x12				200x10
			220x10				260x12
			220x12				280x12
II				80x6	VII				260x14
			100x8				240x10
			160x10				240x14
			200x10				220x10
			150x10				220x12
			100x8				200x10
			120x10				200x12
			180x12				180x10
			150x10				180x10
			180x10				120x8
III				100x8	VIII			___	120x8
			120x8			___	120x10
			160x10			___	120x10
			160x12			___	140x12
			150x10			___	150x10
			200x10			___	160x12
			200x12			___	120x10
			220x12			___	140x12
			220x10			___	100x8
			240x12			___	100x10
IV				300x14	IX		___		220x10
			240x12		___		200x10
			220x12		___		160x10
			200x10		___		150x12
			200x12		___		150x10
			180x12		___		160x12
			140x10		___		200x12
			120x10		___		260x10
			200x12		___		280x14
			180x10		___		140x8
V				250x12	X				220x10
			220x12				100x8
			200x12				120x8
			150x10				160x10
			150x12				160x12
			120x10				150x10
			200x10				200x10
			180x12				200x12
			180x12				220x12
			140x10				240x10

Таблица 4

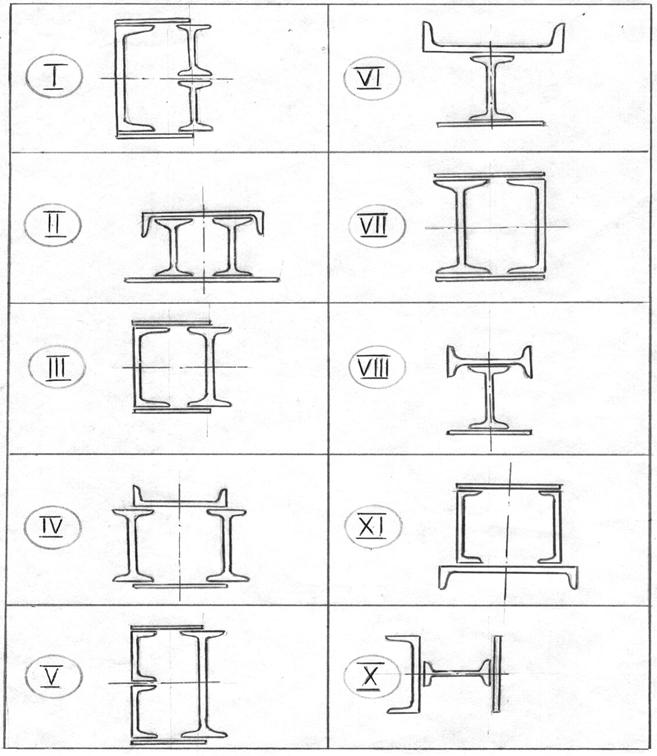
рис.31

Задача 4.Для ступенчатого стального бруса:

1. Построить эпюру продольной силы N.

2. Подобрать площадь поперечного сечения А при расчетном сопротивлении материала R=240 МПа.

3. В соответствии с принятой площадью построить эпюру нормальных напряжений s.

4. Определить абсолютную деформацию бруса, если Е=2 ^. 10⁵ МПа.

Данные для задачи своего варианта взять из таблицы 5 и рис.32.

Строка
F1, кН
F2, кН
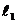, м		1,2	1,4	1,3		1,8	1,6	1,4	1,2	0,8
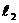, , м	1,2		1,2	1,4	1,1		1,2	1,4	0,8
, м		1,8	1,6	1,4	1,4	1,2	1,2		1,5

Таблица 5

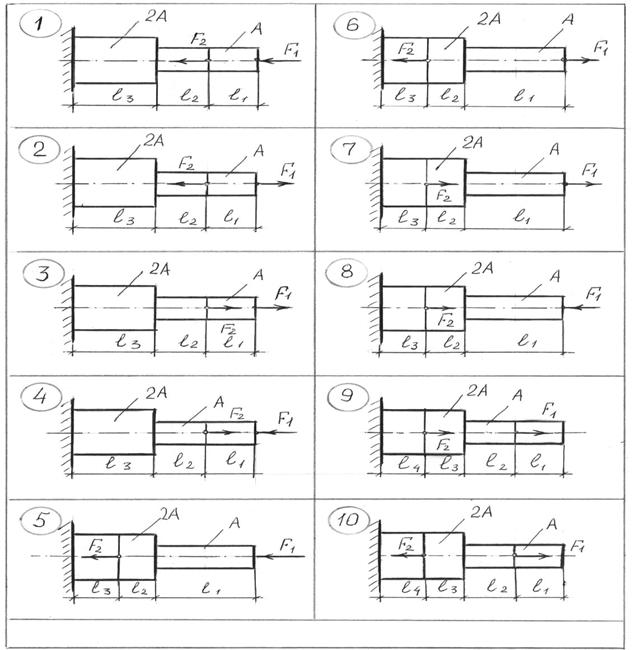
рис.32

Задача 5.

1. Построить эпюры Q и М.

2. Подобрать сечение прокатного двутавра из условия прочности, если R=240 МПа, условия работы – нормальные.

3. Проверить прочность подобранного сечения на сдвиг, если R_s=140 МПа.

Данные для задачи своего варианта взять из таблицы 6 и схемы на рис.33.

Строка
F, кН
m, кНм
q, кН/м
а, м	1,6			1,6	2,5		2,5	1,8		1,5
b, м	0,8			1,8		2,5
, м						4,5		4,6

Таблица 6

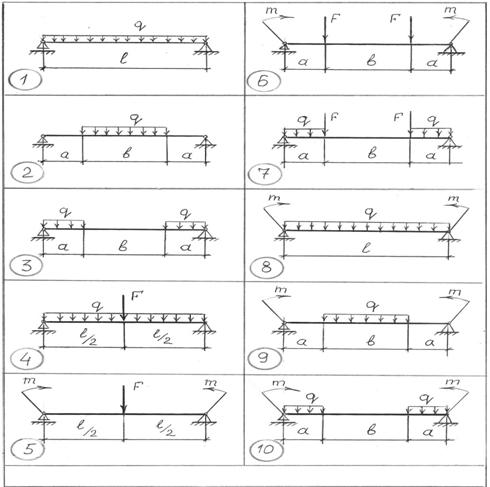
рис.33

ПРИЛОЖЕНИЯ

Приложение 1. СОРТАМЕНТ ПРОКАТНОЙ СТАЛИ

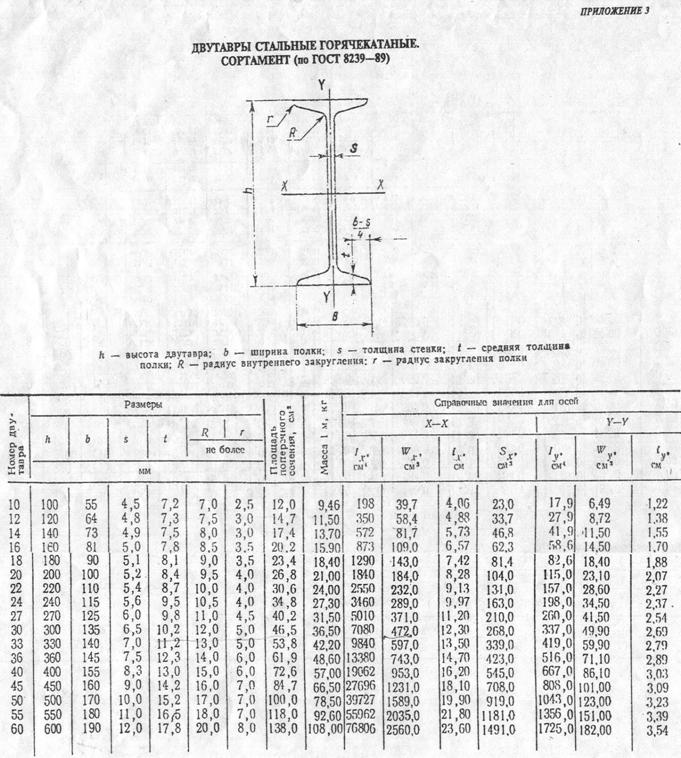
Приложение 2.СОРТАМЕНТ ПРОКАТНОЙ СТАЛИ

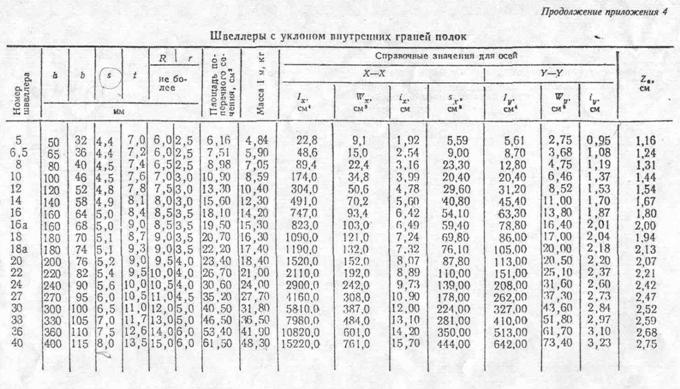
Литература

Основные источники:

1 Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов: Учеб. для средних проф. учеб. заведений / А.И. Аркуша. -7-е изд., стер. - М.: Высш.шк., 2008.

2 Сетков В.И. Техническая механика для строительных специальностей: уеб. пособие для студ. сред. Проф. образования / В.И.Сетков. -2-е изд., стер. - М.: Издательский центр «Академия», 2008.

3 Сетков В.И. Сборник задач по технической механике : учеб. пособие для студ. сред. проф. образования / В.И.Сетков. - 5-е изд. стер. - М.: Издательский центр «Академия», 2009.

4 Олофинская В.П. Детали машин. Краткий курс и тестовые задания: учеб. пособие. – 2-е изд. и доп. – М.6 ФОРУМ, 2008.

Дополнительные источники:

1 Сабодаш П.Ф. Техническая механика: Учебник для ссузов. - М.: Дрофа, 2004.

2 Вереина Л.И. Техническая механика: Учеб. для нач. проф. образования. - М.: Проф. обр-Издат, 2002.

3 Кочетов В.Т. Сопротивление материалов. / М.В. Сопротивление материалов. - Ростов-на-Дону, Феникс, 2001.

4 Сетков В.И. Техническая механика для строительных специальностей: уеб. пособие для студ. сред. Проф. образования / В.И.Сетков. -2-е изд., стер. - М.: Издательский центр «Академия», 2008.

5 Олофинская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: Учебное пособие. - М.: ФОРУМ: ИНФРА-М, 2005.

ГОСТ 8609 – 86 Сталь прокатная угловая равнополочная.

ГОСТ 8510 – 86 Сталь прокатная угловая неравнополочная.

ГОСТ 8510 – 86 Сталь прокатная – балки двутавровые.

ГОСТ 8240 – 72 Сталь прокатная – швеллеры.

СНиП II - 23-81*. Стальные конструкции. – М.: Стройиздат, 1984.

СН 528 – 80 Перечень единиц физических величин, подлежащих применению в строительстве. – М.: Стройиздат, 1981.