Основы корреляционно-регрессионного анализа

В общем случае степень связи между двумя переменными величинами можно характеризовать следующими зависимостями: независимая, стохастическая, корреляционная, функциональная.

Независимыми называются такие переменные величины, у которых при изменении одной величины другая остается постоянной.

Стохастически зависимые – это такие величины, у которых каждому значению одной величины соответствуют различные значения другой, которые являются случайными и могут быть описаны законами распределения.

Корреляционная зависимость – частный случай стохастической, каждому значению одной величины соответствуют различные средние значения другой.

Функционально зависимыми называются такие величины, у которых каждому значению одной величины соответствует вполне определенное значение другой.

Методы корреляционно-регрессионного анализа применимы только для таких параметров, которые при изучении физической природы объекта являются взаимосвязанными. Одним из этапов применения этих методов обычно оценивают степень тесноты взаимосвязи значений функции отклика с одной или несколькими независимыми переменными.

Например, в результате выполненных исследований различных систем случайных величин X (х1 , х2 , …, хn) и Y (y1, y2, …, yn)получены некоторые результаты, которые графически представлены на рис. 7.

Расположение точек на графике (поле корреляции) указывает на существование или отсутствие связи между факторными (X) и результативными (Y) признаками.

В-первом случае (рис. 7,а) каждому значению х_i соответствует значение y_i, причем, полученные случайные точки разбросаны на поле координат x, y хаотично и никакой закономерности не просматривается. График наглядно показывает, что величины X и Y не коррелированны (не связаны).

Во-втором случае (рис. 7,б) очевидна ярко выраженная положительная корреляция, так как при возрастании случайной величины X и величина Y также в общем или в среднем возрастает.

Третий случай (рис. 7,в) иллюстрирует практически функциональную линейную зависимость величины Y от величины X, причем, эта зависимость положительная.

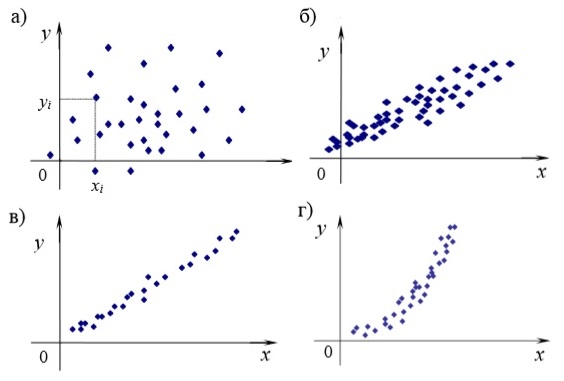
Рис.7. Корреляция случайных величин X и Y:
а – корреляция отсутствует;
б – сильная положительная корреляция;
в – функциональная линейная зависимость;
г – функциональная нелинейная зависимость

Количественная оценка степени взаимной связи (принято говорить о тесноте или силе связи) дается с помощью так называемого коэффициента корреляции.

Если корреляционным анализом подтверждено наличие взаимосвязей между исследуемыми факторами, то на следующем этапе обработки экспериментальныхданных с помощью регрессионного анализа выбирают математическую модель, в наилучшей степени описывающую указанные взаимосвязи.

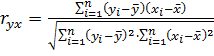(15)

Несмотря на громоздкость формулы (15), она наиболее простая для вычислений.

Значение коэффициента корреляции всегда меньше единицы.

При r = 1.0 величины x и y связаны функциональной связью (в данном случае линейной), т.е. каждому значению x соответствует одно значение y. Если r < 0.5, то линейной связи не существует. Обычно считают тесноту связи удовлетворительной при r ≥ 0.5, хорошей − при r ≥ 0.8…1.0.

Применение корреляционно-регрессионного анализа правомерно и эффективно при соблюдении следующих условий:

1) параметр оптимизации y есть случайная величина с нормальным законом распределения;

2) дисперсия y не зависит от абсолютных значений величины y, остается постоянной или однородной при различных наблюдениях y;

3) значения независимых переменных x₁, x₂, …, x_m измеряются с пренебрежимо малыми ошибками по сравнению с ошибкой в определении y;

4) переменные x₁, x₂, …, x_m линейно независимы;

5) процесс изменения зависимой переменной y является стационарным случайным;

6) экспериментальные данные получены из ряда независимых испытаний, наблюдений и образуют случайную выборку из данной генеральной совокупности.