Первый способ – материал изучен ранее
Второй способ
I. Определение тесноты связей между Y и Хi.
Мастер функций, Статистические,=КОРРЕЛ (массив1, массив2).
<Enter>. На экране: результат вычислений.
II. Определение наиболее значимых из Хi.
IrI<0,3 – слабая связь,
IrI=0,3 – 0,7 – средняя, тесная связь,
IrI>0,7 – существенная связь.
III. Выбор формы уравнения регрессионной зависимости.
IV. Определение коэффициентов уравнения линейной регрессии.
Выделить блок, в котором: строк — всегда 5, столбцов —n+1, где n - число факторов,
Мастер функций, Статистические,=ЛИНЕЙН(интервал значений у, блок значений х; константа; стат).
<Shift>+<Ctri>+<Enter>. На экране: результат вычислений.
Назначить необходимое число десятичных знаков.
Убрать выделение.
| an | an-1 | … | a1 | a0 |
| mn | m n-1 | … | m1 | m0 |
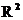 | 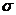 y y | |||
| Fнабл | df | |||
| SSreg | SSresid |
аi ---- коэффициенты уравнения линейной регрессии,
mi— стандартные значения ошибок коэффициентов,
R 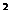 — коэффициент детерминированности,
— коэффициент детерминированности,
m y =Sest-- стандартная ошибка для оценки y,
Fнабл - F-статистика,
df — число степеней свободы,
SSreg — регрессионная сумма квадратов,
SSresid — остаточная сумма квадратов.
V. Оценка достоверности уравнения.
Выбрать ячейку, в которой определяется 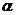 - вероятность недостоверности уравнения.
- вероятность недостоверности уравнения.
Мастер функций, Статистические, FРАСП.
На экране: диалоговое окно FРАСП, в которое ввести следующие величины:
х = Fнабл
степени свободы 1 = число факторов
степени свободы 2 = df
Выбрать ячейку, в которой определяется достоверность уравнения
VI. Оценка достоверности коэффициентов.
Вычислить величины ti = аi/mi,
Выбрать ячейку, в которой определяется 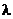 i- вероятность недостоверности коэффициентов аi.
i- вероятность недостоверности коэффициентов аi.
Мастер функций, Статистические, СТЬЮДРАСП.
На экране: диалоговое окно СТЬЮДРАСП, в которое вводятся следующие величины:
x=| ti |,
степени свободы = df
хвосты — 2 (это признак используемого 2-стороннее распределения Стьюдента).
Выбрать ячейку, в которой определяется вероятность достоверности коэффициентов
Третий способ
Для получения решения необходимо воспользоваться функцией Регрессия. Для этого в окне «Анализа данных» необходимо выбрать строку Регрессия. Появляется диалоговое окно, которое заполняется следующим образом:
Входной интервал Y – диапазон (столбец), содержащий данные со значениями зависимой переменной;
Входной интервал Хi – диапазон (столбцы), содержащий данные со значениями независимых переменных.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Уровень надежности – уровень значимости, (например, 0,05).
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист – поставить значок и задать имя нового листа (Отчет - регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора, установите соответствующие флажки в диалоговом окне.
Уравнение регрессии имеет вид: 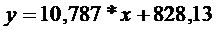
Оценка параметров модели
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множествен. R | 0,847950033 | |||||
| R-квадрат | 0,719019259 | |||||
| Нормированный R-квадрат | 0,683896667 | |||||
| Стандартная ошибка | 67,19447214 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 92431,72 | 92431,72 | 20,4717 | 0,001938 | ||
| Остаток | 36120,78 | 4515,097 | ||||
| Итого | 128552,5 | |||||
| Коэффиц. | Стандарт. ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 828,1268882 | 136,1286 | 6,083416 | 0,000295 | 514,2138 | 1142,04 |
| Переменная X 1 | 10,7867573 | 2,384042 | 4,524567 | 0,001938 | 5,289146 | 16,28437 |
| ВЫВОД ОСТАТКА | ||||||
| Наблюдение | Предсказ. Y | Остатки | ||||
| 1270,383938 | -20,3839 | |||||
| 1410,611782 | -30,6118 | |||||
| 1507,692598 | -82,6926 | |||||
| 1410,611782 | 14,38822 | |||||
| 1345,891239 | 104,1088 | |||||
| 1324,317724 | -24,3177 | |||||
| 1496,905841 | -96,9058 | |||||
| 1486,119084 | 23,88092 | |||||
| 1518,479355 | 56,52064 | |||||
| 1593,986657 | 56,01334 |
Основные параметры регрессионной модели:
1. Множественный R = 0,847950033 (коэффициент корреляции Пирсона).
2. R-квадрат = 0,719019259 (коэффициент детерминации) – показывает долю вариации зависимой переменной, которая объясняется вариацией независимой переменной (значения от 0 до 1). Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям). Величина показывает, какая часть (доля) вариации объясняемой переменной обусловлена вариацией объясняющей переменной.
Нормированный R-квадрат – скорректированный (адаптированный, поправленный(adjusted)) коэффициент детерминации:
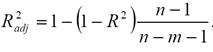
Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать нормированный R-квадрат. В отличие от R-квадрат, скорректированный коэффициент может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
3. Стандартная ошибка = 67,19
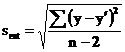 |
Значение 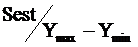 не должно превышать 30%.
не должно превышать 30%.
df – degrees of freedom – число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант.
4. F – критерий Фишера, значимость F < 0,05.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
SS – Сумма квадратов отклонений значений признака Y.
MS – Дисперсия на одну степень свободы.
F – Наблюдаемое (эмпирическое) значение статистики F, по которой проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
5. t – статистика (коэффициент Стьюдента) – значение должно быть > 2; р – значение < 0,05; доверительный интервал не должен включать 0. Эти три показателя между собой взаимосвязаны и интерепретируются одинаково: переменная Х оказывает значимое влияние на переменную Y.
6. Остатки (влияние случайных факторов) – коэффициент автокорреляции для остатков должен стремиться к нулю. Рассчитывается как коэффициент корреляции для двух наборов данных их одного столбца: первый – значения с 1 по 9 (предпоследний), второй – значения с 2 по 10 (последний).
Проверка модели на возможность ее практического применения производится по критериям точности, надежности и адекватности. Все параметры должны выполняться одновременно. Несоответствие одному из критериев означает отсутствие модели как таковой.
Точность оценивается по значениям коэффициента корреляции r, коэффициента детерминации r2 и стандартной ошибки m.
| Критерий | Критическое значение | Расчетное значение | Вывод о точности модели |
| r | > 0,7 | 0,847 | + |
| r2 | > 0,5 | 0,719 | + |
| m% | < 30% | 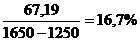 | + |
Надежность модели оценивается по значениям F – для модели в целом и значениям t, p и доверительного интервала – для независимой переменной Х.
| Критерий | Критическое значение | Расчетное значение | Вывод о надежности модели | |
| для модели | F | F > Fтабличн | 20,47 | + |
| Значимость F | < 0,05 | 0,0018 | + | |
| Для независимой переменной Х | t | t > 2 | 4,524 | + |
| p | p < 0,05 | 0,0019 | + | |
| доверительный интервал | 0 отсутствует | 5,289 – 16,283 | + |
Адекватность модели оценивается по коэффициенту автокорреляции.
| Критерий | Критическое значение | Расчетное значение | Вывод о точности модели |
| автокорреляция | < 0,3 | 0,164 | + |
| ВЫВОД ОСТАТКА | ||||
| Наблюдение | Предсказанное Y | Остатки | Автокорреляция | |
| 1270,383938 | -20,3839 | 0,164647 | ||
| 1410,611782 | -30,6118 | |||
| 1507,692598 | -82,6926 | |||
| 1410,611782 | 14,38822 | |||
| 1345,891239 | 104,1088 | |||
| 1324,317724 | -24,3177 | |||
| 1496,905841 | -96,9058 | |||
| 1486,119084 | 23,88092 | |||
| 1518,479355 | 56,52064 | |||
| 1593,986657 | 56,01334 |
Вывод:
Уравнение 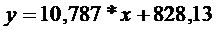 , описывающее зависимость двух переменных отвечает требованиям точности, надежности и адекватности и может быть использовано для прогнозирования результатов.
, описывающее зависимость двух переменных отвечает требованиям точности, надежности и адекватности и может быть использовано для прогнозирования результатов.
Таким образом, при расходах на рекламу в размере 50 и 80 денежных единиц, прогнозируется объем продаж на уровне 1367 и 1690 соответственно.
Задача. Составить многофакторную корреляционную модель среднечасовой выработки по данным таблицы, где
Y - среднечасовая выработка участка цеха, д.е.,
Х1 -- фондовооруженность труда, тыс. д.е.,
Х2 – процент рабочих, имеющих высшую квалификацию,
Х3 – средний срок службы оборудования, лет,
Х4 – процент прогрессивного оборудования.
| № | Y | X1 | X2 | X3 | X4 |
Практическая работа 2.
Непараметрические методы

 0
0
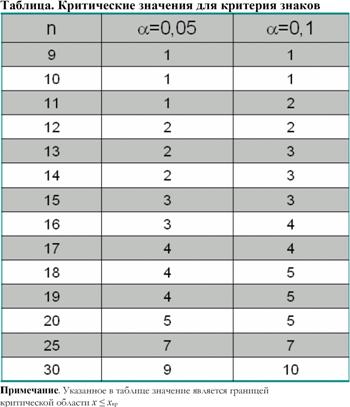
Задача 1. Из 50 опрошенных студентов 29 предпочитали бы жить в общежитиях в одноместной комнате. При α=0,05 проверьте гипотезу о том, что более 50% студентов предпочитают жить в общежитиях в одиночку. Задача 2. . Было проведено исследование, чтобы выяснить, повлияют ли новые диетические медикаменты на женщин, желающих сбросить вес. Вес 8 пациенток был измерен до лечения и через 6 недель ежедневного применения лечения. Данные приведены ниже. Можно ли сделать вывод, что лечение повлияло (увеличило или уменьшило) на вес этих женщин?

Задача 3. Двум группам рабочих дали вопросники, чтобы установить степень их удовлетворенности работой. Задавалась шкала диапазоном от 0 до 100. Группы делились по стажу: те, кто работал более 5 лет, и те, кто работал менее 5 лет. Данные приведены ниже. Проверьте заявление о том, что между удовлетворенностью работой двух групп нет разницы.

