III. Автокорреляция уровней временного ряда и выявление его структуры

Представлены поквартальные данные о валовом объеме продаж

(млн.шт.) за последние четыре года:

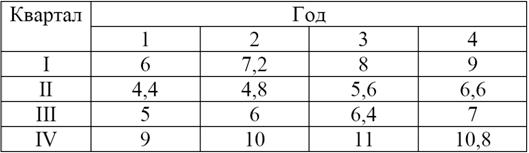
Введем исходные данные

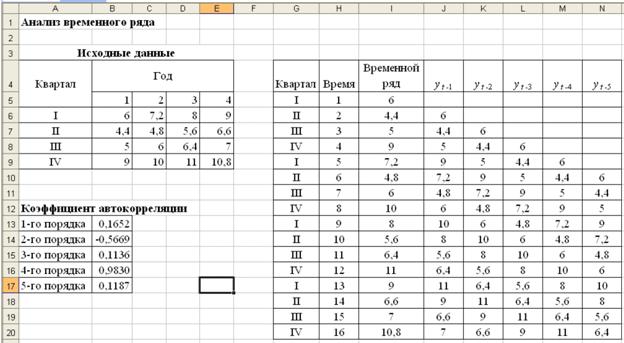
Найдем коэффициенты автокорреляции с помощью следующих формул:

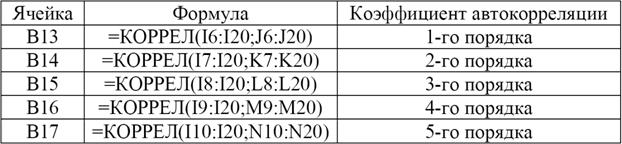
Выделим диапазон А13:В17 и, выбрав в Мастере диаграммтип –Гистограмма, построим коррелограмму

Графики

Графики дают возможность оценить состояние процесса на данный момент, а также спрогнозировать более отдалённый результат по тенденциям процесса, которые можно обнаружить на графиках (конечно, надо учитывать, что такие прогнозы могут быть во многих случаях достаточно условными). При отражении на графике изменения данных во времени график ещё называют временным рядом.

Обычно используют следующие виды графиков:

1.Выраженный ломаной линией

2.Столбчатый

3.Круговой

График, выраженный ломаной линией, применяется, когда необходимо самым простым способом представить изменение данных за определённый период времени, например, изменение размера ежегодной выручки от продажи изделий, объёма производства или доли дефектных изделий.

Пример 1. Отобразить при помощи линейного графика характер изменения размера ежегодной выручки от продажи изделий (табл. 1.), а также спрогнозировать тенденцию изменения выручки в ближайшие два года.

Таблица 1

Год
Выручка, тыс. у.е.

Создаём новую книгу Excel. Вводим заголовок работы, а также исходные данные в соответствии с табл. 1, после чего строим линейный график. На первом шаге мастера диаграмм выбираем точечную диаграмму, на которой значения соединены отрезками. На втором шаге вводим диапазон данных. На третьем шаге вводим заголовки диаграммы и осей, основные линии сетки по осям, удаляем легенду. Полученную диаграмму редактируем при помощи контекстных меню (Рис. 1).

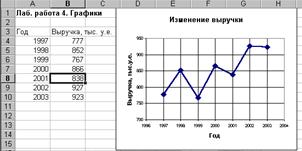Рис 1. Построение линейного графика

Характер изменения выручки, а также прогноз даёт линия тренда, построить которую можно, открыв контекстное меню на ломаной линии и выбрав команду Добавить линию тренда. В открывшемся диалоговом окне на вкладке Тип показаны возможные типы линии тренда. Чтобы выбрать тип линии, наилучшим образом аппроксимирующий данные, можно поступить следующим образом: поместить на диаграмме линии тренда всех приемлемых типов (т.е. линейную, логарифмическую, полиномиальную второй степени, степенную и экспоненциальную), задав для каждой линии на вкладке Параметры прогноз вперёд на две единицы и размещение на диаграмме величины достоверности аппроксимации. При этом после построения очередной линии величину достоверности аппроксимации R² (например, для линейного типа R² = 0,6495) указателем мыши целесообразно установить на свободное место диаграммы в ряд с остальными (Рис 2).

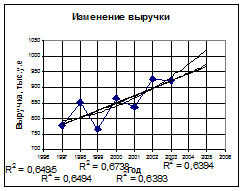Рис 2. Выбор типа линии тренда по величине достоверности аппроксимации.

Наибольшую достоверность аппроксимации даёт полиномиальная линия со степенью два (R² = 0,6738), которую и выбираем в качестве линии тренда. Для этого удаляем с диаграммы все линии тренда, после чего восстанавливаем полиномиальную линию второй степени (Рис. 3).

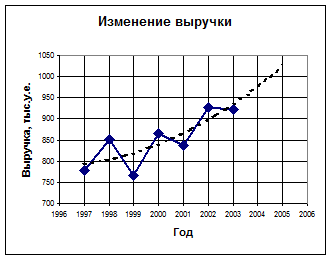Рис 3. График с аппроксимирующей линией в примере 4.1.

По аппроксимирующей линии можно предположить, что выручка в ближайшие два года будет иметь тенденцию к возрастанию.

Столбчатый график представляет количественную зависимость, выраженную высотой столбика. Например, зависимость себестоимости от вида изделия, сумма потерь в результате брака в зависимости от процесса и т.д. Обычно столбики показывают на графике в порядке убывания высоты справа налево. Если в числе факторов имеется группа «Прочие», то соответствующий столбик на графике показывают крайним справа.

Пример 2.На рисунке 4 показаны в виде столбчатого графика результаты исследования стимулов покупки изделия.

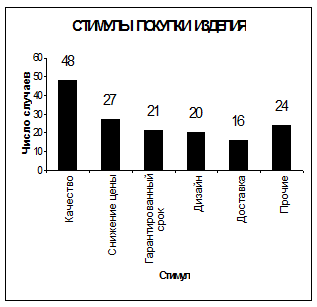Рис 4. Стимулы покупки изделия в примере 3.2.

Круговым графиком выражают соотношение составляющих целого параметра, например, соотношение сумм выручки от продажи отдельно по видам деталей и полной суммы выручки; соотношение элементов, составляющих себестоимость изделия, и т.д.

Пример 3.На рис. 5 показано в виде кругового графика соотношение отказов комбайна по узлам и агрегатам (Исходные данные для построения кругового графика приведены в табл. 2).

Таблица 2

№ п/п	Вид отказа	Количество отказов
	Жатвенная часть
	Гидрооборудование
	Мотор
	Молотилка
	Ремни
	Электрооборудование
	Гидротрансмиссия
	Мост
	Прочие

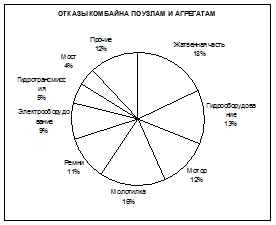
Рис 5. Соотношение отказов комбайна по узлам и агрегатам в

Задание

Выполнить расчёты и построения в соответствии с примерами 1, 2, 3.

Лабораторная работа № 4

Гистограммы

Целью лабораторной работы является приобретение навыков группирования и обработки первичной статистической информации в среде Excel.

Основные понятия.

1. Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по определенному признаку.

2. Ранжированный ряд данных – это упорядоченная совокупность исходных данных в убывающем или возрастающем порядке.

3. Варианты – это числовые значения количественного признака в вариационном ряду распределения.

4. Частоты – это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот называется объемом совокупности и определяется числом элементов всей совокупности.

5. Частости – это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100%. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.

6. Абсолютная плотность распределения – это частота, приходящаяся на единицу для интервала.

7. Относительная плотность распределения – это частость, приходящаяся на единицу длины интервала.

8. Полигоном частот называют ломанную, отрезки которой соединяют некоторые точки. Для построения полигона частот на оси абсцисс откладывают варианты, а на оси ординат - соответствующие им частоты. Точки соединяют отрезками прямых и получают полигон частот.

9. Полигоном относительных частот называют ломанную, отрезки которой соединяют точки. Для построения полигона относительных частот на оси абсцисс откладывают варианты, а на оси ординат - соответствующие им частости. Точки соединяют отрезками прямых и получают полигон относительных частот.

10. Кумулята – ломаная кривая, строящаяся на основе прямоугольной системы координат, когда по оси абсцисс откладываются значения признака, а по оси ординат – накопленные частоты.

11. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты соответствуют частоте повторения варианты (значению количественного признака). В ряде случаев высота может соответствовать абсолютной плотности распределения.

12. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны величине частости. В ряде случаев высота может соответствовать относительной плотности распределения.

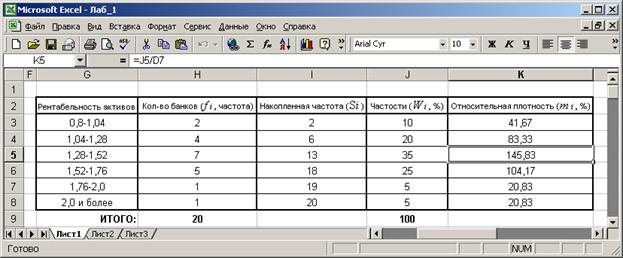
Задание. Проранжировать первичный ряд данных, определить частоты и частости нового ряда, найти абсолютную и относительные плотности распределения, перегруппировать данные для сопоставления и анализа двух рядов, графически изобразить кривые распределения рядов, представить данные в виде полигона частот, гистограмм, кумулятивных кривых по известным накопленным частотам.

Условие. Имеются разрозненные данные по рентабельности активов банков с доходами от 50 до 100 млн. долл.:

№	Рентабельность активов, %
	0,86
	1,88
	1,22
	0,63
	1,64
	1,01
	1,43
	1,33
	1,21
	1,69
	0,65
	1,54
	0,89
	1,61
	1,37
	1,51
	1,65
	1,51
	0,65
	1,11
	1,56
	0,74
	1,05
	1,78
	1,37
	1,64
	1,25
	1,35
	1,74

Этапы выполнение задания.

1. В программной среде Excel заполняется столбец исходных данных.

2. Выполняется сортировка первичного ряда в порядке возрастания. В результате получен интервальный ранжированный ряд.

3. Определяются частоты и частости, относительная плотность распределения.

4. Проводится перегруппировка данные исследуемого интервального вариационного ряда для сопоставления и анализа двух рядов.

5. Формируется полигон частот.

6. Строится гистограмма

7. Строится кумулятивная кривая накопленных частот.

8. Делаются выводы.

Пример решения задачи.

Условие. Имеются разрозненные данные по рентабельности активов банков с доходами от 50 до 100 млн. долл.:

1,51; 0,85; 1,37; 1,62; 0,80; 2,0; 1,49; 1,58; 1,75; 1,24; 1,28; 1,04; 1,98; 1,15; 1,66; 1,33; 1,73; 1,13; 1,36; 1,28.

В программной среде Excel заполняется столбец исходных данных.

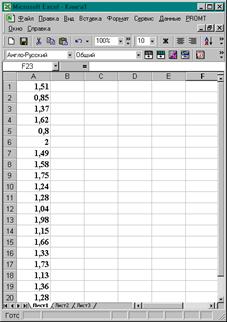
1. Выполняется сортировка столбца А - первичного ряда в порядке возрастания. В результате получен новый интервальный ранжированный ряд.

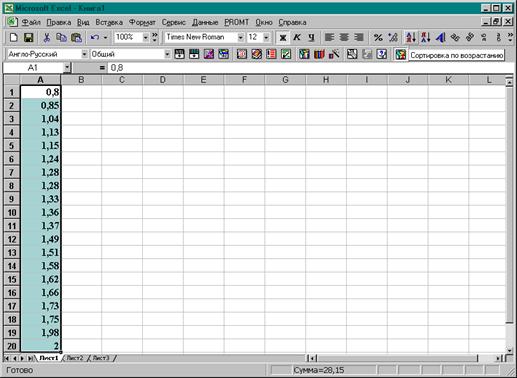
2. Определяются частоты и частости нового ряда. Для этого используется данные об объеме совокупности исследуемых банков N = 20 . Дискретный вариационный ряд разбивается на интервалы, число которых подсчитывается по формуле Стержесса

k = 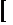1 + 3,322 lg N ,

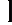в которой квадратные скобки означают округление числа 5,32 , тогда k = 5. Длина частичного интервала определяется по формуле

.

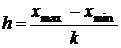x_max = 2,0 , x_min = 0,8 , h = 0,24. Тогда границы интервалов будут такими:

x0= xmin =0,8 ;

x1= xmin + h = 1,04 ;

x2= xmin + 2h = 1,28 ;

x3= xmin + 3h = 1,52 ;

x4= xmin + 4h = 1,76 ;

x5= xmin + 5h = 2 .

Подсчитывается количество банков принадлежащих каждому из интервалов. Вычисляется накопленная частота и процентное отношение частоты к общему объему всей совокупности N = 20 или частость. Для сопоставления полученных данных интервального вариационного ряда с данными другого вариационного ряда с неравными интервалами необходимо рассчитать относительную плотность распределения

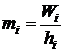, h_i = h

Необходимо перегруппировать данные исследуемого интервального вариационного ряда для сопоставления и анализа двух рядов.

Таблица 2.

Группы банков с доходами от 100 до 300 млн. долл.	Группы банков с доходами от 50 до 100 млн. долл.
Рентабельность активов	Количество банков в % (частости)	Количество банков в % (частости)
0,6 – 0,8		-
0,8 – 1,0		8,33 =0,2m1
1,0 – 1,1		6,67
1,1 – 1,2		8,33
1,2 – 1,4		24,17
1,4 – 1,8		43,33 =(1,52-1,4)m3+0,24 m4+(1,8-1,76) m5
1,8 – 2,0		4,17
2,0 и более	-	5,00
ИТОГО:		100,00

Расчетная схема представлена ниже.

Необходимо вычислить новые величины интервалов, используя заготовленный рисунок :

h₀₁ = y₀ – x₀ ,

h₁₁ = x₁ – y₀ ,

h₁₂ = y₁ – x₁ ,

h₂₁ = x₂ – y₁ ,

h₂₂ = x₃ – x₂ ,

h₂₃ = x₄ – x₃ ,

h₂₄ = y₂ – x₄ ,

h₃₁ = x₅ – y₂ ,

h₃₂ = x₆ – x₅ ,

…

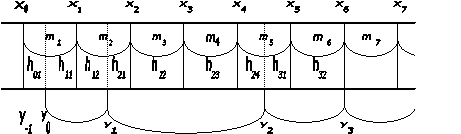Здесь – узловые точки x_i рентабельности активов, отстоящие друг от друга на один и тот же равный шаг h , y_i – узловые точки интервального ряда рис. 1 (i = ).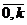

На промежутках [y_-1, y₀] U [y₀, y₁] U [y₁, y₂] U [y₂, y₃] частости W_i перераспределяются следующим образом:

[y_-1, y₀] ¾ W₀ = h₀₁m₁ ,

[y₀, y₁] ¾ W₁ = h₁₁m₁ + h₁₂m₂ ,

[y₁, y₂] ¾ W₂ = h₂₁m₂ + h₂₂m₃+ h₂₃m₄+ h₂₄m₅ ,

[y₂, y₃] ¾ W₃ = h₃₁m₅ + h₃₂m₆ ,

Полученными новыми значениями W_i заполняется третий столбец таблицы 2.

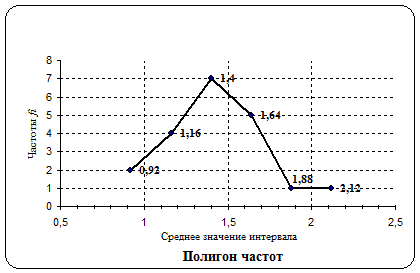
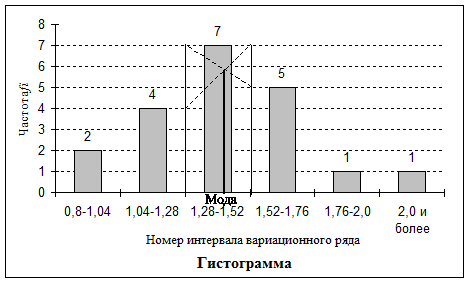
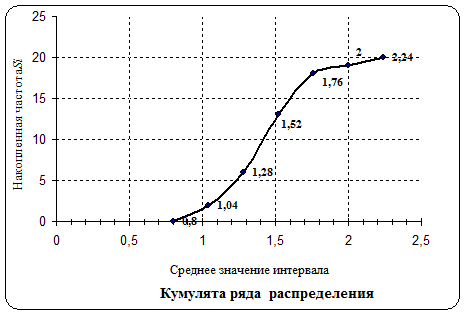
Рис. 7.

Гистограмма – это серия столбиков одинаковой ширины, но разной высоты, показывающая рассеяние и распределение данных. Ширина столбика – это интервал в диапазоне наблюдений, высота – количество данных, приходящихся на тот или иной интервал, т.е. частость. По существу, гистограмма отображает распределение исследуемого показателя. Гистограмма позволяет оценить характер рассеивания показателя и разобраться в том, на чём следует сосредоточить усилия по улучшению.

Характерные типы гистограмм показаны на рис.

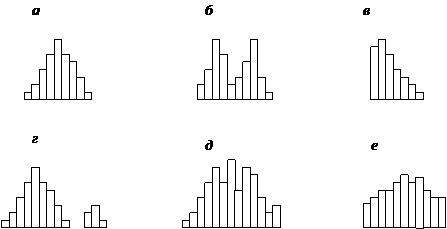Рис 1. Характерные типы гистограмм

На рис. 1,а показан обычный тип гистограммы с двусторонней симметрией, что указывает на стабильность процесса.

На рис 1,б в распределении имеется два пика (двугорбая гистограмма). Такая гистограмма получается при объединении двух распределений, например, в случае двух видов сырья, изменения настройки процесса или объединения в одну партию изделий, обработанных на двух разных станках. Требуется расслоение продукции.

На рис. 1,в показана гистограмма с обрывом. Такое распределение получается, когда невозможно получить значение ниже (или выше) некоторой величины. Подобное распределение имеет место также, когда из партии исключены все изделия с показателем ниже (и/или выше) нормы, т.е. изначально это была партия с большим количеством дефектных изделий. Такое же распределение получается, когда измерительные приборы были неисправны.

На рис. 1,г показана гистограмма с островком. Получается при ошибках в измерениях, или когда некоторое количество дефектных изделий перемешано с доброкачественными.

На рис. 1,д показана гистограмма с прогалами («гребёнка»). Получается, когда ширина интервала не кратна единице измерения или при ошибках оператора.

На рис. 1,е показана гистограмма в форме плато. Получается, когда объединяются несколько распределений при небольшой разнице средних значений. В этом случае требуется расслоение.

Пример 1. Выявить характер рассеяния показателя качества изделий из металлического материала.

Для определения характера рассеяния показателя строим гистограмму.

Порядок построения гистограммы:

1. Намечаем исследуемый показатель качества. В данном случае это коэффициент деформации материала.

2. Проводим измерения. Должно быть не менее 30…50 данных, оптимально – около 100.

Результаты измерений коэффициента деформации представлены в табл. 6.1.

Результаты измерений вводим в электронную таблицу. В ячейку А1 вводим заголовок работы. Начиная с ячейки А3 вводим в столбец порядковые номера измерений с 1 по 100. В ячейки В3:В102 вводим значения коэффициента деформации из табл. 1.

1.Вводим единицу измерений. Единица измерений равна точности, с которой проводились измерения, в данном случае 0,1. Вводим единицу измерений в ячейку Е2.

Таблица 1.

0,9	1,5	0,9	1,1	1,0	0,9	1,1	1,1	1,2	1,0
0,6	0,1	0,7	0,8	0,7	0,8	0,5	0,8	1,2	0,6
0,5	0,8	0,3	0,4	0,5	1,0	1,1	0,6	1,2	0,4
0,6	0,7	0,5	0,2	0,3	0,5	0,4	1,0	0,5	0,8
0,7	0,8	0,3	0,4	0,6	0,7	1,1	0,7	1,2	0,8
0,8	1,0	0,6	1,0	0,7	0,6	0,3	1,2	1,4	1,0
1,0	0,9	1,0	1,2	1,3	0,9	1,3	1,2	1,4	1,0
1,4	1,4	0,9	1,1	0,9	1,4	0,9	1,8	0,9	1,4
1,1	1,4	1,4	1,4	0,9	1,1	1,4	1,1	1,3	1,1
1,5	1,6	1,6	1,5	1,6	1,5	1,6	1,7	1,8	1,5

4. Находим минимальное и максимальное значения выборки. Минимальное и максимальное значения выборки находим с помощью статистических функций МИН и МАКС соответственно в ячейках Е3 и Е4. При этом интервал для этих функций указываем от ячейки В3 до ячейки В102.

5. Находим размах выборки в ячейке Е5 как разность между максимальным и минимальным значениями выборки.

6. Определяем предварительное количество интервалов К_предв как квадратный корень из объёма выборки N. Количество интервалов находим в ячейке Е6. Поскольку количество интервалов должно быть целым числом, т.е. полученный квадратный корень следует округлить до целого значения, то сначала в ячейку Е6 вводим математическую функцию ОКРУГЛ. В строке Количество_цифрэтой функции указываем 0, т.к. необходимо округление до целого числа. Затем переводим курсор в строку Число и в качестве аргумента функции ОКРУГЛ встраиваем функцию КОРЕНЬ. Для этого в строке формул открываем список функций, выбираем Другие функции… и открываем математическую функцию КОРЕНЬ. В качестве аргумента функции КОРЕНЬ опять при помощи списка в строке формул выбираем статистическую функцию СЧЁТ, в качестве аргумента которой вводим диапазон ячеек от В3 до В102. Поскольку функция СЧЁТ подсчитывает количество чисел в указанном диапазоне, т.е. в данном случае объём выборки, то будет получено значение 100. Затем функция КОРЕНЬ пересчитает это значение в 10, а функция ОКРУГЛ округлит его до целых, т.е. до 10. В целом формула в ячейке Е6 будет выглядеть примерно так: =ОКРУГЛ(КОРЕНЬ(СЧЁТ(B3:B102));0)

7. Определяем ширину интервала в ячейке Е7 по формуле h = R/K_предв с округлением до единицы измерения, т.е. в нашем случае до десятых долей. Формула в ячейке Е7 будет выглядеть так: =ОКРУГЛ(E5/E6;1).

8. Вводим номера интервалов. Для этого в ячейку D9 вводим заголовок столбца № инт. Начиная с ячейки D10 вводим номера интервалов с 1 примерно до 25.

9. Рассчитываем границы и середины интервалов. В ячейке Е10 рассчитываем нижнюю границу первого интервала по формуле

X_min – ед.изм./2

Для этого в ячейку Е10 вводим формулу =E3-E2/2 и получаем значение нижней границы первого интервала 0,05.

В ячейке Е11 рассчитываем нижнюю границу второго интервала, прибавляя к нижней границе первого интервала значение шага. Формула в ячейке Е11 будет выглядеть =E10+E7. После указания необходимой абсолютной адресации копирует эту формулу в диапазон Е12:Е34.

В ячейке F10 рассчитываем верхнюю границу первого интервала, прибавляя к его нижней границе значение шага. После указания необходимой абсолютной1 адресации полученную формулу копируем в диапазон F11:F34.

В ячейке G10 рассчитываем среднее значение первого интервала, например, по статистической формуле СРЗНАЧ. Полученную формулу копируем в диапазон G11:G34.

Поскольку уже в десятом интервале нижняя граница равна 1,85. что больше X_max, то необходимое количество интервалов равно 9. Поэтому содержимое ячеек диапазона D19:F34 следует очистить.

10. Подсчитываем частоты появления результатов измерений в интервалах. В ячейке Н10 рассчитываем частоту для первого интервала при помощи статистической функции СЧЁТЕСЛИ. Функция СЧЁТЕСЛИ подсчитывает количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. Следует подсчитать, сколько раз в диапазоне B3:B102 встречаются ячейки, значения которых находятся в границах первого интервала, т.е. больше 0,05, но меньше 0,25. Таким образом, надо подсчитать ячейки, значения которых удовлетворяют двойному условию. Однако функция СЧЁТЕСЛИ использует только одинарное условие. Поэтому в формуле, записываемой в ячейке Н10, функцию СЧЁТЕСЛИ используем дважды. Сначала в функции СЧЁТЕСЛИ вводим диапазон В3:В102 и условие “>0,05”. (к сожалению, нельзя указать условие ‘>E10”, ссылаясь на значение нижней границы интервала, поскольку функция СЧЁТЕСЛИ использует условие критерий в форме числа, выражения или текста, но не в форме ссылки на ячейку). Затем переводим курсор в строку формул, ставим знак минус, вновь вводим функцию СЧЁТЕСЛИ, указываем в ней диапазон В3:В102 и условие “>0,25”. В результате получаем расчётную формулу =СЧЁТЕСЛИ(B3:B102;">0,05")-СЧЁТЕСЛИ(B3:B102;">0,25"), по которой рассчитывается частота для первого интервала. После указания абсолютной адресации для интервалов копируем эту формулу в диапазон Н11:Н18. Поскольку в копируемой формуле границы интервалов были указаны численными значениями, то в формулах ячеек диапазона Н11:Н18 следует исправить численные значения границ на соответствующие тому или иному диапазону. Например. в ячейке Н11 формула будет выглядеть так: =СЧЁТЕСЛИ($B$3:$B$102;">0,25")-СЧЁТЕСЛИ($B$3:$B$102;">0,45").

Результаты расчётов показаны на рис. 1.

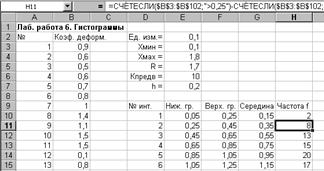Рис. 1. Расчёт данных для построения гистограммы в примере 6.1.

11. Строим гистограмму распределения. Открываем мастер диаграмм, выбираем тип Гистограмма и вид Обычная гистограмма отображает значения различных категорий. На втором шаге на вкладке Диапазон данных указываем диапазон Н10:Н18. На вкладке Рядв строке Подписи по Х указываем диапазон G10:G18 (возможно указание диапазона Е10:F18). На третьем шаге вводим заголовки по осям, а также убираем легенду и линии сетки. После создания диаграммы редактируем её, используя контекстное меню. В частности, открыв контекстное меню на одном из столбцов диаграммы, выбираем команду Формат рядов данных…, вкладку Параметры, и устанавливаем ширину зазора 0.

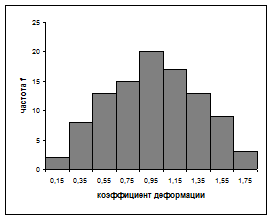
Готовая гистограмма показана на рис. 6.2,а.

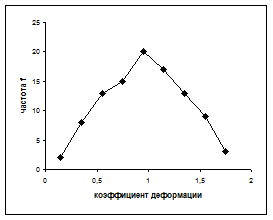
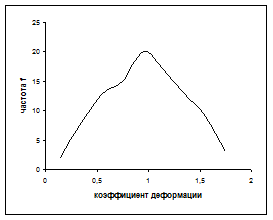
Возможно представление гистограммы в виде непрерывной кривой или ломаной линии. Для этого надо в области гистограммы открыть контекстное меню, выбрать команду Тип диаграммы…, выбрать диаграмму Точечная и соответствующий её вид. (Рис. 2,б,в).

а б

в

Рис 2. Гистограмма в виде столбиковой диаграммы (а), ломаной линии (б) и непрерывной кривой (в).

Полученная гистограмма близка к обычной гистограмме с двусторонней симметрией, что указывает на стабильность процесса.

Задание

1.Выполнить расчёты и построения в соответствии с примером 6,1.

2.Построить гистограмму по результатам измерения длины деталей, мм (табл. 2). Какие меры необходимы для стабилизации технологического процесса?

Таблица 2.

10,6	10,4	11,1	10,5	10,7	10,2	10,6	10,7	10,4	10,7
10,4	10,5	10,9	10,6	10,7	10,6	10,7	10,5	10,3	10,7
10,3	10,7	10,6	10,7	10,5	10,9	10,6	10,9	10,4	10,8
10,5	10,8	10,7	10,3	10,8	10,5	10,4	10,5	10,7	10,6
10,4	10,3	10,6	10,7	10,5	10,9	10,6	11,0	10,6	10,8
10,5	10,8	10,4	10,8	10,9	10,5	10,9	10,6	10,9	10,4
10,4	10,6	10,8	10,4	10,5	10,7	10,4	10,7	10,6	10,7
10,5	10,8	10,5	10,3	11,0	10,6	10,3	10,5	10,8	10,6
10,6	10,5	10,4	10,7	10,6	10,8	10,7	10,3	10,6	11,0
10,7	11,1	10,5	10,6	10,5	10,5	10,4	10,8	10,4	10,6
11,0	10,7	10,3	10,8	10,7	10,2	10,8	10,6	10,8	10,8
10,5	10,7	10,8	10,4	10,6	10,5	10,7	11,1	10,5	10,6
10,7	10,6	10,7	10,3	10,7	10,3	10,6	10,8	10,1	10,7
11,0	10,5	10,5	10,1	10,3	11,0	11,2	10,6	11,1	10,2

Диаграмма Парето

Диаграмма Парето строится в виде столбчатого графика и показывает в убывающем порядке относительное влияние каждой причины на общую проблему. Кроме того, на диаграмме обычно приводят кумулятивную кривую накопленного процента причин.

Диаграмма Парето позволяет анализировать проблемы из любой сферы деятельности предприятия, в том числе в сфере управления качеством. Причины изменений качества делятся на две группы: немногочисленные существенно важные и многочисленные несущественные. Устраняя причины первой группы, можно устранить почти все потери, вызванные снижением качества.

Диаграмму Парето целесообразно применять вместе с причинно-следственной диаграммой.

При использовании диаграммы Парето обычно сначала строят диаграмму по результатам деятельности для выявления главной из существующих проблем. Затем строят диаграмму по причинами для выявления главных причин этой проблемы и её решения и т.д. После проведения корректирующих мероприятий диаграмму Парето можно вновь построить и проверить эффективность проведённых улучшений.

При использовании диаграммы Парето для контроля важнейших факторов распространён АВС-анализ. Например, если на складе находится большое число деталей, проводить контроль всех деталей без всякого различия неэффективно. Но если разделить детали на группы по их стоимости, то на долю группы наиболее дорогих деталей (группа А), составляющих 20-30% от общего числа деталей, придётся 70-80% от общей стоимости всех деталей. На долю группы самых дешёвых деталей (группа С), составляющей 40-50% от всего количества деталей, придётся всего 5-10% от общей стоимости. Стоимость промежуточной группы (группа В) составляет 20-30% от общей стоимости. Контроль деталей на складе будет эффективным, если контроль деталей группы А будет самым жёстким, а контроль деталей группы С – упрощённым.

Рекомендуется составлять несколько вспомогательных диаграмм, входящих в состав группы А, с тем чтобы, последовательно анализируя их, в конечном итоге составить отдельную диаграмму Парето для конкретных явлений недоброкачественности.

Пример. Исследовать проблему появления брака при выпуске деталей.

С учётом того, что потери от брака одной детали каждого вида примерно одинаковы, в качестве единицы измерения выбираем число дефектных деталей каждого вида. После заполнения контрольных листков получаем данные, представленные в табл.

Таблица

№ детали							Прочие
Число дефектных деталей

По полученным данным разрабатываем таблицу для проверок данных. Создаём новую книгу Excel. В ячейке А1 вводим заголовок работы. В ячейки А3:Е3 вводим заголовки: № детали, Число дефектных деталей, Накопленная сумма деталей, Процент деталей, Накопленный процент. Для компактного размещения заголовков выделяем третью строку и используем команду Формат4Ячейки..., вкладку Выравнивание, режим выравнивания по вертикали По центру, режим отображения Переносить по словам.

В ячейки А4:В10 вводим данные из таблицы . В ячейку А11 вводим заголовок Итого. В ячейке В11 рассчитываем суммарное число дефектных деталей при помощи математической формулы СУММ.

Для расчёта накопленной суммы деталей в ячейку С4 вводим значение 255, т.е. число дефектных деталей 1. В ячейке С5 суммируем число дефектных деталей 1 и 2, т.е. вводим формулу =C4+B5. Для расчёта накопленной суммы деталей в остальных ячейках копируем формулу из ячейки С5 в диапазон С6:С10.

Для расчёта процента деталей следует делить число дефектных деталей каждого вида на общее число дефектных деталей и умножать на 100. Таким образом, в ячейку D4 вводим формулу =B4/B11*100. После указания необходимой абсолютной адресации копируем эту формулу в диапазон D5:D10. В ячейке D11 рассчитываем суммарный процент, который должен составить 100%.

Для расчёта накопленного процента деталей в ячейку Е4 значение (только значение, а не формулу) из ячейки D4. Для этого используем команды Правка4Копироватьи Правка4Специальная вставка... . В ячейке Е5 суммируем процент дефектных деталей 1 и 2, т.е. вводим формулу =E4+D5. Для расчёта накопленного процента в остальных ячейках копируем формулу из ячейки Е5 в диапазон Е6:Е10.

По таблице для проверок данных строим диаграмму Парето. Для этого открываем в мастере диаграмм вкладку Нестандартные, выбираем диаграмму типа График/гистограмма 2. На втором шаге указываем диапазон данных А4:В10; Е4:E10. На третьем шаге вводим заголовки и убираем легенду.

После создания диаграммы мастером диаграмм редактируем её при помощи контекстных меню. В частности, максимальное значение шкалы Число дефектных деталей указываем 506, а минимальное 0. Максимальное значение шкалы Накопленный процентуказываем 100. Открываем контекстное меню на одном из столбцов, выбираем команду Формат рядов данных..., вкладку Параметры, и устанавливаем ширину зазора 0.

Результаты расчётов и построений показаны на рис.

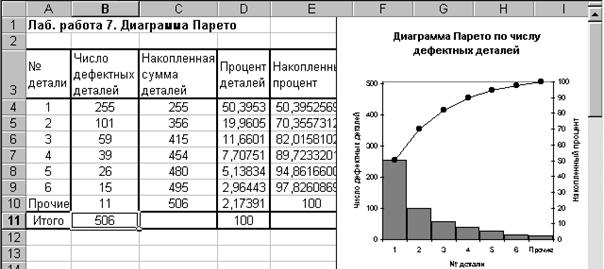Рис. Построение диаграммы Парето по числу дефектных деталей.

Как видно из диаграммы, к группе А можно отнести детали 1 и 2 (70% от брака), к группе В – детали 3,4,5, к группе С – детали 6 и прочие.

Для выяснения наиболее важных дефектов целесообразно построить диаграммы Парето по явления дефектности в деталях 1 и 2.

Рассмотрим построение такой диаграммы для детали 1. В качестве единицы измерения выбираем сумму потерь от брака, млн. руб. После исследования явлений дефектности получили данные, представленные в табл.

Таблица

Дефект	Сумма потерь, млн. руб.
Шаг резьбы завышен	1,5
На режущей кромке резца налипы	6,9
Зависание	1,9
Пропуск операции	0,4
Осталась чернота	0,9
Скос кромки увеличен	0,6
Наружный диаметр занижен	8,3
Прочие	0,2

Диаграмма Парето, построенная по этим данным, показана на рис.7.2.

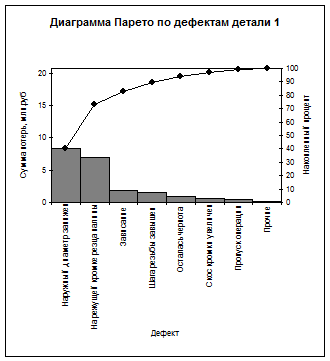Рис. Диаграмма Парето по дефектам детали 1.

Как видно из диаграммы, к группе А можно отнести занижение наружного диаметра и налипы на режущей кромке резца (73% от суммы потерь), к группе В – зависание, завышение шага резьбы, остаточную черноту, к группе С – увеличение скоса кромки, пропуск операции и прочие.

Для выяснения наиболее важных причин потерь целесообразно построить диаграммы Парето по причинам занижения наружного диаметра и налипов на режущей кромке резца.

При построении такой диаграммы для причин занижения наружного диаметра после заполнения контрольных листков получили данные, представленные в табл.

Таблица

Причина	Число дефектов
Смещение копира
Неопытность оператора
Неточность рабочего инструмента
Устаревший чертёж
Ошибки в управлении станком
Неточность станка
Прочие

По этим данным необходимо построить диаграмму Парето, выявить причины занижения наружного диаметра группы А и провести по ним корректирующие мероприятия. После этого можно вновь построить диаграмму Парето для изменившихся условий, чтобы проверить эффективность улучшений.

Задание

Выполнить расчёты и построения в соответствии с примером, включая, диаграмму Парето по причинам занижения наружного диаметра.

Практическая работа №1