Б. Точки экстремума функции.

Точками экстремума могут быть только те точки, в которых производная или равна нулю или не существует.

У исследуемой функции таких точек пять: х=-1, х=1, х=0, 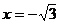, 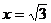. В точках х=-1, х=1 функция не определена, а значит, они не могут быть точками экстремума.

При переходе через точку х=0 знак производной не изменяется, а значит, она не является точкой экстремума.

При переходе через точку 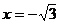производная меняет свой знак с минуса на плюс и, следовательно, точка 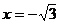является точкой минимума. При переходе через точку 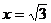производная меняет свой знак с плюса на минус и, следовательно, точка 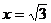является точкой максимума.

Вычислим значения функции в точках экстремума:

точка 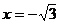является точкой минимума, .

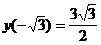точка 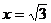является точкой максимума, .

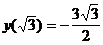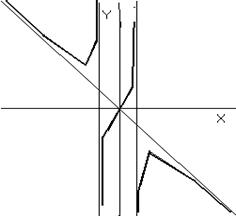
С учетом проведенного исследования уже может быть построен схематичный график.

7. Выпуклость, вогнутость, точки перегиба графика функции.

Напомним некоторые понятия.

Функция называется выпуклой (вогнутой) на некотором интервале, если ее график лежит ниже (выше) касательной, проведенной в любой точке этого интервала.

Сформулируем достаточные условия. Если вторая производ­ная функции отрицательна (положительна) на интервале, то данная функция является выпуклой (вогнутой) на этом интервале.

Точкой перегиба называется такая точка графика, в которой существует касательная, и в окрестности которой график функции лежит по разные стороны касательной. Точка перегиба отделяет выпуклую часть графика от вогнутой.

Достаточные условия точки перегиба формулируются следующим образом. Если в некоторой точке определена первая производная и при переходе через эту точку вторая производная меняет свой знак, то такая точка является абсциссой точки перегиба.

Находим вторую производную.

= = .

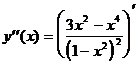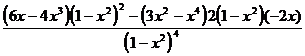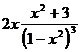Находим нули и точки разрыва второй производной, интервалы знакопостоянства второй производной. Определяем интервалы выпуклости и вогнутости функции.

Вторая производная равна нулю только в одной точке: х=0.

Вторая производная имеет точку разрыва в точках: х=-1, х=1.

Как и в предыдущем случае определяем интервалы знакопостоянства, и по знаку второй производной делаем вывод о выпуклости или вогнутости функции. Результаты удобно свести в таблицу. В таблице выпуклость функции будем обозначать символическим знаком Ç , вогнутость знаком È .

х	(-¥;-1)	(-1;0)	(0;1)	(1;+ ¥)
у¢¢	+	-	+	-
у	È	Ç	È	Ç

Определим точки перегиба.

Вторая производная меняет знак в точках: х=-1; х=0; х=1.

Однако в точках х=-1 и х=1 функция не определена. Поэтому точкой перегиба является единственная точка х=0. Значение функции в этой точке у(0)=0.

С учетом исследования на выпуклость и вогнутость подправляем полученный ранее график плавной кривой. Таким образом, получаем окончательный вид графика функции.

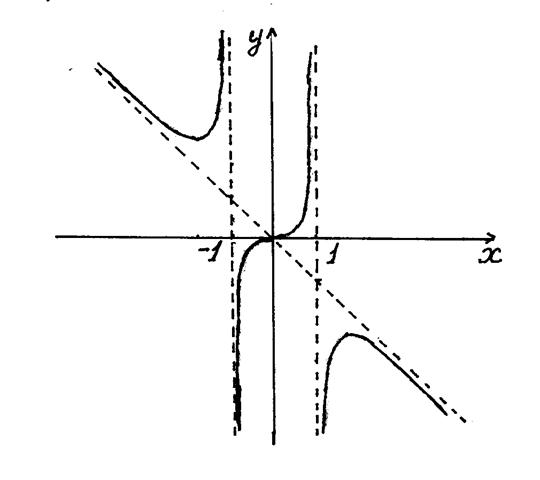
В заключение заметим, что полученный график является лишь сжатой и наглядной формой сводки результатов исследования функции. Этот график можно еще уточнять. В тоже время, найденные асимптоты позволяют судить о поведении графика за пределами области изображения на приведенном рисунке.

Задача.

Методами дифференциального исчисления провести полное исследование функции и построить ее график: .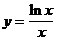

1.Область определения функции.

Функция 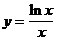определена при x>0.

2. Четность, нечетность функции.

Поскольку функция не определена при x 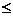0, то данная функция является функцией общего вида.

3. Нули, точки разрыва, точки пересечения графика с осями координат.

Нули функции. Решаем уравнение y(x)=0. Имеем: 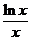=0; x=1. Следовательно, исследуемая функция обращается в ноль в единственной точке x=1.

Данная функция непрерывна на всей области допустимых значений.

Точка пересечения с осью Х, точка х=1.

Поскольку функция не определена при х=0, то ее график не пересекается с осью Y.

4. Интервалы знакопостоянства функции.

В области допустимых значений знак функции может меняться в единственной точке х=1. Точка х=1 разбивает область допустимых значений на два интервала (0;1) и (1; ¥). Определяем знак функции на каждом интервале и результаты сводим в таблицу:

x	(0;1)	(1;+¥)
y	-	+

5. Асимптоты графика функции.

А. Вертикальные асимптоты.

В своей области определения функция непрерывна. Поэтому асимптоты могут быть только на границе области определения.

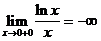. Итак, прямая х=0 – это вертикальная асимптота.

Б. Наклонные асимптоты.

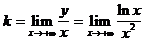. В этом пределе неопределенность вида 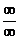. Применяем правило Лопиталя: 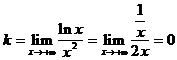. Поскольку k=0, то :

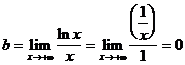. (При вычислении предела использовано правило Лопиталя.)

Таким образом уравнение асимптоты при 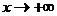имеет вид

y=0.