В следующем задании требуется провести полное исследование функции и построить ее график.

Задача.

Методами дифференциального исчисления провести полное исследование функции и построить ее график:

.

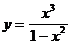Эту задачу мы рассмотрим более подробно. Непосредственно в ходе решения мы будем приводить некоторые факты теории. План исследования функции состоит из следующих шагов:

1. Область определения функции. (Для элементарной функции подразумевается естественная область определения – множество значений аргумента, в которых значение функции можно вычислить.)

Исследуемая функция 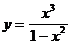определена на всей числовой оси за исключением тех точек, где знаменатель обращается в ноль.

Найдем эти точки: ; .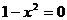

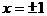Следовательно, областью определения данной функции является вся числовая ось за исключением точек .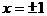

2. Четность, нечетность функции.

Напомним, что: функция называется четной, если y(-x)=y(x); функция называется нечетной, если y(-x)=-y(x). Напомним, что график четной функции симметричен относительно оси Y, график нечетной функции симметричен относительно начала координат. Если функция не является ни четной, ни нечетной, то говорят, что данная функция является функцией общего вида.

Для исследуемой функции имеем: ;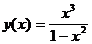

.

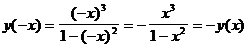Следовательно, исследуемая функция является нечетной.

3. Нули функции, точки разрыва функции, точки пересечения графика функции с осями коор­динат.

Для определения нулей функции решаем уравнение y(x)=0.

Имеем: 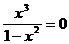; x=0. Следовательно, исследуемая функция обращается в ноль в единственной точке x=0.

Элементарная функция имеет точки разрыва только в тех точках, где она не определена. Следовательно, исследуемая функция имеет две точки разрыва , .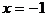

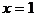График функции пересекается с осью Х в тех точках, где она равна нулю. Эти точки уже найдены.

Определим точку пересечения с осью Y. Имеем y(0)=0.

Отметим, что в данной задаче точка пересечения с осью Х и точка пересечения с осью Y совпали, то есть график функции проходит через начало координат.

4. Интервалы знакопостоянства функции.

Сначала напомним следующий факт.

Функция может изменить свой знак лишь при переходе через такие точки, в которых она равна нулю или имеет точку разрыва.

Исследуемая функция равна нулю при х=0. Имеет точки разрыва при х=-1 и х=1. Эти точки разбивают числовую ось на интервалы: (-¥;-1); (-1;0); (0;1); (1; ¥). На каждом из интервалов функция сохраняет постоянный знак. Чтобы определить знак функции на любом интервале, достаточно вычислить ее значение в любой точке интервала. Например, определим знак на интервале (0;1). Возьмем точку 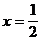, лежащую на этом интервале. Вычислим 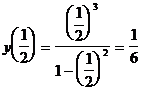>0. Следовательно, исследуемая функция положительна на интервале (0;1). Аналогично исследуются знаки функции на остальных интервалах. Результаты удобно свести в таблицу.

x (интервал изменения)	(-¥;-1)	(-1;0)	(0;1)	(1; ¥)
у (знак функции)	+	-	+	-

5. Асимптоты графика функции.

А. Вертикальные асимптоты.

Напомним, что прямая х=а является вертикальной асимптотой графика функции у=у(х), если хотя бы один из пределов 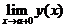или 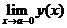равен бесконечности. Прямая х=а может быть (а может и не быть) вертикальной асимптотой только, если а - точка разрыва функции.

В исследуемой функции имеются две точки разрыва. При стремлении к этим точкам знаменатель дроби стремится к нулю, а числитель к ненулевой конечной величине. Следовательно, выражение будет стремиться к бесконечности. Знак бесконечности можно определить из таблицы интервалов знакопостоянства функции. Например, в окрестности точки х=-1 (x<-1) функция положительна. Следовательно

= .

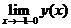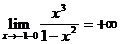Аналогично:

= ;

= ;

= .
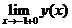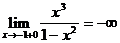
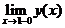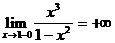
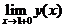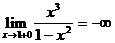