Алгоритм экспертных операций оценки качествапродукции

В литературе предложено несколько описаний алгоритма получения коллективной экспертной оценки. Эти алгоритмы в деталях несколько отличаются друг от друга. Сопоставительный анализ, проведенный Азгальдовым Г. Г. и Райхманом Э. П., показал, что для целей оценки качества товаров может быть предложен нижеследующий наиболее общий алгоритм экспертных операций оценки качества продукции:

1 Этапподготовительный

1.1 Формирование рабочейгруппы.

1.2 Формирование экспертнойгруппы.

1.3 Классификация продукции ипотребителей.

1.4 Построение структурной схемы показателейкачества.

2 Этап получения индивидуальных экспертныхоценок.

2.1 Выбор процедуры назначения оценокэкспертами.

2.2 Выбор метода получения информации от эксперта и подготовка необходимых для опроса документов (анкет, пояснительныхзаписок).

2.3 Опросэкспертов.

3 Этап получения коллективных экспертныхоценок.

3.1 Обобщение индивидуальных экспертныхоценок.

3.2 Определение согласованности индивидуальных экспертныхоценок.

3.3 Определение объективности коллективных экспертныхоценок.

С помощью этого алгоритма исключаются ошибки при опросе экспертов, и повышается достоверность результатов экспертизы.

Математико-статистические методыобработки экспертныхоценок

Математико-статистические методы обработки экспертных оценок предназначены для повышения достоверности результатов оценки качества товаров экспертами.

Подразделяются на четыре подгруппы методов: ранжирования, непосредственной оценки, последовательных предпочтений и парных сравнений.

Методранжирования

Предназначен для решения многих практических задач, когда объекты не поддаются непосредственному измерению. Кроме того, отдельные объекты, характеризующиеся различной природой, оказываются несоизмеримыми, так как у них нет общей меры сравнения.

Процедура ранжирования состоит в расположении объектов экспертом в наиболее рациональном порядке и присвоении им определенного ранга в виде числа натурального ряда. При этом ранг 1 получает наиболее предпочтительный объект, а ранг nнаименее предпочтительный. В результате получается шкала порядка, в которой число рангов равно числуобъектов.

При наибольшем числе параметров (n< 10) процедура ранжирования не представляет какие-либо трудности. В случаях же, когда n> 10, применяются различные приемы облегчения этой процедуры. Чаще всего при экспертизе качества используется следующий прием.

Из перечня параметров, содержащихся в предложенной эксперту анкете, он выбирает один, который считает самым важным и присваивает ему ранг 1. Этот параметр затем вычеркивается из перечня. Аналогичным образом из оставшегося перечня эксперт опять выбирает параметр, который он считает самым важным, и присваивает ему ранг 2 и т.д.

После первоначального ранжирования производится операция преобразования рангов. Заключается она в том, что для всего упорядоченного ряда параметров числовая последовательность рангов заменяется обратной, т.е. минимальный ранг 1 получает наименее важный, находящийся в конце ряда параметр, следующий от конца ранг 2 и т.д., а наиболее важный параметр – самый высокий ранг n. Необходимость в первоначальной ранжировке и последующем ее преобразовании объясняется тем обстоятельством, что эксперту психологически удобнее выбирать из перечня параметры, начиная именно с наиболее, а не с наименееважного.

Если два объекта имеют одинаковые ранги, то им приписывают так называемые стандартизированные ранги, которые рассчитываются как средние суммы мест объектов с одинаковыми рангами.

Например, шести объектам присвоены следующие ранги

объекты1 2 3 4 5 6

ранги 1 2 4 5 3 6.

Объекты 2 и 5 поделили 2 и 3 места. Их стандартизированный ранг будет равен (2 + 3) / 2 = 2,5.

Объекты 3; 4 и 6 поделили 4; 5 и 6 места, а их стандартизированный ранг равен 5

(4 + 5 + 6) / 3 = 5

В результате получается следующая ранжировка

1 2 3 4 5 6

1 2.5 5 5 2.5 5.

Таким образом, сумма рангов Sn, полученная в результате ранжирования nобъектов, будет равна сумме чисел натурального ряда

где xi– ранг iобъекта.

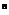
Sn= åxi

I=1

= n(n+ 1) /2 , (5)