Механический смысл производной
Положим, что материальная точка движется прямолинейно по закону 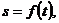 тогда ее средняя скорость за промежуток времени
тогда ее средняя скорость за промежуток времени 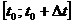 вычисляется по формуле:
вычисляется по формуле:
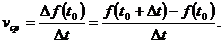
Как известно, мгновенной скоростью в момент времени t0 называется предел (если он существует), которому стремится средняя скорость за промежуток времени 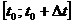 при
при 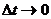 , т.е.
, т.е.
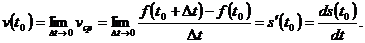
Таким образом, мгновенная скорость движения материальной точки в любой момент времени t есть производная от пути s по времени t.
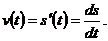
В этом состоит физический смысл производной.
Пример. Найдем скорость движения материальной точки в момент времени t = 4, если закон движения задан формулой:
| |
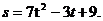
Решение. Найдем по определению: 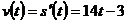 , тогда
, тогда 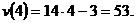
Правила дифференцирования
Если функции u(x) и v(x) имеют производные во всех точках интервала
(a; b) , то для любого х Î (a; b) выполняются следующие равенства:
1. 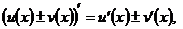
2. 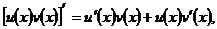
3. 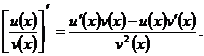
Следствие. Постоянный множитель можно выносить за знак производной:
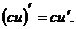
Формулы дифференцирования
| № п/п | ||||||||||
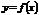 | C | х | хп | 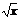 | 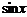 | 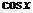 | 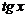 | 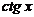 | ex | ax |
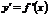 | nxn-1 | 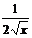 | cosx | -sin x | 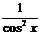 | 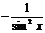 | ex | ax 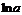 |
| № п/п | ||||||
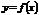 | 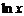 | 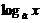 | arcsinx | arccosx | arctgx | arcctgx |
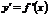 |  | 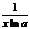 | 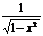 | 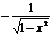 | 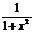 | 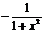 |
Пример. Вычислим производные следующих функций, используя правила и формулы дифференцирования:
1. 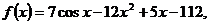
2. 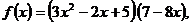
3. 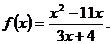
Решение.
Для решения первого примера используем правило вычисления производной алгебраической суммы функций и следствие:
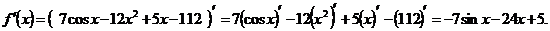
Для решения второго и третьего примеров используем правила вычисления производных произведения и отношения функций и следствие:
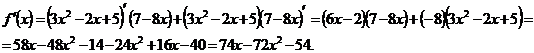
| |
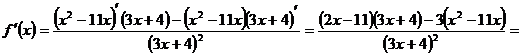
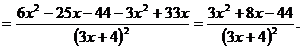
Задания.Вычислите производную функции:
1) 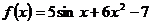
Решение. _________________________________________________
Ответ: 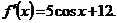
2) 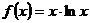
Решение. _________________________________________________
Ответ: 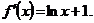
3) 
Решение. _________________________________________________
Ответ: 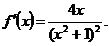
Производная сложной функции
С понятием сложной функции Вы уже неоднократно сталкивались в школьном курсе математики. Пусть даны две функции 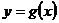 и
и 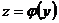 , причем область определения функции
, причем область определения функции 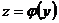 содержит область значений функции
содержит область значений функции 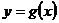 .
.
Функция, заданная формулой 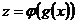 , называется сложной функцией, составленной из функций g и j или суперпозицией функций g и j.
, называется сложной функцией, составленной из функций g и j или суперпозицией функций g и j.
Пример. Для функций 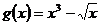 и
и 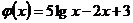 составим
составим 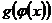 и
и 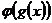 .
.
Решение.
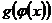
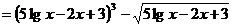 ;
;
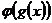
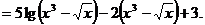
Вышеуказанный пример наглядно демонстрирует тот факт, что результат суперпозиции двух различных функций зависит от порядка, в котором эти функции следуют. Рассмотрим теорему о производной сложной функции:
Теорема. Пусть функция 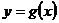 , хÎ (a; b), имеет производную в точке х0 Î (a; b), а функция
, хÎ (a; b), имеет производную в точке х0 Î (a; b), а функция 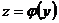 определена на интервале, содержащем множество значений функции g, и имеет производную в точке
определена на интервале, содержащем множество значений функции g, и имеет производную в точке 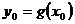 . Тогда сложная функция
. Тогда сложная функция 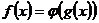 имеет производную в точке х0,, которая вычисляется по формуле:
имеет производную в точке х0,, которая вычисляется по формуле:
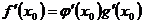
Пример. Найдем производные следующих функций:
1) 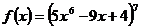 ;
;
2) 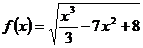 ;
;
3) 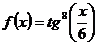 .
.
Решение.
1) Полагаем, что 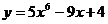 , тогда
, тогда 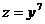 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
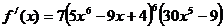 .
.
2) Полагаем, что 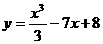 , тогда
, тогда 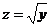 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
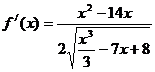 .
.
3) Имеем, что
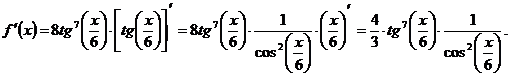
Задание.Найдите производные следующих функций:
1) 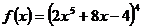
Решение.____________________________________________________________________________________________________________________________________
Ответ: 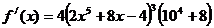
2) 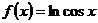
Решение.____________________________________________________________________________________________________________________________________
Ответ: 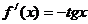
Дифференциал
Дифференциал 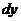 функции
функции 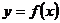 – это главная часть приращения функции
– это главная часть приращения функции 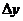 в точке х, так что
в точке х, так что 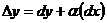 , где
, где 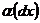 – бесконечно малая величина.
– бесконечно малая величина.
Дифференциал функции 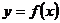 вычисляется по формуле:
вычисляется по формуле:
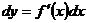 ,
,
где 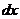 – дифференциал аргумента, равный приращению аргумента в данной точке.
– дифференциал аргумента, равный приращению аргумента в данной точке.
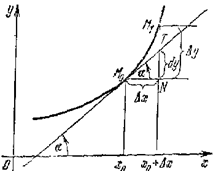 Рис. 8 Рис. 8 | Геометрический смысл дифференциала: дифференциал функции равен приращению ординаты касательной к графику функции в соответствующей точке, когда аргумент получает приращение 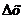 (см. рис. 8). Приближенное равенство (см. рис. 8). Приближенное равенство 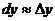 используется в приближенных вычислениях. В таких случаях значение выражения используется в приближенных вычислениях. В таких случаях значение выражения 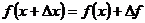 заменяют приближением: заменяют приближением: 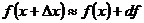 |
