Современный этап развития средств автоматизации связан с успехами микроэлектроники, созданием больших интегральных схем, микро ЭВМ, однокристальных ЭВМ, микропроцессоров.
Введение
Вряд ли сейчас можно найти сферу нашей жизни, в которую не проникли бы в том или ином виде современные устройства цифровой электроники. Их можно встретить буквально на каждом шагу. Утром нас с постели поднимает электронный будильник, а наручные электронные часы сообщают нам о начавшемся новом дне недели и даже способны сыграть несколько бодрящих мелодий. Направляясь на работу, мы выходим на улицу, и дверь подъезда обычно накрепко запирает за нами электронный замок. При входе в метро разменный автомат любезно выдает нам нужное число жетонов взамен опущенной монеты, а зоркий турникет следит за правильной оплатой проезда. В учреждении где вы работаете или учитесь, наверняка несет трудную службу ЭВМ, никогда не устающая, ничего не забывающая, хранящая в своей памяти огромный объем информации и способная быстро выдавать нужные сведения пользователю по первому требованию.
Цифровые индикаторы кассовых аппаратов и присутствующие в них оптические устройства для автоматического считывания информации, содержащейся в универсальном коде товаров; работа промышленного оборудования контролируется цифровыми электронными схемами; применение техническими специалистами в своей работе цифровых вольтметров и частотометров; обогревом вашего жилища может управлять автоматически включаемый и выключаемый термообогреватель; широко используется цифровая электроника в электронных играх и видео играх; такие бытовые приборы, как СВЧ-печи, стиральные машины и сушилки могут иметь в своем составе сложные цифровые схемы, контролируемые микропроцессорами. Вот далеко не полный перечень применения цифровых электронных устройств в нашей жизни.
В настоящее время невозможно найти какую-либо отрасль промышленности, в которой не использовались бы электронные приборы или электронные устройства измерительной техники, автоматики и вычислительной техники. Причем тенденция развития такова, что доля электронных устройств и устройств автоматики непрерывно увеличивается. Это является результатом развития интегральной технологии, внедрение которой позволило наладить массовый выпуск дешевых, высококачественных, не требующих специальной настройки и наладки микроэлектронных функциональных узлов различного назначения. Они представляют собой полупроводниковые пластины малой толщины на который в площадях в несколько квадратных миллиметров выполнены десятки тысяч электрически соединенных между собой элементов электроники (транзисторов, конденсаторов и т.д.). Причем эти элементы, как правило, получают одновременно (по групповой технологии) в едином технологическом цикле, который почти полностью автоматизирован. Поэтому стоимость интегральных схем при массовом производстве мало зависит от количества в них элементов и разброс параметров от образца к образцу сравнительно невелик.
Промышленность выпускает почти все электронные функциональные узлы необходимые для создания устройств измерительной и вычислительной техники, а также систем автоматики: интегральные электронные усилители электрических сигналов; коммутаторы; логические элементы; перемножители электрических напряжений; триггеры и т.д. на основе больших (БИС) и сверхбольших (СБИС) интегральных схем созданы и выпускают микропроцессоры и микропроцессорные комплекты, представляющие собой вычислительную машину или ее основные узлы, изготовленные в одном корпусе или в нескольких малогабаритных корпусах.
Автоматизация процессов управления, на основе дискретных управляющих устройств есть необходимый элемент современного производства. Ее широкое внедрение обеспечивает повышение производительности труда и улучшения качества продукции. Развитие целых отраслей современной науки и техники принципиально невозможно без использования средств автоматики, которая включает в себя дискретные управляющие устройства.
На качественно новую ступень развития автоматизация поднимается с появлением электронно-вычислительных машин, когда процессы управления получают программную реализацию и возникает возможность широкой автоматизации не только физической, но и умственной деятельности человека.
На железнодорожном транспорте, как и во всех отраслях народного хозяйства, широко применяется автоматизация, компьютеризация, телемеханизация производственных процессов, и прежде всего процессов управления движением поездов.
Независимо от степени сложности микросхемы и широты выполняемых ими функций, основу их структуры составляю элементарные схемы, физические принципы и особенности работы которых наиболее просто и эффективно проявляются при модернизации микросхем с помощью отдельных дискретных электронных элементов. Это способствует более глубокому пониманию принципов построения электронных устройств любой сложности, позволяет более эффективно и полно использовать их качества, упрощает процесс настройки и поиск неисправностей.
A V
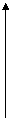







 5
5









 + 4
+ 4



 V 3 Движок Движок
V 3 Движок Движок





 5B - 2 перемещ перемещ
5B - 2 перемещ перемещ



 1 вверх вниз
1 вверх вниз
 B 0 t
B 0 t
a) б)
Рис1. а) аналоговый сигнал с выхода потенциометра
б) форма аналогового сигнала.
Электрическая цепь, показанная на рис.1.а, вырабатывает на выходе аналоговый сигнал напряжения. Если движок потенциометра перемещать вверх, напряжение между точками А и В будет плавно увеличиваться. Когда движок потенциометра перемещается вниз, напряжение плавно уменьшается от 5В до 0В. График изменения напряжения, показанный на Рис.1.б, характеризует аналоговый выходной сигнал. В левой части графика напряжение между точками А и В постепенно возрастает до 5В, в правой части напряжение постепенно снижается до 0В. Останавливая движок где-нибудь в средней части потенциометра, мы можем получит на выходе любые напряжения между 0 и 5В. Таким образом, аналоговое устройство - это такое устройство в котором сигнал на выходе меняется непрерывно при постепенном изменении сигнала на входе.
Цифровые устройства оперируют с цифровыми сигналами. На Рис.2.а изображен генератор прямоугольных импульсов.
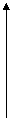

 V
V
 Генератор
Генератор






 прямоугольн Высокий уровень
прямоугольн Высокий уровень



 импульсов +5 В
импульсов +5 В









Осциллограф


 0 А
0 А
а) б) Низкий уровень
Рис2. а)—цифровой сигнал, наблюдаемый на экране осциллографа.
б)—форма цифрового сигнала.
Генератор непрерывно выдаёт сигналы прямоугольной формы, которые можно наблюдать на экране осциллографа. Как показано на Ри.2.б в цифровом сигнале имеются только два уровня напряжения: +5 и 0В. В точке А напряжение возрастает от 0 до 5В. Далее оно в течении какого-то времени остается равным +5В. В точке В напряжение быстро падает от+5В до 0В, а затем некоторое время сохраняет величину 0В. Для цифровых электронных схем, таким образом существенны только два значения напряжения. На Рис 2.б показана форма цифрового сигнала, а эти значения напряжения названы высоким и низким уровнями. Первому соответствует напряжение +5В, второму 0В. Схемы, в которых применяются сигналы только двух типов – с высокими и низкими уровнями напряжения — называются цифровыми схемами, сигналы в них изменяются скачкообразно, т.е. дискретным образом. Следовательно, цифровая система может быть описана как двоичная, и двум используемым уровням напряжения можно поставить в соответствии двоичные значения 0 и 1. Два состояния, определённые таким образом, можно интерпретировать логически как наличие или отсутствие определённого условия.
 |  |  |
В прошлом столетии (ХIХ вв.) английский математик Джордж Буль (1815—1864) разработал специальную алгебру, которая оказалась очень удобной для представления ситуации, описанной выше. Вследствие эта ветвь математики получила название булевой алгебры, которая оперирует с переменными, принимающими только два значения: 0 и 1.В ней существует множество правил и ряд теорем, которые дают возможность оперировать булевыми выражениями. Знания булевой алгебры необходимо для выполнения любой работы, связанной с проектированием цифровых систем.
Алгебра Буля была не востребована по следующие 100 лет лишь в 1938 —1940гг советский физик В.И. Шестаков, американский математик Клод Шеннон, японский ученый А. Накашима доказали возможность использования булевой алгебры при анализе и синтезе контактных схем (независимо друг от друга). Применение аппарата математической логики для решения задач дискретной техники получило существенное развитие в трудах М.А. Гаврилова, Д.А. Поспелова, В.Г. Лазарева, В.Н. Рогинского, А.Д. Закревского и др. ученых.
Большое влияние на развитие теории дискретных устройств оказало создание электронных вычислительных машин. Крупный вклад в указанную теорию и практику дискретной техники, особенно в применении к ЭВМ, внес академик В.М. Глушков, который в 1966 году возглавил 1-й в мире институт кибернетики.
Устройство ж.д. автоматики, телемеханики и связи в основном относятся к классу дискретных устройств. Первые релейные системы автоматики на транспорте появились в 30-х годах нашего столетия. На ж.д. эксплуатируется большое число разнообразных систем электрической централизации, автоматической блокировки, диспетчерской централизации систем горочной автоматики, устройств связи и др. Большинство систем имеют длительный срок службы, непрерывный характер работы и выполняют ответственные функции по обеспечению безопасности движения. Вследствие этого к ж.д. системам автоматики, телемеханики и связи предъявляют повышенные требования с точки зрения надежности, безопасности и устойчивости работы.
Некоторые определения:
1. Информация – совокупность сведений о событиях, объектах или явлениях.
2. Сообщения – совокупность знаков, содержащих ту или иную информацию.
3. Сигнал – средство перенесения информации в пространстве и времени.
4. Кодирование – построение сигнала по определенным правилам.
5. Дискретный сигнал – сигнал, представляющий собой функцию времени, принимающую только определенные дискретные значения (напр. 0 или 1).
6. Дискретное сообщение – сообщение, принимающее только некоторые определенные значения.
7. Аналоговый (непрерывный) сигнал (или сообщение) – может принимать любые значения в некотором интервале времени.
8. Алгоритм – конечный набор правил для элементарных действий в определенной последовательности над исходными данными в любой задаче при ее решении.
9. Дискретный элемент – некоторая минимальная совокупность деталей, объединенных в общую схему для выполнения какой-либо функции и имеющую релейную характеристику. У элемента с такой характеристикой и изменение входной величины х вызывает скачкообразное изменение выходной величины z, принимающей лишь два дискретных значения: 0 и 1.
Таблица Таблица Таблица Таблица
Таблица 2.
| № набора | х1 | х2 | х3 | f |
Каждому набору переменных соответствует определенное значение функции.При трех переменных можно образовать восемь наборов. Следовательно, приведенная в табл.2 функция определена на 8 наборах. Каждый набор представляет собой трехразрядное двоичное число. Если ФАЛ содержит п переменных, двоичные числа будут п-разрядные, и→, общее число наборов будет N = 2п.
Таблицу, в которой для всех наборов переменных приводятся значения ФАЛ, наз. таблицей истинности. При п переменных таблица содержит 2п строк (по числу наборов), п столбцов (по числу переменных) и один столбец значений функции. Крайний левый столбец (номер набора) является десятичным эквивалентом двоичного набора переменных.
3. При графическом способе наборами значений переменных ФАЛ сопоставляются точки п-мерного пространства. Множество 2п наборов определяет множество вершин п-мерного единичного куба. Вершинам куба соответствуют наборы значений переменных и приписаны значения функции на этих наборах, т.е. областью определения ФАЛ, зависящей от п-переменных, является множество вершин единичного п-мерного куба.
 х2 Функция f (x1,x2,x3) ,заданная
х2 Функция f (x1,x2,x3) ,заданная

 таблицей истинности (табл. 2)
таблицей истинности (табл. 2)

 010 0 0 может быть задана графически.
010 0 0 может быть задана графически.
 | |||||
 |  | ||||


 110 0 111 1
110 0 111 1
 |  |

 001
001

 000 0 1 х3
000 0 1 х3
 | |||
 | |||


 100 0 0 101
100 0 0 101
 |
х1
Рис. 4 Графический способ задания ФАЛ.
4. При координатном способе функцию задают в виде координатной карты состояния, которую называют Карта Карно. Карты представляют собой прямоугольные таблицы, разделенные горизонтальными и вертикальными линиями на клетки. Общее число клеток соответствует числу наборов функции. Все переменные функции разбивают на 2 группы. Одна группа переменных определяет выбор строки, другая – столбца. На пересечении строки и столбца находится клетка, в которую записывают значение функции при соответствующем наборе переменных. Разделение переменных на группы осуществляется так, чтобы в соседних клетках наборы различались только значением одной переменной.
 x2x3
x2x3



 x1 00 01 11 10
x1 00 01 11 10
 0 1 1
0 1 1
1 1
Рис.5 Функция f(x1,x2x3) заданная табл. истинности (табл. 2) ,представлена картой Карно.
5.При числовым способе каждому набору переменных ставят в соответствие определенное число в двоичной системе и присваивают десятичный номер, равный эквиваленту двоичного числа. Функцию задают в виде десятичных номеров тех наборов переменных, на которых она принимает значение 1.
Функция f (х1, х2, х3), приведенная в табл.2, может быть задана числовым способом так: f = {1, 3, 7} х1 х2 х3. Обратить особое внимание на порядок следования переменных.
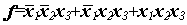 |
6.При аналитическом (алгебраическом) способе функцию задают в виде алгебраического выражения, показывающего, какие и в какой последовательности должны выполнятся логические операции над аргументами. Алгебраические выражения может быть составлено из наборов аргументов, на которых функция принимает значение 1, или из наборов аргументов, на которых она принимает значение 0. Аналитическое выражение для функции f (х1, х2, х3), заданной табл.2, имеет вид:
Операции алгебры логики
Техническая интерпретация логических выражений может быть насмотрена как аналогия между высказываниями и электрическими переключателями, поскольку и те и другие имеют двоичную природу.
Любое истинное высказывание изображается в виде замкнутого, а любое ложное высказывание- в виде разомкнутого контакта. На основе принятой аналогии любую логическую функцию можно изобразить в виде некоторой переключательной схемы (вот почему логические функции часто называют переключательными). Рассмотрим переключатель, показанный на рис.6
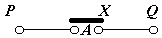 x x | f |
Рис.6. а) – простейшая переключательная контактная схема
б) – таблица истинности f = х
Этот переключатель связывает между собой две точки: Р и Q. Состояние переключателя может быть выражено с помощью булевой переменной Х, которая может принимать два значения 0 и 1. Если переключатель разомкнут, то Х = 0, а если замкнут то Х = 1. Состояние соединения РQ может быть выражено с помощью булевой функции f, которая принимает одно из двух значений: 0 или 1. Если связи между точками Р и Q нет, то f = 0, если есть - f = 1. Эти результаты сведены в таблицу истинности (Рис. 6б), из которой ясно, что f = х.
2. Операция И (логическое умножение, конъюнкция)
Два переключателя А и В соединены последовательно и связывают точки Р и Q (Рис.7). Пусть состояния переключателей выражаются с помощью двух булевых переменных х1 и х2. Если переключатель А разомкнут, то х1 = 0, если разомкнут, то х1 = 1. Аналогично, х2 = 0 или х2 = 1, в зависимости от того, разомкнут или замкнут переключатель В. Состояние соединения РQ выражается с помощью булевой функции f, значение которой зависит от наличия связи между точками Р и Q (рис 7.а)
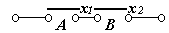 P Q
P Q
№ | x1 | x2 | f | |||


 б)
б)

 x1 & f
x1 & f
 x2
x2
 |
в)
Рис . 7. а)- переключательная контактная схема, реализующая операцию И;
б)- таблица истинности функции И.
в)- условное обозначение элемента И.
Существует четыре возможные комбинации значений переменных х1 и х2. .
Они сведены в таблицу истинности (рис 7б). Функцию И называют функцией булевого (логического) умножения, конъюнкцией и записывают в виде: f = х1 * х2 или f = х1 ^ х2. В цифровых системах функция “И” реализуется с помощью электронной схемы, называемой элементом И. Условное обозначение элемента И на функциональных схемах изображено на Рис.7в. Функция И истинна, если истинны все ее аргументы. Исходя из этого определения, можно вывести такие свойства функции И:
1) результат многократного логического умножения аргумента самого на себя равен исходному аргументу: х * х * х….х = х;
2) логическое произведение двух аргументов из которых первый заведомо является истинным, равно второму аргументу: 1 * х = х
3) логическое произведение двух аргументов, из которых один заведомо является ложным, равно нулю: 0 * х = 0;
4)
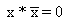 |
логическое произведение некоторого аргумента х и его отрицания х равно нулю:
3.Операция НЕ (логическое отрицание, инверсия)
Рассмотрим переключательную схему на Рис.8а. Она состоит из двух связанных переключателей: если один из них замкнут, то другой обязательно разомкнут. На Рис.8а разомкнутый переключатель представляется булевой переменной Х, замкнутый – булевой переменной Х. Для верхнего переключателя Х = 0, когда этот переключатель разомкнут, а для нижнего переключателя, который замкнут, когда верхний разомкнут, Х = 1. Говорят, что Х есть инверсия Х или НЕ Х. Следовательно, черта над булевой переменной Х означает инверсию (или отрицание) переменной.
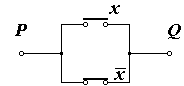
 х х | x | f |
а) б)
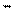
Рис.8 а) – переключательная схема функции f = х + х
 б) - таблица истинности f = х + х
б) - таблица истинности f = х + х
Связь между точками Р и Q существует всегда т.к. f = 1 в любом случае, независимо, верхний или нижний переключатель замкнут: т.е. х + х = 1. Уравнение двойственное по отношению к любому булевому уравнению, получается заменой нужного знака “ + “ не “ * “ и заменой всех 1 на 0 и наоборот. По отношению к вышеприведенному уравнению эта процедура приводит к х * х = 0


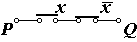 x x | x | f |
а) б)
 Рис.9 а) – переключательная схема функции f = х * х
Рис.9 а) – переключательная схема функции f = х * х
 б) – таблица истинности f = х * х
б) – таблица истинности f = х * х
Инвертор может быть реализован с помощью электронной схемы, условное обозначение которой приведена на рис.9.
 х х | f=x |


 1
1



 |
Условное обозначение инвертора и его табл. истинности.
Функция НЕ истинна, если ложен её аргумент, и наоборот.
Эта функция обладает следующими свойствами:
1)двойное отрицание (а также любое четное количество отрицаний) некоторого аргумента х равно самому аргументу: х=х;
2)тройное отрицание (а также любое нечетное количество отрицаний) некоторого аргумента х равно отрицанию этого аргумента х=х;
3)если имеется некоторое логическое равенство, то отрицание обеих его частей не нарушает этого равенства, т.е. если f1 = f2, то и f1 = f2.
1.Операция ИЛИ (логическое сложение, дизъюнкция.)
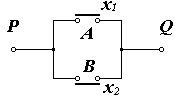 На рис. 10 два переключателя А и В соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения Р Q выпрямляются с помощью булевых переменных х1, х2 и f соответственно. Если оба переключателя А и В разомкнуты, то х1=0, х2=0 и ясно, что связи между точками Р Q нет;→ f=0. С другой стороны, если переключатель А замкнут, а В разомкнут, то х1=1, х2=0 и связь между точками Р иQ осуществляется с помощью переключателя А,→f=1.
На рис. 10 два переключателя А и В соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения Р Q выпрямляются с помощью булевых переменных х1, х2 и f соответственно. Если оба переключателя А и В разомкнуты, то х1=0, х2=0 и ясно, что связи между точками Р Q нет;→ f=0. С другой стороны, если переключатель А замкнут, а В разомкнут, то х1=1, х2=0 и связь между точками Р иQ осуществляется с помощью переключателя А,→f=1.
а)
  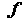   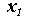 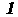 № № | х1 | х2 | f |
  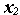  0 0 | |||
 1 1 | |||
б) г)
Булево Двоичное
сложение сложение
0+0=0 0+0=0
0+1=1 0+1=1
1+0=1 1+0=1
1+1=1 1+1=0 (перенос 1)
в)
Рис.10 а)-переключательная контактная схема функции ИЛИ
б)-таблица истинности функции ИЛИ
в)-правила двоичного и булевого сложения
г)-условное обозначение элемента ИЛИ
Функцию ИЛИ называют функцией логического сложения, дизъюнкцией
и записывают в виде; f=х1+х2 или f=х1 v х2. В цифровых системах функция ,,ИЛИ'' реализуется с помощью электронной схемы, называемой элементом ИЛИ (условное обозначение которого приведено на рис.10 г).
Функция ИЛИ истинная, если истинен хотя бы один из её аргументов.
Исходя из этого определения дизъюнкции, можно указать её основные свойства:
1)результат многократного логического сложения некоторого аргумента с самим собой равен исходному аргументу: х+х+…+х=х;
2)логическая схема двух аргументов, из которых первой заведомо является ложным, равно второму аргументу: 0+х=х;
3)логическая схема двух аргументов, из которых один заведомо является истинным равно единице: 1+х=1;
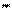 4)логическая сумма некоторого аргумента и его отрицания равна единице: х+х=1
4)логическая сумма некоторого аргумента и его отрицания равна единице: х+х=1
Основные законы булевой алгебры.
В булевой алгебре имеются четыре основных закона, регламентирующих порядок выполнения операций И, ИЛИ, НЕ в любом логическом выражении и обеспечивающих адекватное преобразование логических функций из одной формы в другую.
1. Переместительный закон справедлив как для дизъюнкции, так и для конъюнкции: от перемены мест слагаемых (сомножителей) их логическая сумма (произведение) не изменится. Так, для двух входных переменных можно записать: х1 + х2 = х2 + х1; х1 * х2 = х2 * х1 .
Переместительный закон будет справедлив при любом значении входных переменных.
2. Сочетательный закон также как и переместительный является симметричным:
а) при логическом сложении нескольких аргументов группу слагаемых можно заменить их логической суммой:
x1+x2+x3=x1+(x2+x3)=x2+(x1+x3)=x3+(x1+x2);
б) при логическом умножении нескольких аргументов группу сомножителей можно заменить их логическим произведением:
x1*x2*x3=x1*(x2*x3)=x2*(x1*x3)=x3*(x1*x2)
3. Распределительный закон.
а) распределительный закон 1-го рода: произведение суммы нескольких аргументов на какую-либо (логическую) переменную равно сумме произведений каждого слагаемого на эту переменную:
(x2+x3)*x1=x1*x2+x1*x3
б) распределительный закон П-го рода: сумма некоторой логической переменной и произведение нескольких аргументов равна произведению сумм каждого сомножителя этой переменной:
x1+x2x3=(x1+x2)*(x1+x3)
Док-во:
 (х1+х2)*(х1+х3)=х1*х1+х1*х3+х1*х2+х2*х3=х1+х1*х3+х1*х2+х2*х3=х1(1+х3+х2)+х2*х3=х1+х2*х3 —что и требовалось доказать 1
(х1+х2)*(х1+х3)=х1*х1+х1*х3+х1*х2+х2*х3=х1+х1*х3+х1*х2+х2*х3=х1(1+х3+х2)+х2*х3=х1+х2*х3 —что и требовалось доказать 1
4. Закон инверсии (правило Де Моргана), симметричен относительно дизъюнкции и конъюнкции:
а) отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов:



 х1+х2+…+хn=х1*х2*…*хn
х1+х2+…+хn=х1*х2*…*хn
Доказательство закона не представляет трудностей, т.к. условия обращения в нуль как левой, так и правой частей закона состоит в том, чтобы был истинным хотя бы один аргумент.



 б) отрицание логического произведения нескольких аргументов равно логической сумме отрицания этих же аргументов:
б) отрицание логического произведения нескольких аргументов равно логической сумме отрицания этих же аргументов:
x1*x2*…xn=x1+x2+…+xn
Справедливость этого закона следует из того, что условие обращения в единицу обеих частей заключается в том, чтобы был ложным хотя бы один аргумент из любого конечного их множества.
Следствие из законов булевой алгебры
Из рассмотренных выше законов выведем ряд следствий, которые сформулируем в виде правил.
1. Правило старшинства логических операций. По аналогии с арифметическими действиями будем считать отрицание – логическим действием первой ступени (старшей логической операцией), конъюнкцию – действием второй ступени, а дизъюнкцию – действием третьей ступени (младшей логической операцией).
2. 

 Правило склеивания обеспечивает упрощение логических выражений:
Правило склеивания обеспечивает упрощение логических выражений:
(x1+x2)*(x1+x2)=1 x1*(x1+x2)=x1


 x1*x1+x1*x2+x1*x2+0=x1*(1+x2+x2)=x1 x1(x2+x2)=x1
x1*x1+x1*x2+x1*x2+0=x1*(1+x2+x2)=x1 x1(x2+x2)=x1

 1 1
1 1
3. Правило поглощения также позволяет упростить выражения:
x1+x1*x2=x1 x1(x1+x2)=x1


 x1(1+x2)=x1 x1*x1+x1*x2=x1(1+x2)=x1
x1(1+x2)=x1 x1*x1+x1*x2=x1(1+x2)=x1
1 1 1
Канонические формы ФАЛ.
Важным этапом построения сложных дискретных устройств является определения способа соединения между собой логических элементов, обеспечивающих работу устройства в соответствии с заданным законом функционирования. Однако, любая функция алгебры логики выражается через исходные функции неоднозначно. Поэтому требуется найти такую форму её представления, которая позволяет построит наиболее простую электрическую схему. При решении этой задачи заданную функцию алгебры логики дискретного устройства вначале оказывается удобным представить в некоторой исходной канонической форме, которую называют нормальной.
Каноническими формами преставления функции алгебры логики является
СДНФ и СКНФ, ДНФ и КНФ.


 ДНФ –это дизъюнкция конечного числа элементарных конъюнкций. Конъюнкцию называют элементарной, если она представляет собой произведения переменных без скобок: например:
ДНФ –это дизъюнкция конечного числа элементарных конъюнкций. Конъюнкцию называют элементарной, если она представляет собой произведения переменных без скобок: например:
F(х1,…х4)=х1х