Взаимосвязь развития познавательных процессов и математических способностей ребенка

Для развития математических способностей важно избира­тельное восприятие специфических характеристик внешне­го мира: формы, размера, пространственного расположенияи количественных характеристик объектов. Очевидно, что из этих характеристик быстрее и легче всего воспринимаются сенсорикой форма, размер и пространственное расположение. Как уже отмечалось ранее, для адекватного выделения и вос­приятия ребенком количественных характеристик требуется специальное обучение. Для формирования и развития воспри­ятия необходимо обеспечить ребенку возможность обследова­ния воспринимаемого объекта, способы и средства создания его адекватной модели (его подобия) сначала в вещественной фор­ме во внешней деятельности, чтобы обеспечить затем его ин-териоризацию во внутреннюю форму — представление. Таким образом будет происходить накопление запаса образов вообра­жения. В продуктивном восприятии предмета наиболее важ­ным для ребенка является действие, которым он при этом поль­зуется: деятельность тактильного обследования должна пред­шествовать деятельности визуального наблюдения и анализу наблюдаемого предмета, явления и т. п.

Такую последовательность действий ребенка с изучаемым материалом легко обеспечить при преимущественной работе с геометрическим материалом, поскольку для любой геомет­рической фигуры или геометрического тела несложно сконст­руировать самые разнообразные модели из самого различного материала, причем все они будут адекватно отражать основ­ные его характеристики. Например, квадрат из бумаги, па­лочек, пластилина, конструктора, ткани, нитки, а также его рисунок на песке, глине, восковой дощечке, классной доске и т. д. будет моделью одного и того же понятия, отражающей его основные свойства: наличие четырех равных прямолиней­ных сторон и четырех прямых углов. Все перечисленные моде­ли ребенок может выполнить самостоятельно, собственными руками, а затем провести целую серию наблюдений (выражая их словесно) при обследовании любой из них — сравнить дли­ны сторон, сосчитать их, сравнить форму и равенство углов, а также установить и многие другие его свойства путем про­стых манипуляций с моделью.

Способом организации такой познавательной деятельности ребенка является соответствующим образом разработанное за­дание (упражнение), выполняя которое, ребенок осуществля­ет продуктивное восприятие объекта (обследование, модели­рование) и осмысление воспринятой сенсорной информации (сопровождает чувственное восприятие словом).

Упражнение 1

Цель. Подготовить детей к последующей моделирующей деятельно­сти посредством простых конструктивных действий, актуализировать счетные умения, организовать внимание.

Материалы. Счетные палочки двух цветов, фланелеграф с картонны­ми моделями палочек у педагога.

Задание.

— Возьмите из коробки столько палочек, сколько у меня. Положите пе­ред собой так же (II). Сколько палочек? {Две.)

— У кого палочки одного цвета? У кого разного цвета? Какого цвета у тебя палочки? (Одна — красная, одна — зеленая.)

— Один да один. Сколько вместе? (Два.)

Упражнение 2

Цель. Организовать конструктивную деятельность по образцу, упраж­нять в счете, развитие воображения, речевой деятельности. Материалы. Счетные палочки, фланелеграф. Задание.

— Возьмите еще одну палочку и положите ее сверху (II). Сколько ста­ло палочек? Сосчитаем. (Три.)

— На что похожа фигура? (На ворота, на букву П). Кто знает слова, начинающиеся на П?

Дети говорят слова.

Упражнение 3

Цель. Развивать наблюдательность, воображение и речевую деятель­ность; формировать умение оценивать количественную характеристику видоизменяющейся конструкции (без изменения количества элементов); подготовка к правильному восприятию смысла арифметических действий.

Материалы. Счетные палочки, фланелеграф.

Задание.

— Верхнюю палочку переложите так: "Н Изменилось ли количество палочек? Почему не изменилось? (Палочку переставили, но не убрали и не добавили.)

— На что теперь похожа фигура? (На букву Н.) Назовите слова, начинаю­щиеся на Н.

Упражнение 4

Цель. Формировать конструкторские умения, воображение, память и внимание.

Задание.

— Сложить из этих трех палочек разные фигурки.

Дети складывают фигурки и буквы. Называют их, придумывают слова. Кто-нибудь из детей обязательно сложит треугольник.

Упражнение 5

Цель. Формировать образ треугольника, первичное обследование мо­дели треугольника.

Материалы. Счетные палочки, фланелеграф.

Способ выполнения. Педагог предлагает всем сложить такую фигуру:А

— Сколько палочек вам понадобилось для этой фигуры? (Три.) Кто знает, что это? (Треугольник.) Кто знает, почему он так называется? (Три угла.)

Если дети не могут назвать фигуру, педагог подсказывает ее название и просит детей объяснить, как они его понимают.

Педагог просит обвести фигуру пальцем, сосчитать углы (вершины), касаясь их пальцем.

Упражнение 6

Цель. Закреплять образ треугольника на кинестезическом и визуаль­ном уровне. Распознавать треугольник среди других фигур (объем и ус­тойчивость восприятия). Обводить и штриховать треугольники (развивать мелкие мышцы руки).

Материалы. Рамка-трафарет с прорезями в форме геометрических фи­гур, бумага, карандаши.

Примечание. Задание является проблемным, поскольку на исполь­зуемой рамке есть несколько треугольников и фигур, на них похожих ост­рыми углами (ромб, трапеция).

Задание.

— Найдите на рамке треугольник. Обведите его. Заштрихуйте треуголь­ник по рамке. (Штриховка производится внутри рамки, кисть движется сво­бодно, карандаш «стучит» по рамке.)

Упражнение 7

Цель. Закреплять визуальный образ треугольника. Распознавать нуж­ные треугольники среди других треугольников (точность восприятия). Раз­вивать воображение и внимание, мелкую моторику.

Материалы. Трафарет, бумага, карандаши.

Задание.

— Посмотрите на этот рисунок: Кошка-мама, кот-папа и котенок, каких фигур они составлены? (Круги и треугольники.)

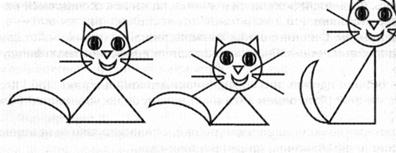
— Кто нарисовал такой треугольник, какой нужен для котенка? Для кош­ки-мамы? Для кота-папы? Дорисуйте своего кота.

Дети дорисовывают, используя тот треугольник, который у них есть, т. е. у каждого получается свой кот. Затем они дорисовывают остальных кошек, ориентируясь на образец, но самостоятельно.

Педагог обращает внимание на то, что кот-папа самый высокий.

— Правильно поставьте рамку, чтобы кот-папа получился самый вы­сокий.

Данное упражнение не только способствует накоплению у ребенка за­пасов образов геометрических фигур, но и развивает его пространст­венное мышление, поскольку фигуры на рамке расположены в различных положениях и, чтобы найти нужную, необходимо узнать ее в другой пози­ции, а затем повернуть рамку для ее рисования в такой позиции, которую требует рисунок.

Приведенные фрагменты занятий показывают способ по­строения взаимосвязанной системы заданий для формирова­ния и развития сенсорных познавательных способностей на математическом материале. Очевидно, что деятельность ре­бенка в данном фрагменте является также организующей его внимание и стимулирующей воображение.

Перейдем к другой группе познавательных способностей — к интеллектуальным способностям. Как уже было сказано, в их основе лежит развитое мышление. Процесс развитиямышления методически состоит в формировании и развитии обобщенных приемов умственных действий (сравнение, обоб­щение, анализ, синтез, сериация, классификация, абстра-гирование, аналогия и др.), что является общим условием функционирования самого мышления как процесса в любой области познания, в том числе и в математике. Безусловным является то, что сформированность умственных действий яв­ляется абсолютной необходимостью для развития матема­тического мышления, не случайно эти умственные действия именуются также приемами логических умственных дейст­вий. Их формирование стимулирует развитие математических способностей ребенка. Одним из самых значительных иссле­дований в этой области явилась работа швейцарского психо­лога Ж. Пиаже «Генезис числа у ребенка»¹, в которой автор достаточно убедительно доказывает, что формирование поня­тия числа (а также и арифметических операций) у ребенка кор­релятивно развитию самой логики: формированию логических структур, в частности формированию иерархии логических классов, т. е. классификации, и формированию асимметрич­ных отношений, т. е. качественных сериаций. Классификация и сериация являются приемами умственных действий, форми­рование которых невозможно без предварительного развития у ребенка операций сравнения, обобщения, анализа и синте­за, абстрагирования, аналогии и систематизации.

Легко показать на приведенном выше фрагменте занятия, что каждое из приведенных упражнений одновременно «работает» также на формирование всех этих мыслительных приемов. На­пример, упражнение 1 учит ребенка сравнивать; упражнение 2 — сравнивать и обобщать, а также анализировать; упражнение 3 учит анализу и сравнению; упражнение 4 — синтезу; упражне­ние 5 — анализу, синтезу и обобщению; упражнение б — фак­тическая классификация по признаку; упражнение 7 учит срав­нению, синтезу и элементарной сериаций.

Таким образом, математическое содержание оптимально для развития всех познавательных способностей (как сенсор­ных, так и интеллектуальных), приводит к активному разви­тию математических способностей ребенка.

Итак, взаимосвязь математических и познавательных спо­собностей выглядит следующим образом (схема 2).

¹ Пиаже Ж. Генезис числа у ребенка. Женева, 1941.

Математические познавательные способности

Сенсорные

(восприятие: форма, размер, количество, пространственное расположение)

Интеллектуальные

(мышление: сравнение, обобщение, анализ, синтез, классифика­ция, абстрагирование и др.)

Внимание, память, воображение (условия успешности)

Итак, суть вопроса организации внешних условий развити математических способностей ребенка возвращает нас к про блеме отбора адекватного математического содержания для занятий с детьми дошкольного возраста. Чем младше ребенок, тем больше необходимость того, чтобы он мог получать инфор­мацию об изучаемых объектах и их отношениях непосредст­венно через сенсорные каналы, причем наиболее важны в воз­расте до 6-7 лет руки и глаза. Не случайно все, что воспитатель приносит на занятие, ребенок стремится хотя бы потрогать, а лучше — получить в собственные руки для манипулирова­ния. Оптимальным для такого манипулирования является гео­метрический материал.

Количественная характеристика является опосредованной, для ее восприятия надо быть подготовленным к пониманию того, что эта характеристика есть и что она, как правило, не зависит от других свойств и качеств предмета (у мухи ног больше, чем у слона; а в Попугаях Удав не длиннее, чем в Мар­тышках, хотя Попугаев — 38, а Мартышек — 3). Иными сло­вами, количественные характеристики объектов и явлений (и тем более отношения между ними) не являются восприни­маемыми ребенком непосредственно, а требуют специального предварительного обучения для адекватного восприятия и ос­мысления.

В предыдущей лекции мы уже останавливались на вопро­сах специфики математических характеристик предметов и яв­лений, на вопросах специфики математической символики. Сложность этих понятий часто не осознается даже воспитате­лями-практиками. Например, на вопрос, можно ли дать ребен­ку в руки число или показать детям число на занятии, часто можно услышать: «Да, можно». На вопрос: «Что именно вы покажете, знакомя ребенка с числом два? » — воспитатели час­то отвечают: «Цифру 2» или «Два кубика» и т. п. Эти ответы показывают, что даже взрослый человек не всегда дифферен­цирует такие элементарные математические понятия, как чис­ло, цифра и множество. Правильное восприятие и адекватное понимание этих понятий требует предварительного специаль­ного обучения ребенка, однако это не означает, что нельзя зани­маться математическим развитием малыша. Геометрический материал является полноценным математическим материа­лом, просто он менее привычен для традиционного восприятия взрослого в содержании обучения дошкольника, чем арифме­тический. С психологической и методической точки зрения геометрический материал намного удобнее при обучении до­школьника, поскольку воспринимаем сенсорикой и легко под­дается наглядному (вещественному и графическому) моде­лированию. При этом любой геометрический объект имеет количественные характеристики, как воспринимаемые при минимальной подготовке ребенка (количество сторон, углов), так и позволяющие многократно возвращаться к анализу этих объектов с целью выявления новых численных характеристик (в дальнейшем в школе ребенок познакомится со способами из­мерения длин сторон и градусной мерой углов, способами вычислений периметров и площадей и т. д.). Например, в рас­смотренном выше фрагменте занятия любая конструкция (кон­структивная ситуация) имела количественную характеристи­ку, но не требовала символизации (цифрового обозначения), хотя и могла ею сопровождаться. Этот же фрагмент занятия в символьном сопровождении мог бы быть предложен для про­ведения в старшей и даже подготовительной группе (естест­венно, при некоторой модернизации и усложнении содержа­ния упражнений). Как видим, речь не идет о полном отказе от работы с количественными характеристиками объектов и от­ношений между ними, речь идет об изменении иерархии этой работы в соответствии с принципом природосообразности (т. е.в соответствии с психологическими особенностями усвоени детьми математических понятий), а также в соответствии с ди­дактическими принципами организации развивающего обу­чения.

Таким образом, перестроение методологической базы мате­матического развития дошкольников на основе использования моделирования как ведущего способа и средства изучения математических понятий и отношений между ними требует оп­ределенного смещения акцентов в отборе и выстраивании содержательной основы этого процесса.

Глава 2

ОСНОВНЫЕ ПОНЯТИЯ КУРСА МАТЕМАТИКИ ДЛЯ ДОШКОЛЬНИКОВ И ОСОБЕННОСТИ ИХ ФОРМИРОВАНИЯ С ТОЧКИ ЗРЕНИЯ ПРЕЕМСТВЕННЫХ РАЗВИВАЮЩИХ ТЕХНОЛОГИЙ

Лекция 7