Глава 1. Дидактические и психофизиологические основыматематического развития дошкольников

Белошистая А. В.

Б43 Формирование и развитие математических способно­стей дошкольников: Вопросы теории и практики: Курс лек­ций для студ. дошк. факультетов высш. учеб. заведений. — М.: Гуманит. изд. центр ВЛАДОС, 2003. — 400 с: ил.

Издание представляет собой курс лекций, в которых рассматри­ваются вопросы формирования и развития математических способ­ностей дошкольников. Пособие отражает современное понимание преемственности математического образования дошкольников и младших школьников, возможности формирования компонентов учебной деятельности и развития познавательных процессов дошко­льников. В нем освещены принципы отбора содержания курса дошкольной математической подготовки, вопросы методического анализа занятий и программ по математике, организации индиви­дуального подхода к ребенку при обучении математике.

В пособие включены вопросы частной методики формирования элементарных математических представлений дошкольников с по­зиций развивающего обучения, а также опыт организации соответ­ствующих занятий.

УДК 373.2.016:51(075.8) ББК 74.102я73

ОГЛАВЛЕНИЕ

Предисловие..............................................................................................................

Глава 1. Дидактические и психофизиологические основыматематического развития дошкольников

Лекция 1. О цели предматематической подготовкидошкольников в русле идей развивающегообучения

Лекция 2. Преемственность между дошкольными начальным звеньями системы образования

Лекция 3. Формирование преемственных компонентовучебной деятельности дошкольникаи младшего школьника

Лекция 4. Обучение как целенаправленный процессв дошкольном образовательном учреждении

Лекция 5. Психологические основы методическойконцепции математического развития
ребенка дошкольного возраста

Лекция 6. Взаимосвязь развития познавательныхпроцессов и математических способностей
дошкольников

Глава 2. Основные понятия курса математики для дошкольников и особенности их формирования с точки зренияпреемственных развивающих технологий

Лекция 7. Принципы отбора содержания курса«Математическое развитие дошкольников»

Лекция 8. Знакомство дошкольников с некоторыми понятиями нумерации целыхнеотрицательных чисел

Лекция 9. Методика знакомства дошкольниковс двузначными числами

Лекция 10. Знакомство дошкольниковс арифметическими действиями сложенияи вычитания

Лекция 11. Подготовка дошкольников к обучениюрешению задач

.Лекции 12. Знакомство дошкольников с величинами

Лекция 13. Знакомство дошкольниковс геометрическими понятиями

Глава 3. Развитие основных компонентов математическогомышления дошкольников

Лекция 14. Формирование и развитие конструктивногомышления как средство развитияпространственного мышленияи математических способностейдошкольника

Лекция 15. Формирование и развитие логическойсферы дошкольника

Глава 4. Профессиональная подготовка воспитателяк проведению занятия по математике

Лекция 16. Подготовка педагога к проведению занятия и планирование курса математического

развития в ДОУ

Лекция 17. Методический анализ занятияпо математике

Глава 5. Реализация принципов личностно-ориентированного обучения в процессе математического развитияребенка дошкольного возраста

Лекция 18. Индивидуальная работа с ребенкомкак основа развития его личности

Лекция 19. Работа со способными к математикедошкольниками как методическая проблема

Лекция 20. Функции диагностики в дошкольномматематическом образовании

Лекция 21. Математика как средство коррекциинедостатков развития ребенкадошкольного возраста

Литература

ПРЕДИСЛОВИЕ

Необходимость систематической подготовки детей в дошко­льных учреждениях к усвоению школьного курса математики явилась причиной введения обязательного курса «Формирова­ние элементарных математических представлений дошкольни­ков» в систему подготовки будущих педагогов-воспитателей дошкольных образовательных учреждений (ДОУ). Традицион­ная методика формирования элементарных математических представлений у детей, созданная А.М. Леушиной¹ и реализо­ванная в пособии Л.С. Метлиной², а затем дополненная автор­ским коллективом под руководством А. А. Столяра³, была разра­ботана в соответствии с типовой программой воспитания и обучения ребенка в детском саду.

1 См.: Леушина А.М. Формирование элементарных математических представлений у детей дошкольного возраста. М., 1974. 2 См.: Метлина Л.С. Занятия по математике в детском саду. М., 1985. 3 См.: Формирование элементарных математических представлений у дошкольников / Под ред. А.А. Столяра. М., 1988.

Учебное пособие А.М. Леушиной имело целью подготовить педагога к обучению детей первоначальным математическим знаниям и умениям, к пониманию математических взаимосвя­зей и взаимозависимостей, к формированию простейших мате­матических понятий. Основной целью этого обучения являлась подготовка дошкольника к школьному обучению. «Работа по формированию у дошкольников элементарных математиче­ских представлений — важнейшая часть их общей подготовки к школе. В связи с переходом к обучению детей с шести лет внимание к этой работе должно быть усилено. Она начинается со второй младшей группы... Воспитатель заботится и о проч­ном усвоении детьми знаний, предусмотренных програм­мой, и, что особенно важно, о развитии у них интересак математическим знаниям, самостоятельности и гибкости мышления, смекалки и сообразительности, умения делать про­стейшие обобщения, доказывать правильность тех или иных суждений. Дети учатся кратко и точно отвечать на вопросы, делать выводы, пользоваться грамматически правильными оборотами речи»¹.

Учебное пособие под редакцией А. А. Столяра имело целью углубление теоретической математической подготовки воспи­тателя. «Педагог должен знать, не только как обучать дошко­льников, но и то, чему он их обучает, т. е. ему должна быть ясна математическая сущность тех представлений, которые он формирует у детей»². Основной целью методики формирова­ния элементарных математических представлений являлась «помощь в подготовке детей дошкольного возраста к воспри­ятию и усвоению математики — одного из важнейших учеб­ных предметов в школе»³.

Необходимость в разработке новых учебных пособий для студентов факультета дошкольной педагогики и педагогов — воспитателей по проблеме обучения дошкольников математи­ке обусловлена принципиальными изменениями в подходах к воспитанию и обучению ребенка в ДОУ, происходящих как в теории, так и в практике работы воспитателя в современных условиях. В настоящее время в «Концепции содержания непрерывного образования (дошкольное и начальное звено)» отмечается, что характерной чертой системы дошкольного об­разования является широкое распространение вариативных программ, целью которых является реализация идей разви­вающего обучения.

1 Метлина Л.С. Указ. изд. С. 3. 2 Формирование элементарных математических представлений... Указ. изд. С. 3. 3 Там же. С. 4.

При этом как выбор вариативной образовательной програм­мы, так и задача ее реализации в русле идей развивающего обучения возлагаются непосредственно на воспитателя. В этой связи в «Концепции...» отмечается, что «происходящие в системе образования изменения показали неготовность зна­чительной части педагогических кадров к осознанному выбо­ру вариативной образовательной программы и ее адекватной реализации с учетом возможностей и потребностей детей».

Данная ситуация закономерна, поскольку в свое время бу­дущие воспитатели прошли целенаправленную подготовку к работе по типовой программе обучения и воспитания ребен­ка в детском саду.

Появление вариативных образовательных программ, значи­тельно отличающихся от типовой программы как содержатель­но, так и концептуально, потребовало от воспитателя умения ра­ботать с новым, непривычным содержанием (часто не входящим в объем математической подготовки воспитателя в вузе и пед­училище), а также знания современных развивающих методик обучения математике в применении к дошкольному возрасту.

Главной целью подготовки педагога на современном этапе являются формирование и развитие у педагога творческого методического мышления, формирование самостоятельной аналитической деятельности, позволяющей провести теоре­тический анализ при выборе адекватной альтернативной про­граммы в соответствии с учетом возможностей и потребностей своих детей, а также методологический анализ программы и ее дидактического обеспечения.

Не менее важной задачей является совершенствование зна­ний педагога об общих способах методической деятельности, которыми он может пользоваться при организации изучения различных математических понятий детьми дошкольного воз­раста, и знаний о специфике использования различных разви­вающих технологий при обучении математике дошкольников.

Данное пособие имеет целью познакомить студентов фа­культета дошкольной педагогики и психологии с возможными способами решения тех методологических задач, с которыми они неизбежно столкнутся в процессе практической работы по освоению различных уже имеющихся и тех, что будут появ­ляться в дальнейшем, альтернативных программ дошкольно­го образования.

Так, в тексте «Концепции...» обозначено: «...серьезной проблемой является игнорирование создателями программ и учебных пособий закономерностей психического развития ребенка — сензитивности разных возрастных периодов к ста­новлению тех или иных психических функций и новообразо­ваний, роли ведущей деятельности в их формировании». В свя­зи с этим значительное место в пособии отведено обоснованию концепции математического развития ребенка дошкольного возраста.

За отправное положение данной концепции принята мысль о том, что целью дошкольной математической подготовки долж­но, главным образом, являться формирование и развитие мате­матических способностей ребенка дошкольного возраста. Этот вопрос в традиционной методике формирования элементарных математических представлений является дискуссионным. Дале­ко не все педагоги сегодня считают необходимым реализовывать развивающее обучение уже на дошкольном этапе работы с ре­бенком. Целью же развивающего обучения является не столько формирование у ребенка определенного списка знаний, умений и навыков предметного характера, сколько развитие высших психических функций, его способностей и раскрытие внутрен­него потенциала ребенка.

Нам представляется полезным познакомить студентов с не­которыми наиболее разработанными областями теории и прак­тики математического развития ребенка младшего возраста, а также с опытом практической реализации рассмотренных теоретических идей.

Методика математического образования — развивающая­ся наука, особенно бурным является ее прогресс в последние десятилетия, поэтому педагог должен уметь анализировать и осознавать свой опыт и необходимость его совершенствова­ния в соответствии с обогащением науки и практики новыми теориями и методическими разработками.

Автор не ставил задачу дать исчерпывающую детальную ха­рактеристику той или иной методической проблеме с точки зре­ния классической методики обучения математике детей млад­шего возраста.

Существуют крайне разнородные взгляды не только на са­му концепцию математического развития ребенка младшего возраста, но и на возможность построения этой концепции, на само понятие «математические способности», а также на про­блему взаимоотношений теории и практики в образовательном процессе.

Один из возможных вариантов построения методической концепции математического развития ребенка — на основе имеющихся теоретических психологических концепций раз­вивающего обучения — представлен в данном пособии.

Автор считает чрезвычайно важным очертить наиболее существенные аспекты поднятых проблем и вопросов с пози­ции развивающего обучения и личностно-деятельностногопреемственного подхода к построению образовательного про­цесса в ДОУ.

Предлагаемое пособие будет содействовать улучшению ка­чества методической подготовки студентов факультета до­школьной педагогики и психологии к осуществлению матема­тического развития ребенка.

Пособие может быть использовано также преподавателями и слушателями ФПК и ИПК в их совместной работе по повыше­нию качества профессиональной подготовки воспитателя ДОУ.

Лекция 1

О ЦЕЛИ ПРЕДМАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ ДОШКОЛЬНИКОВ В РУСЛЕ ИДЕЙ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ

1. Математические знания в современном мире.

2. О цели предматематической подготовки ребенка с пси­хологической точки зрения.

3. Традиционное математическое образование в ДОУ.

4. О приоритетных целях дошкольного образования в конце XX и начале XXI в.

Лекция 2

ПРЕЕМСТВЕННОСТЬ МЕЖДУ ДОШКОЛЬНЫМ И НАЧАЛЬНЫМ ЗВЕНЬЯМИ СИСТЕМЫ ОБРАЗОВАНИЯ

1. Четырехлетнее обучение и кризис седьмого года жизни.

2. Преемственность как одно из условий непрерывного об­разования ребенка.

3. О построении системы взаимосвязанных образователь­ных звеньев.

4. О категории «готовность к школе» с педагогической и пси­хологической точки зрения.

Лекция 4

ОБУЧЕНИЕ КАК ЦЕЛЕНАПРАВЛЕННЫЙ ПРОЦЕСС В ДОШКОЛЬНОМ ОБРАЗОВАТЕЛЬНОМ УЧРЕЖДЕНИИ

1. Образовательный процесс как процесс, ведущий разви­тие дошкольника.

2. Об образовательных программах.

3. Что результативнее при организации обучения: целевая направленность или свободная деятельность детей?

4. К вопросу о теоретическом обосновании построения про­цесса обучения на дошкольном этапе.

Рассмотрим современные взгляды на пути и способы орга­низации образовательного процесса в ДОУ с целью реализации идей развивающего обучения.

Образовательный процесс как процесс, ведущий развитие дошкольника

Приведем еще три определения понятий, имеющих важное значение для понимания сути организации образовательного процесса¹.

¹ Усова АЛ. Указ. изд. С. 168

Научение — процесс и результат приобретения индивиду­ального опыта.

Обучение — процесс целенаправленной передачи общест­венно-исторического опыта; организация формирования зна­ний, умений и навыков.

Развивающее обучение — обучение, которое ведет к фор­мированию все более и более внутренне расчлененных и иерар­хически упорядоченных когнитивных структур, к образова­нию все новых и новых элементов и увеличению связей между ними. (Под когнитивными структурами понимают структуры, определяющие творческое мышление индивида.)

Результатом научения является усвоение, в то же время ус­воение есть форма психического развития маленького ребен­ка. «Психическое развитие детей, — пишет Д.Б. Эльконин, — происходит в форме усвоения. Все то, что появляется у детей в ходе их психического развития, в «идеальной» форме дано им в социальной действительности как источнике развития и может стать их достоянием только через усвоение»².

Таким образом, обучение можно рассматривать как процесс, ведущий развитие ребенка младшего возраста.

1 Шаграева ОМ. Указ. изд. С. 277. 2 Эльконин Д.Б. О структуре учебной деятельности // Избр. психоло­гические труды. М., 1989. С. 212. 3 Обухова Л.Ф. Детская психология: теория, факты, проблемы. М., 1995. С. 250.

«Вне обучения, вне процесса передачи ребенку обществен­но выработанных способов действий вообще невозможно раз­витие, — отмечает Л.Ф. Обухова. — Обучение в ранних воз­растах вплетено во все виды деятельности ребенка. К концу дошкольного возраста ребенок переходит от спонтанного типа обучения к реактивному типу обучения по программе, пред­ложенной взрослым человеком, и очень важно сделать так, что­бы ребенок захотел сделать то, что хочет взрослый»³.

Таким образом, обучение должно носить организованный характер, причем функцию организации этого процесса выпол­няет взрослый.

В целях планомерного и систематического влияния воспи­тателя на детей в группе обучение в детском саду строится как организованный процесс и протекает в форме занятий с груп­пой детей определенного возраста. Опыт работы детских садов более чем вековой истории показал необходимость создания программ обучения и достаточно убедительно раскрыл то, что целый ряд весьма существенных новообразований в психиче­ской и познавательной сфере ребенка-дошкольника (не говоря уже о знаниях и умениях) активно формируются у детей, по­сещающих детский сад, в результате целенаправленной рабо­ты педагога на занятиях.

2. Об образовательных программах

Сегодня по-прежнему актуальна проблема исследования оп­тимальных границ образовательного содержания программ для различных возрастов. Именно этим можно объяснить соз­дание альтернативных программ, которые весьма значитель­но отличаются друг от друга в содержательном плане. Програм­ма обучения в классическом понимании должна содержать точно очерченный круг знаний и умений, которыми должны овладеть все дети в группе в результате учебных занятий в дет­ском саду. Именно в этом и кроется противоречие, разрешить которое пока не удается, поскольку расширение обязательно­го перечня в программе может привести к недоступности этой программы для большинства детей; резкое сужение этого пе­речня — к искусственному сдерживанию потенциала детей; а модная сейчас «уровневость» в перечне обязательных зна­ний и умений позволяет педагогу «кивать» на «недостаточный уровень природных способностей ребенка» и ориентировать­ся на то, что ребенок сам «возьмет», сколько может (принцип «мини-макса»). Такая позиция, на наш взгляд, в корне расхо­дится с концепцией развивающей роли обучения в жизни ре­бенка, поскольку предполагает приспособление ребенка к про­грамме, а не программы и методологии к ребенку (принцип природосообразности). Естественно, что второй подход подни­мает еще одну глобальную проблему современной теории обучения — проблему разработки методологического обес­печения содержательной части программы. На наш взгляд, решение этой проблемы возможно только при учете иерар­хических взаимосвязей этого триединства: ребенок — мето­дология — содержание. Попытки решить ее, исходя из ана­лиза двух звеньев: ребенок (психологические особенности) и содержание (понятия и способы действий с ними), как раз и приводят к «уровневому» подходу в анализе результатив­ности программы: кто смог -«взял», кто не смог — «не взял»; значит, у одного уровень обучаемости высокий, а у другого низкий; и если мы будем в своей деятельности ориентиро­ваться на эти уровни как исходные, то возникает законный вопрос: где же при этом развивающая и формирующая роль педагога?

Перспективы дальнейшей работы над программой обучения в детском саду прекрасно определяются мыслью Л.С. Выгот­ского, звучащей вполне современно: «Если задаться вопросом, каким требованиям должна удовлетворять программа детско­го сада для того, чтобы она была приведена в соответствие с особенностями ребенка дошкольного возраста, то ответ на него, мне кажется, будет звучать так. Эта программа должна обладать следующими двумя трудно соединимыми качества­ми. Во-первых, она должна быть построена по какой-то систе­ме, которая ведет ребенка к определенной цели, каждый год делая определенные шаги по пути движения к этой цели. Эта программа должна быть сходной со школьной программой в том смысле, что она должна быть программой единого систе­матического цикла общеобразовательной работы. Вместе с тем эта программа должна быть и программой последовательно­сти, которая отвечает эмоциональным интересам ребенка и особенностям его мышления...»¹.

1 Выготский Л.С. Обучение и развитие в дошкольном возрасте // Умет венное развитие детей в процессе обучения. М., 1935. С. 20.

То, что эта цитата абсолютно адекватна требованиям к про­грамме математического образования дошкольника, являет­ся неоспоримым положением. Однако то, что это положение систематически нарушается авторами различных программ математического образования, — явление столь же очевидное. Сегодня, как и в предыдущее столетие, содержание математи­ческого образования дошкольников определяется отнюдь не в соответствии с приведенным выше положением, а либо в со­ответствии с традицией формирования этого содержания, сло­жившейся еще во времена Фребеля и Лая¹ и определяющей цели математического образования ребенка как обучение счету и действиям с числами, либо в соответствии с диктатом про­граммы следующего образовательного звена — начальной школы и необходимостью подготовить ребенка к изучению значительно расширенного и усложненного математического содержания.

Лекция 5

Лекция 6

Упражнение 1

Цель. Подготовить детей к последующей моделирующей деятельно­сти посредством простых конструктивных действий, актуализировать счетные умения, организовать внимание.

Материалы. Счетные палочки двух цветов, фланелеграф с картонны­ми моделями палочек у педагога.

Задание.

— Возьмите из коробки столько палочек, сколько у меня. Положите пе­ред собой так же (II). Сколько палочек? {Две.)

— У кого палочки одного цвета? У кого разного цвета? Какого цвета у тебя палочки? (Одна — красная, одна — зеленая.)

— Один да один. Сколько вместе? (Два.)

Упражнение 2

Цель. Организовать конструктивную деятельность по образцу, упраж­нять в счете, развитие воображения, речевой деятельности. Материалы. Счетные палочки, фланелеграф. Задание.

— Возьмите еще одну палочку и положите ее сверху (II). Сколько ста­ло палочек? Сосчитаем. (Три.)

— На что похожа фигура? (На ворота, на букву П). Кто знает слова, начинающиеся на П?

Дети говорят слова.

Упражнение 3

Цель. Развивать наблюдательность, воображение и речевую деятель­ность; формировать умение оценивать количественную характеристику видоизменяющейся конструкции (без изменения количества элементов); подготовка к правильному восприятию смысла арифметических действий.

Материалы. Счетные палочки, фланелеграф.

Задание.

— Верхнюю палочку переложите так: "Н Изменилось ли количество палочек? Почему не изменилось? (Палочку переставили, но не убрали и не добавили.)

— На что теперь похожа фигура? (На букву Н.) Назовите слова, начинаю­щиеся на Н.

Упражнение 4

Цель. Формировать конструкторские умения, воображение, память и внимание.

Задание.

— Сложить из этих трех палочек разные фигурки.

Дети складывают фигурки и буквы. Называют их, придумывают слова. Кто-нибудь из детей обязательно сложит треугольник.

Упражнение 5

Цель. Формировать образ треугольника, первичное обследование мо­дели треугольника.

Материалы. Счетные палочки, фланелеграф.

Способ выполнения. Педагог предлагает всем сложить такую фигуру:А

— Сколько палочек вам понадобилось для этой фигуры? (Три.) Кто знает, что это? (Треугольник.) Кто знает, почему он так называется? (Три угла.)

Если дети не могут назвать фигуру, педагог подсказывает ее название и просит детей объяснить, как они его понимают.

Педагог просит обвести фигуру пальцем, сосчитать углы (вершины), касаясь их пальцем.

Упражнение 6

Цель. Закреплять образ треугольника на кинестезическом и визуаль­ном уровне. Распознавать треугольник среди других фигур (объем и ус­тойчивость восприятия). Обводить и штриховать треугольники (развивать мелкие мышцы руки).

Материалы. Рамка-трафарет с прорезями в форме геометрических фи­гур, бумага, карандаши.

Примечание. Задание является проблемным, поскольку на исполь­зуемой рамке есть несколько треугольников и фигур, на них похожих ост­рыми углами (ромб, трапеция).

Задание.

— Найдите на рамке треугольник. Обведите его. Заштрихуйте треуголь­ник по рамке. (Штриховка производится внутри рамки, кисть движется сво­бодно, карандаш «стучит» по рамке.)

Упражнение 7

Цель. Закреплять визуальный образ треугольника. Распознавать нуж­ные треугольники среди других треугольников (точность восприятия). Раз­вивать воображение и внимание, мелкую моторику.

Материалы. Трафарет, бумага, карандаши.

Задание.

— Посмотрите на этот рисунок: Кошка-мама, кот-папа и котенок, каких фигур они составлены? (Круги и треугольники.)

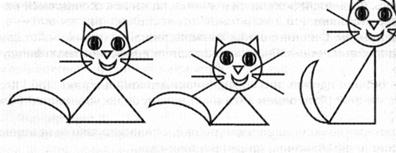
— Кто нарисовал такой треугольник, какой нужен для котенка? Для кош­ки-мамы? Для кота-папы? Дорисуйте своего кота.

Дети дорисовывают, используя тот треугольник, который у них есть, т. е. у каждого получается свой кот. Затем они дорисовывают остальных кошек, ориентируясь на образец, но самостоятельно.

Педагог обращает внимание на то, что кот-папа самый высокий.

— Правильно поставьте рамку, чтобы кот-папа получился самый вы­сокий.

Данное упражнение не только способствует накоплению у ребенка за­пасов образов геометрических фигур, но и развивает его пространст­венное мышление, поскольку фигуры на рамке расположены в различных положениях и, чтобы найти нужную, необходимо узнать ее в другой пози­ции, а затем повернуть рамку для ее рисования в такой позиции, которую требует рисунок.

Приведенные фрагменты занятий показывают способ по­строения взаимосвязанной системы заданий для формирова­ния и развития сенсорных познавательных способностей на математическом материале. Очевидно, что деятельность ре­бенка в данном фрагменте является также организующей его внимание и стимулирующей воображение.

Перейдем к другой группе познавательных способностей — к интеллектуальным способностям. Как уже было сказано, в их основе лежит развитое мышление. Процесс развитиямышления методически состоит в формировании и развитии обобщенных приемов умственных действий (сравнение, обоб­щение, анализ, синтез, сериация, классификация, абстра-гирование, аналогия и др.), что является общим условием функционирования самого мышления как процесса в любой области познания, в том числе и в математике. Безусловным является то, что сформированность умственных действий яв­ляется абсолютной необходимостью для развития матема­тического мышления, не случайно эти умственные действия именуются также приемами логических умственных дейст­вий. Их формирование стимулирует развитие математических способностей ребенка. Одним из самых значительных иссле­дований в этой области явилась работа швейцарского психо­лога Ж. Пиаже «Генезис числа у ребенка»¹, в которой автор достаточно убедительно доказывает, что формирование поня­тия числа (а также и арифметических операций) у ребенка кор­релятивно развитию самой логики: формированию логических структур, в частности формированию иерархии логических классов, т. е. классификации, и формированию асимметрич­ных отношений, т. е. качественных сериаций. Классификация и сериация являются приемами умственных действий, форми­рование которых невозможно без предварительного развития у ребенка операций сравнения, обобщения, анализа и синте­за, абстрагирования, аналогии и систематизации.

Легко показать на приведенном выше фрагменте занятия, что каждое из приведенных упражнений одновременно «работает» также на формирование всех этих мыслительных приемов. На­пример, упражнение 1 учит ребенка сравнивать; упражнение 2 — сравнивать и обобщать, а также анализировать; упражнение 3 учит анализу и сравнению; упражнение 4 — синтезу; упражне­ние 5 — анализу, синтезу и обобщению; упражнение б — фак­тическая классификация по признаку; упражнение 7 учит срав­нению, синтезу и элементарной сериаций.

Таким образом, математическое содержание оптимально для развития всех познавательных способностей (как сенсор­ных, так и интеллектуальных), приводит к активному разви­тию математических способностей ребенка.

Итак, взаимосвязь математических и познавательных спо­собностей выглядит следующим образом (схема 2).

¹ Пиаже Ж. Генезис числа у ребенка. Женева, 1941.

Математические познавательные способности

Сенсорные

(восприятие: форма, размер, количество, пространственное расположение)

Интеллектуальные

(мышление: сравнение, обобщение, анализ, синтез, классифика­ция, абстрагирование и др.)

Внимание, память, воображение (условия успешности)

Итак, суть вопроса организации внешних условий развити математических способностей ребенка возвращает нас к про блеме отбора адекватного математического содержания для занятий с детьми дошкольного возраста. Чем младше ребенок, тем больше необходимость того, чтобы он мог получать инфор­мацию об изучаемых объектах и их отношениях непосредст­венно через сенсорные каналы, причем наиболее важны в воз­расте до 6-7 лет руки и глаза. Не случайно все, что воспитатель приносит на занятие, ребенок стремится хотя бы потрогать, а лучше — получить в собственные руки для манипулирова­ния. Оптимальным для такого манипулирования является гео­метрический материал.

Количественная характеристика является опосредованной, для ее восприятия надо быть подготовленным к пониманию того, что эта характеристика есть и что она, как правило, не зависит от других свойств и качеств предмета (у мухи ног больше, чем у слона; а в Попугаях Удав не длиннее, чем в Мар­тышках, хотя Попугаев — 38, а Мартышек — 3). Иными сло­вами, количественные характеристики объектов и явлений (и тем более отношения между ними) не являются восприни­маемыми ребенком непосредственно, а требуют специального предварительного обучения для адекватного восприятия и ос­мысления.

В предыдущей лекции мы уже останавливались на вопро­сах специфики математических характеристик предметов и яв­лений, на вопросах специфики математической символики. Сложность этих понятий часто не осознается даже воспитате­лями-практиками. Например, на вопрос, можно ли дать ребен­ку в руки число или показать детям число на занятии, часто можно услышать: «Да, можно». На вопрос: «Что именно вы покажете, знакомя ребенка с числом два? » — воспитатели час­то отвечают: «Цифру 2» или «Два кубика» и т. п. Эти ответы показывают, что даже взрослый человек не всегда дифферен­цирует такие элементарные математические понятия, как чис­ло, цифра и множество. Правильное восприятие и адекватное понимание этих понятий требует предварительного специаль­ного обучения ребенка, однако это не означает, что нельзя зани­маться математическим развитием малыша. Геометрический материал является полноценным математическим материа­лом, просто он менее привычен для традиционного восприятия взрослого в содержании обучения дошкольника, чем арифме­тический. С психологической и методической точки зрения геометрический материал намного удобнее при обучении до­школьника, поскольку воспринимаем сенсорикой и легко под­дается наглядному (вещественному и графическому) моде­лированию. При этом любой геометрический объект имеет количественные характеристики, как воспринимаемые при минимальной подготовке ребенка (количество сторон, углов), так и позволяющие многократно возвращаться к анализу этих объектов с целью выявления новых численных характеристик (в дальнейшем в школе ребенок познакомится со способами из­мерения длин сторон и градусной мерой углов, способами вычислений периметров и площадей и т. д.). Например, в рас­смотренном выше фрагменте занятия любая конструкция (кон­структивная ситуация) имела количественную характеристи­ку, но не требовала символизации (цифрового обозначения), хотя и могла ею сопровождаться. Этот же фрагмент занятия в символьном сопровождении мог бы быть предложен для про­ведения в старшей и даже подготовительной группе (естест­венно, при некоторой модернизации и усложнении содержа­ния упражнений). Как видим, речь не идет о полном отказе от работы с количественными характеристиками объектов и от­ношений между ними, речь идет об изменении иерархии этой работы в соответствии с принципом природосообразности (т. е.в соответствии с психологическими особенностями усвоени детьми математических понятий), а также в соответствии с ди­дактическими принципами организации развивающего обу­чения.

Таким образом, перестроение методологической базы мате­матического развития дошкольников на основе использования моделирования как ведущего способа и средства изучения математических понятий и отношений между ними требует оп­ределенного смещения акцентов в отборе и выстраивании содержательной основы этого процесса.

Глава 2

ОСНОВНЫЕ ПОНЯТИЯ КУРСА МАТЕМАТИКИ ДЛЯ ДОШКОЛЬНИКОВ И ОСОБЕННОСТИ ИХ ФОРМИРОВАНИЯ С ТОЧКИ ЗРЕНИЯ ПРЕЕМСТВЕННЫХ РАЗВИВАЮЩИХ ТЕХНОЛОГИЙ

Лекция 7

Постановка проблемы

Вопрос о принципах отбора содержания курса математиче­ского развития дошкольников является традиционным для этой дисциплины. Любая методическая дисциплина отвечает на три основных вопроса:

1. Зачем обучать? — вопрос о целях и задачах обучения.

2. Чему обучать? — вопрос о содержании обучения в соот­ветствии с поставленными задачами.

3. Как обучать? — вопрос о методологии и частных методи­ках обучения конкретным понятиям и способам действий с ними.

Первый вопрос рассматривался в лекции 1. Ответ на тре­тий вопрос мы обсуждали в общем виде в лекции 4.

В этой же лекции постараемся сформулировать ответ на вто­рой вопрос, который предполагает разработку принциповотбора содержания в соответствии с предложенной в данно курсе концепцией математического развития ребенка.

Математика как наука не изучает конкретные предметы ил явления в их непосредственном проявлении. Предметом ее изучения являются только количественные и пространствен­ные характеристики изучаемых объектов, явлений, процессо с помощью специфических математических моделей, имею­щих высокую степень абстрактности и общности. Если челове в состоянии построить какую-либо модель изучаемого предм та, процесса, ситуации, отношений и описать ее на матема­тическом языке, значит, он обладает тем, что можно назватматематическим мышлением.

Очевидно, что задача развития такого вида мышлени должна решаться в процессе обучения математике. Отсюда еле дует, что с первых шагов обучения математике намного важнее так организовать учебный процесс, чтобы ребенок понимал, что математика — это лишь одна из условных моделей мира. Намного важнее учить ребенка определенным моделирующим действиям (умениям), чем конкретным предметным навыкам, так как только в этом случае он сможет впоследствии соз­нательно оперировать абстрактными математическими поня­тиями.

Модель помогает раскрыть смысл вводимых математических понятий посредством их образной подачи, а подключение резер­вов образного мышления к усвоению абстрактных математиче­ских зависимостей существенно облегчает усвоение и запоми­нание учебного материала, разгружает память детей, поскольку образ является более компактной единицей, чем цепочка зна­ковых преобразований или вербальных рассуждений. Психоло­гические исследования показывают, что использование модели­рования как способа и модел