Доверительные интервалы для коэффициентов: реальные статистические данные

Практическому построению доверительных интервалов для коэффициентов a_j нормальной модели линейной множественной регрессии

у=a₀+a₁х₁ +a₂х₂ +…+a_mх_m+e.

где e нормально распределенная случайная величина с параметрами 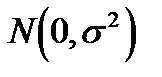, препятствует вхождение в выражения для дисперсий

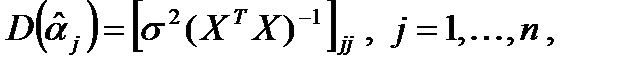
неизвестного значения s².

Единственный выход из этого положения –заменить неизвестное значение s²какой-нибудь подходящей его оценкой (estimate), которую можно было бы вычислить на основании имеющихся статистических данных. Такого рода оценки принято называть статистиками (statistics).

В данной ситуации такой подходящей оценкой для неизвестного значения 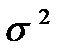является статистика

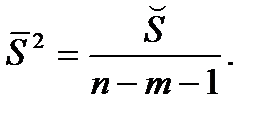(см. (2.8)).

Поскольку сумма 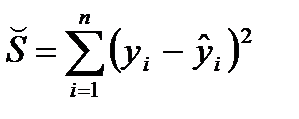является квадратичной функцией от случайных величинe=( 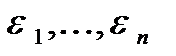), то она является случайной величиной, а следовательно, случайной величиной является и статистика `S².

Математическое ожидание этой случайной величины равно :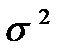

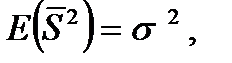
т. е. 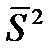–несмещенная оценка для .

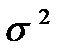Замечание.В частном случае (при отсутствии факторов) модель наблюдений принимает вид

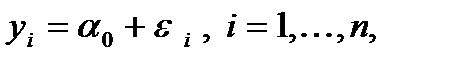
(случайная выборка из распределения N (a₀,s²)). Несмещенной оценкой для 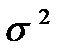служит

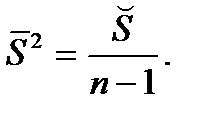
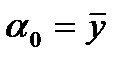Оценкой наименьших квадратов для параметра a₀ является , так что

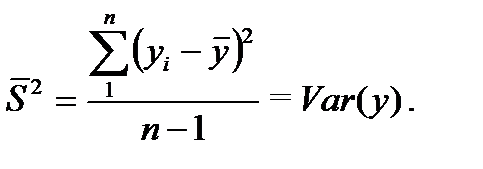
Таким образом, выборочная дисперсия 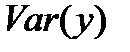переменной 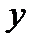, получаемая делением 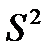именно на 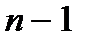(а не на 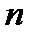), является несмещенной оценкой для 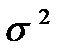в модели случайной выборки из нормального распределения, имеющего дисперсию 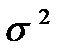. Этим и объясняется сделанный нами выбор нормировки при определении выборочных дисперсий и ковариаций.

При выполнении стандартных предположений отношение

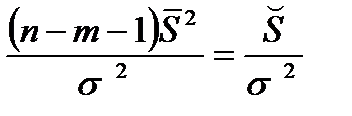
имеет стандартное распределение, называемое распределением хи-квадрат с (n-m-1) степенями свободы. Такое же распределение имеет сумма квадратов 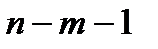случайных величин, независимых в совокупности и имеющих одинаковое стандартное нормальное распределение. При график функции плотности этого распределения имеет вид

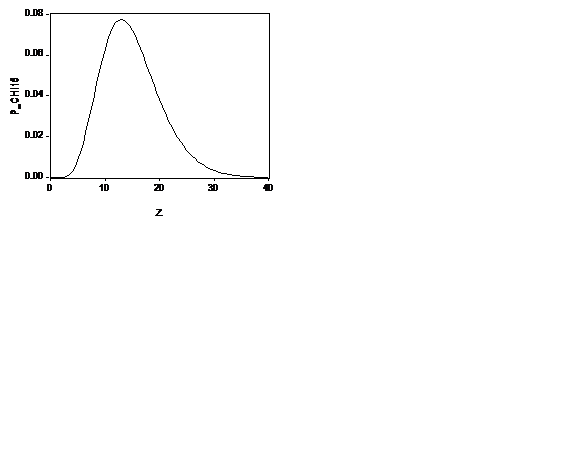
Для обозначения распределения хи-квадрат сKстепенями свободы используют символ c²(K).

Итак, мы не знаем истинного значения 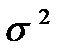и поэтому в попытке построить доверительный интервал для a_j вынуждены заменить неизвестное нам значение 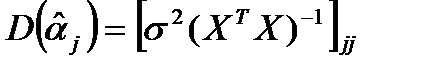на его несмещенную оценку

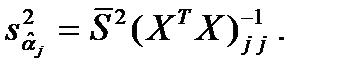
Соответственно, вместо отношения

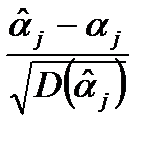
приходится использовать отношение

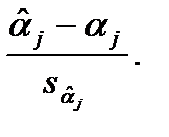
Однако последнее отношение как случайная величина уже не имеет стандартного нормального распределения, поскольку в знаменателе теперь стоит не постоянная, а случайная величина.

Тем не менее, распределение последнего отношения также относят к стандартным, и оно известно под названием t-распределения Стьюдента с (n-m-1) степенями свободы.

Для распределения Стьюдента с Kстепенями свободы принято обозначение t (K). Квантиль уровня ртакого распределения будем обозначать символом t_p(K). График функции плотности распределения Стьюдента симметричен относительно нуля и похож на график функции плотности нормального распределения.

Например, приK=10 он имеет следующий вид (левый график).

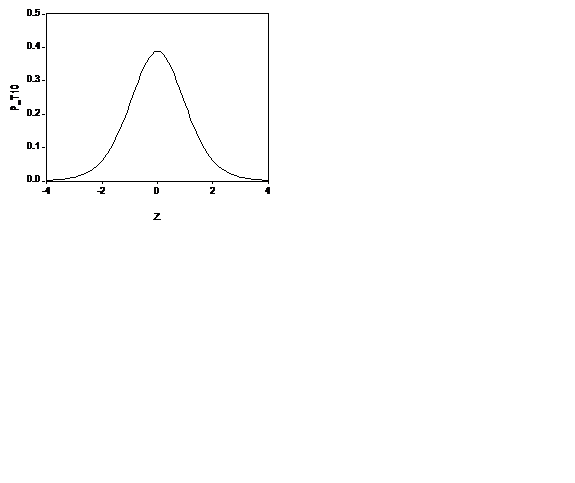
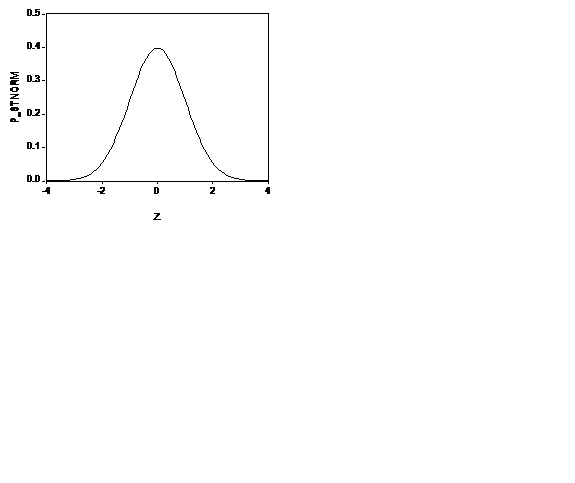
Для сравнения, справа приведен график функции стандартного нормального распределения. Отличие графиков столь невелико, что визуально они почти неразличимы. Квантили этих двух распределений различаются более ощутимо:

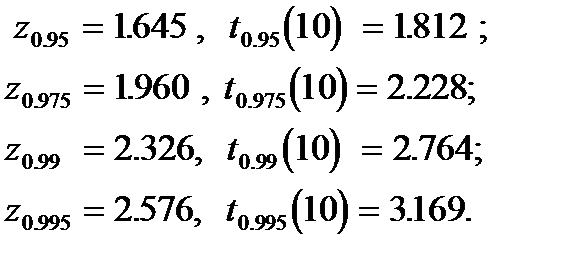
Распределение Стьюдента имеет более тяжелые хвосты. Из приведенных значений квантилей следует, например, что случайная величина, имеющая стандартное нормальное распределение, может превысить значение 1.645 лишь с вероятностью 0.05. В то же самое время, с такой же вероятностью 0.05 случайная величина, имеющая распределение Стьюдента с 10 степенями свободы, принимает значения, большие, чем 1.812.

Впрочем, для значений 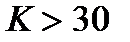квантили распределения Стьюдента 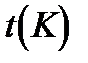практически совпадают с соответствующими квантилями стандартного нормального распределения .

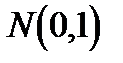Итак,

~ .

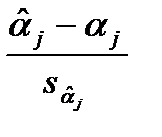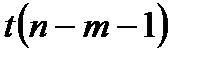Поэтому для этой случайной величины выполняется соотношение

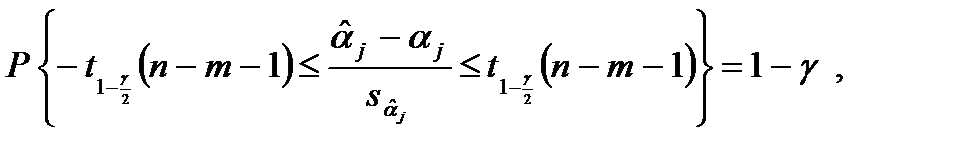
так что с вероятностью, равной 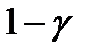, выполняется двойное неравенство

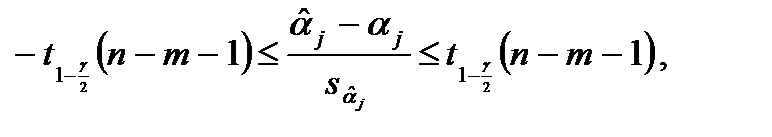
т. е.

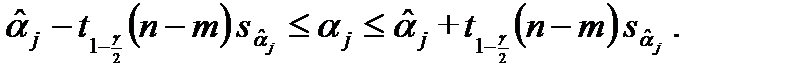
Иными словами, с вероятностью, равной 1-g,случайный интервал

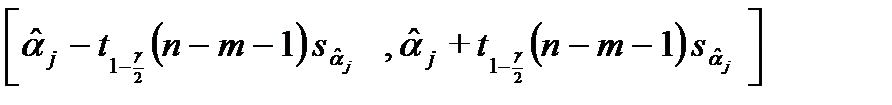
накрывает истинное значение коэффициента α_j, т. е. является 95%- доверительным интервалом для α_jв случае, когда не известно истинное значение s²дисперсии случайных ошибок 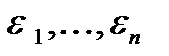. В среднем, длина такого интервала больше, чем длина доверительного интервала с тем же уровнем доверия, построенного при известном значении .

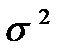Замечание.Выбор конкретного значения 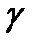определяет компромисс между желанием получить более короткий доверительный интервал и желанием обеспечить более высокий уровень доверия.

Попытка повысить уровень доверия 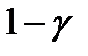, выраженная в выборе меньшего значения 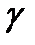, приводит к квантили 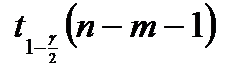с более высоким значением 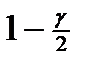, т. е. к большему значению 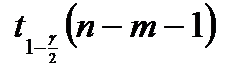. Но длина доверительного интервала пропорциональна 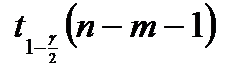. Следовательно, увеличение уровня доверия сопровождается увеличением ширины доверительного интервала(при тех же статистических данных).

Так, для 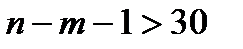можно приближенно считать, что

,

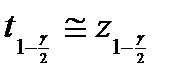где 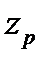– квантиль уровня 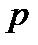стандартного нормального распределения.

Соответственно, выбирая уровень доверия 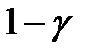равным 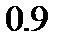, 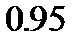или 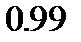, мы получаем для 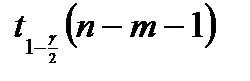значения, приблизительно равные 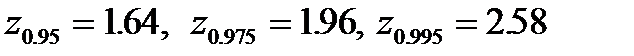. Это означает, что переход от уровня доверия 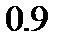к уровню доверия 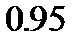сопровождается увеличением длины доверительного интервала приблизительно в 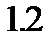раза, а дополнительное повышение уровня доверия до 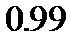увеличивает длину доверительного интервала еще примерно в 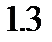раза.

Теперь мы в состоянии перейти к построению интервальных оценок параметров моделей линейной регрессии для различного рода социально-экономических факторов на основании соответствующих статистических данных.

Пример.Пусть при построении модели зависимости уровня безработицы среди белого населения США от уровня безработицы среди цветного населения в виде

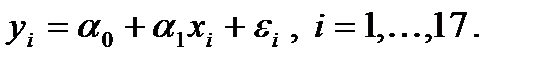
получены следующие значения:

Š=0.161231; .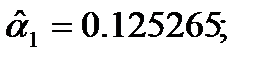

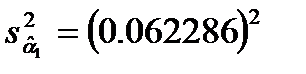Получаем: 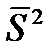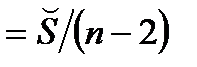= 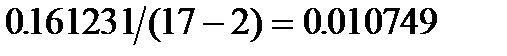. Для построения 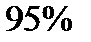— доверительного интервала для 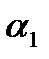остается найти квантиль уровня 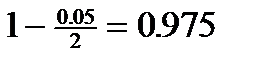распределения Стьюдента с 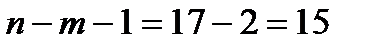степенями свободы. Используя, например, приложение 1, находим: 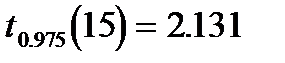. Соответственно, получаем 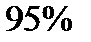-доверительный интервал для 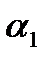в виде

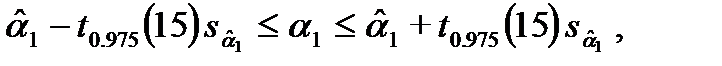
т. е.

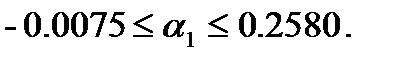
Для 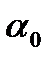имеем 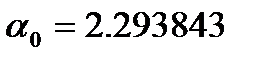, 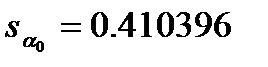; 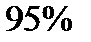-доверительный интервал для 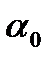имеет вид

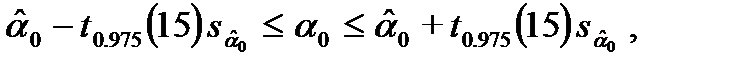
т. е.

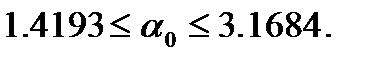
В связи с этим примером, отметим два обстоятельства.

(а) Доверительный интервал для коэффициента 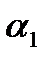допускает как положительные, так и отрицательные значения этого коэффициента.

(б) Каждый из двух построенных интервалов имеет уровень доверия 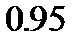; однако это не означает, что с той же вероятностью 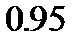сразу оба интервала накрывают истинные значения параметров , .

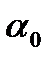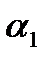Справиться с первым затруднением в данном примере можно, понизив уровень доверия до 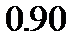. В этом случае в выражении для доверительного интервала квантиль 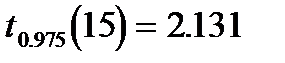заменяется на квантиль 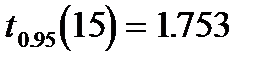, так что левая граница доверительного интервала для 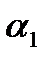становится положительной и равной 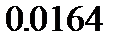. Однако это достигается ценой того, что новый доверительный интервал будет накрывать истинное значение параметра 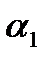в среднем только в 90 случаев из 100, а не в 95 из 100 случаев.

Что касается второго затруднения, то наиболее простой путь взятия под контроль вероятности одновременного накрытия доверительными интервалами для 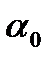, 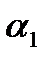истинных значений этих параметров связан с тем, что

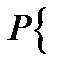оба интервала накрывают 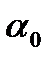и 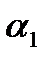, соответственно =

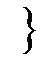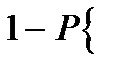хотя бы один из них не накрывает соответствующее =

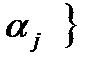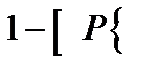доверительный интервал для 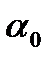не накрывает +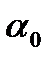

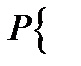доверительный интервал для 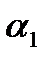не накрывает -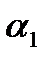

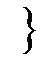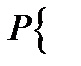оба интервала не накрывают свои =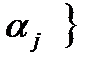

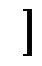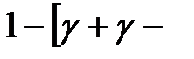
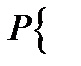оба интервала не накрывают свои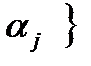 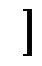³

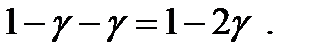
Следовательно, если построить доверительный интервал для 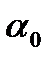и доверительный интервал для 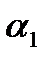с уровнями доверия каждого, равными 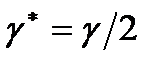, то тогда правая часть полученной цепочки соотношений будет равна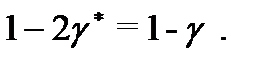

Это означает, что в нашем примере мы можем гарантировать, что вероятность одновременного накрытия истинных значений 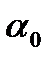, 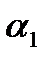соответствующими доверительными интервалами будет не менее 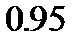, если возьмем 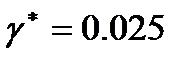. Но тогда при построении этих интервалов придется использовать вместо значения

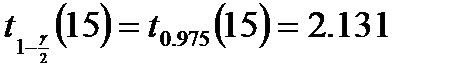
значение

,

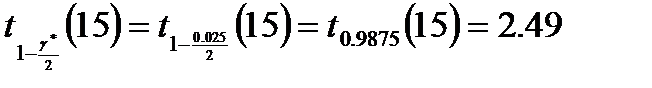так что каждый из исходных интервалов увеличится в 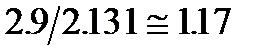раза. Это, конечно, приводит к еще более неопределенным выводам относительно истинных значений параметров , .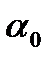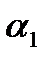