С равномерным распределением на интервале (0., 1.)

Эта же функция может быть использована для построения плотности вероятности равномерного распределения на произвольном интервале : .

Пример:

y=rand(10000,1); % Выборкаобъема n=10000;

x=-0.5:0.01:1.5; a=0; b=1;

w=unifpdf(x, a, b);

plot(x,w)

2.2 . Формирование вещественного массива выборочных значений случайной величины, имеющей стандартное нормальное (гауссовское) распределение

Синтаксис:

y=randn(n,1)

Описание:

Функция MATLABy=randn(n,1)формирует матрицу размера , элементами которой являются выборочные значения случайной величины, имеющей нормальное (гауссовское) распределение с математическим ожиданием0 и дисперсией 1.

Аналитическое выражение плотности вероятности стандартной гауссовской случайной величины имеет вид:

, .

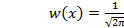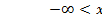На рис. 3 изображен график плотности вероятности гауссовской случайной величины с математическим ожиданием 0 и дисперсией 1, построенной с помощью функции MATLABw=normpdf(x).

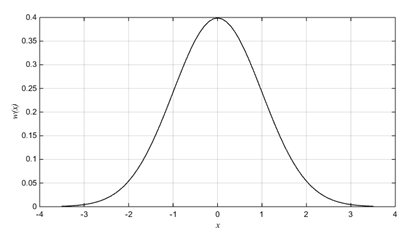
Рис.3. Плотность вероятности стандартной гауссовской случайной величины

Пример:

y=randn(10000,1); % Выборкаобъема n=10000;

x=-4:0.01:4;

w=normpdf(x);

plot(x,w)

Эта же функция может быть использована для построения гауссовской плотности вероятности с произвольными значениями математического ожидания и дисперсии.

2.3 . Формирование вещественного массива выборочных значений случайной величины, имеющей распределение хи-квадрат

Синтаксис:

y=сhi2rnd(V,n,m)

Описание:

Функция MATLABy=сhi2rnd(V,n,m) формирует вещественную матрицу размера , элементами которой являются выборочные значения случайной величины, имеющей хи-квадрат распределение с V степенями свободы.

Здесь приняты следующие обозначения:

y - формируемая выборка;

V - число степеней свободы хи-квадрат распределения, целое положительное число.

Аналитическое выражение плотности вероятности случайной величины c распределением хи-квадрат имеет вид:

, ,

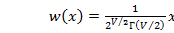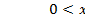где - гамма-функция.

На рис.4 изображен график плотности вероятности случайной величины с распределением хи-квадрат, построенный с помощью функции MATLABw=chi2pdf(x,V).

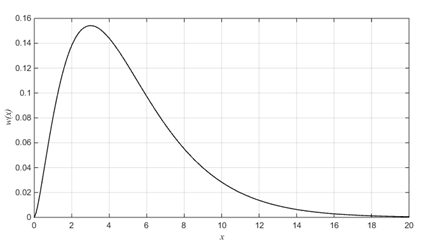
Рис.4. Плотность вероятности хи-квадрат распределения, V=5

При это распределение совпадает с экспоненциальным.

Пример:

y= сhi2rnd(V,10000,1); % Выборкаобъема n=10000;

x=0:0.01:20;

w=chi2pdf(x,5).

plot(x,w)

2.4 . Формирование вещественного массива выборочных значений случайной величины, имеющей распределение Райса (обобщенное распределение Релея)

Синтаксис:

pd = makedist(‘rician’, ‘s’, 4, ‘ ’, 2);

y=random(pd, n, 1);

Описание:

Функция MATLABpd = makedist(‘rician’, ‘s’, 4, ‘ ’, 2) создает скрипт-файлраспределения Райса с параметрами нецентральности и масштаба (обобщенное распределение Релея).

Функция MATLABy=random(pd, n, 1) генерирует массив yразмера , элементами которого являются выборочные значения случайной величины, имеющей распределение pd.

Аналитическое выражение для плотности вероятности этой случайной величины имеет вид:

, ,

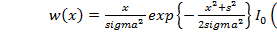где – модифицированная функция Бесселя.

Пример графика этой плотности для 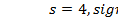приведен на рис.5; график рассчитан с помощью функции MATLAB 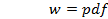, где – массив значений аргумента плотности вероятности, для которого вычисляются значения плотности .

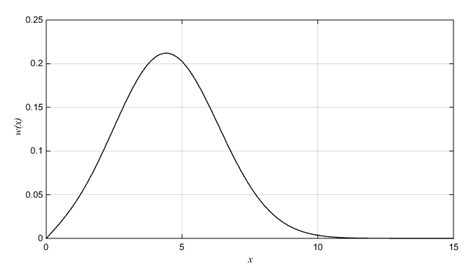
Рис.5. Плотность вероятности случайной величины,