Глава 4. Аналитическая геометрия в пространстве.

Метод координат в пространстве.

4.1.1. На оси Оу найти точку, равноудалённую от двух точек А (2;3;1) и В (-1;5;-2).

Решение: Точка М, лежащая на оси Оу, имеет координаты М (0;у;0). По условию задачи

. Найдем расстояния и :

= ;

= .

Получим уравнение:

Отсюда находим, что 4y=16, т.е. y=4. Искомая точка есть М(0;4;0).

4.1.2. Найти координаты точки на плоскости Оху, равноудаленной от трех точек: А(4;0;2), В(-1;2;4), С(1;1;-3).

4.1.3. Показать, что треугольник с вершинами в точках А(-3;2;4), В(0;-2;-1), C(1;5;9) равнобедренный.

4.1.4. Отрезок АВ разделен на 3 равные части. Найти координаты точек деления, если известны точки А(-2;4;1) и В(2;-4;-3).

4.1.5. Дана точка А(3;-4;2). Найти координаты точки, симметричной данной относительно координатных плоскостей, осей координат, начала координат.

4.1.6. Дан треугольник с вершинами в точках А(5;2;4), В(-3;6;0), С(3;2;-4). Найти длину его медианы, проведенной из вершины А.

4.1.7. Показать, что треугольник с вершинами в точках А(8;0;6), В(2;-4;2), С(6;-6;-2) прямоугольный.

4.1.8. Найти координаты точки на оси Оz, удаленной от точки М(-2;-1;4) на 3 единицы.

4.1.9. Даны вершины треугольника А(1;-1;3), В(-5;2;-6), С(2;1;-2) Найти длину биссектрисы его внутреннего угла при вершине А.

4.1.10. Лежат ли на одной прямой точки А(2;-3;1), В(0;-11;3) и С(4;5;-1)?

4.1.11. В каких октантах могут быть расположены точки, координаты которых удовлетворяют одному из следующих условий:

1) х-у=0;

2)х+z=0;

3)ху>0;

4)хуz<0?

4.1.12. Найти центр и радиус сферы, которая проходит через точку А(4;-1;-1) и касается всех трех координатных плоскостей.

4.1.13. Найти расстояние от точки А(3;-4;5) до начала координат и до осей координат.

4.1.14. Даны две вершины параллелограмма АВСD: А(1;1;-1), В(-2;3;0) и точка пересечения его диагоналей М(4;0;3). Найти координаты вершин С и D.

4.1.15. Найти уравнение сферы радиуса R с центром в точке О₁(a,b,c).

Решение: В прямоугольной системе координат Оxyz точка О₁- центр сферы – имеет координаты a, b и c. Пусть М(х;у;z) – произвольная точка сферы. Тогда О₁М= R, или

Окончательно получаем уравнение сферы

.

4.1.16. Найти координаты центра и радиуса сферической поверхности, заданной уравнением .

4.1.17. Как расположены точки А(0;5;7), В(-3;4;0), С(0;0;6) относительно сферы?

Плоскость в пространстве.

4.2.1. Составить уравнение плоскости, проходящей через:

1) точку М(-2;3;1) параллельно плоскости Оху;

2) точку М и ось Оу.

Построить эти плоскости.

4.2.2. Составить уравнение плоскости, проходящей через:

1) точку А(5;-4;6) перпендикулярно оси Ох;

2) точку А и отсекающей равные отрезки на положительных координатных полуосях.

Построить эти плоскости.

4.2.3. Определить направляющие косинусы радиус-вектора, перпендикулярного к плоскости 3х-4у+5х-10=0.

4.2.4. Написать уравнение плоскости:

1) параллельной оси Оz и проходящей через точки М₁(3;-1;2) и М₂(-1;2;5);

2) проходящей через точку М₁ перпендикулярно вектору .

4.2.5. Составить уравнение плоскости, проходящей через точку М₀(2;3;-4) и параллельной векторам 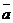=(-3;2;-1) и 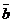=(0;3;1).

4.2.6. Написать уравнение плоскости, проходящей через точкиМ₁(2;0;-1), М₂(-3;1;3) параллельно вектору =(1;2;-1).

4.2.7. Написать уравнение плоскости, проходящей через точку М(1;-1;0), параллельно векторам 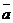=(0;2;3) и 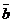= (-1;4;2).

4.2.8. Написать уравнение плоскости, проходящей через три заданны точки М₁(1;0;-1), M₂(2;2;3), М₃(0;-3;1).

4.2.9. Составить уравнение плоскости, проходящей через точки М₁(-2;0;0), М₂(0;4;0), М₃(0;0;0).

4.2.10. Составить уравнение пересечения плоскостей 2х-y+2z-6=0 и 3х+2y-z+3=0.

4.2.11. Найти уравнение плоскости, проходящей через точку М(1;1;1) перпендикулярно к линии пересечения двух плоскостей x-y+2z-3=0 и 2x-z+4=0

4.2.12. Найти уравнение плоскости, проходящей через линию пересечения двух плоскостей x-2y+3z-4=0 и x+y-5z+9=0 и параллельны оси Ох.

Разное.

4.2.13. Найти объем пирамиды, ограниченной плоскостью x+3y-5z-15=0 и координатными плоскостями.

4.2.14. Найти длину перпендикуляра, опущенного из начала координат на плоскость 20x-5y+4z-210=0 и угол, образованный этим перпендикуляром с осью Оz.

4.2.15. Найти плоскость, зная, что точка М(2;-4;4) служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.

4.2.16. Найти геометрическое место точек, равноудаленных от точек М₁(2;1;-2) и

М₂(-2;3;4).

4.2.17. Найти уравнение плоскости, отсекающей на отрицательной полуоси Оy отрезок, равный 4, и перпендикулярной вектору

4.2.18. Составить уравнение плоскости, проходящей через точки М₁(4;2;3) и М₂(2;0;1) и перпендикулярной к плоскости x+2y+3z+4=0.

4.2.19. Составить уравнение плоскости, проходящей через точку М(1;0;3) и перпендикулярной к плоскостям x+y+z-8=0 и 2x-y +4z+5=0.

4.2.20. Составить уравнение плоскости, проходящей через точки М₁(1;2;3) и М₂(-2;-3;4) и пересекающей оси Оx и Оz в точках с равными и положительными координатами.

4.2.21. Найти расстояние от начала координат до плоскости, которая пересекает оси Ох, Оу, Оz в точках с координатами а=-6, b=3, c=3.

4.2.22. Найти уравнение плоскости, проходящей через основания перпендикуляров, опущенных из точки М (2;2;2) на координатные плоскости.

4.2.23. Составить уравнение плоскости, проходящей через точку М(2;-2;5) и отсекающей на осях Оx и Oy втрое большие отрезки, чем на оси Оz.

4.2.24. Составить уравнение плоскости, проходящей через точку М₁ перпендикулярно вектору , зная точку М₂(2;-8;-1).

4.2.25. Найти точку пересечения следующих плоскостей:

1) x-3y+2z-11=0, x-2y+z-7=0, 2x+y-z+2=0;

2) 3x+y+z-5=0, x-4y-2z+3=0, 3x-12y-6z+7=0.

4.2.26. Составить уравнение плоскости проходящей через точку М(-4;-3;-2), параллельно плоскости х+2у-3z-6=0.

4.2.27. Составить уравнение плоскости, проходящей через точку М(0;-2;-1) параллельно плоскости, проходящей через три точки М₁(0;-2;-1), М₂(1;-3;4), М₃(1;1;-1).

4.2.28. Найти величину острого угла между плоскостями:

1) 11х-8у-7z-1=0 и 4x-10y+z-2=0;

2) 2x+3y-4z+4=0 и 5x-2y+z-3=0.

4.2.29. Найти величину острого угла между плоскостями:

1) х+у-2х+5=0 и 2х+3у+z-2=0;

2) 2х-2у+z=0 и z=0.

4.2.30. Написать уравнение плоскости, параллельной плоскости х-2у+2z+5=0 и удаленной от точки М(3;4;-2) на расстояние d=5.

4.2.31. Найти расстояние между параллельными плоскостями:

1) х+у-z-2=0 и 2x+2y-2z+5=0;

2) 2х-3у+6z-14=0 и 2x-3y+6z+42=0.

4.2.32. Найти расстояние от точки М₀(5;4;-1) до плоскости, проходящей через точки М₁(0;4;0), М₂(0;4;-3), М₃(3;0;3).

4.2.33. Составить уравнение плоскости, проходящей через точки М₁(-1;3;0) и М₂(2;4;-1), перпендикулярно плоскости х-2у+3z-10=0.

4.2.34. Составить уравнение плоскости, проходящей через начало координат и точку М(2;1;-1) перпендикулярно плоскости 2х-3z=0.

4.2.35. Установить какие из следующих пар плоскостей являются параллельными, какие - перпендикулярными:

1) 3x+4y-z+8=0 и 6x+8y-2z-12=0;

2) 3x-6y+3z-12=0 и –x+2y-z+4=0;

3) x+2y-5z+1=0 и 2x+4y+2z-7=0.

4.2.36. Составит уравнение плоскости, проходящей через точку М(4;0;2) и перпендикулярной плоскостям x+y+z=0 и y-z=0.

4.2.37. Найти координаты точки на оси Оу, равноудалённой от двух плоскостей x+2y-2z+6=0 и 2x+y+2z-9=0.

4.2.38. Дана пирамида с вершинами А(2;2;-3), В(3;1;1), С(-1;0;-5), D(4;-2;-3). Найти длину высоты, опущенной из вершины D на грань АВС.

4.2.39. Составить уравнение плоскости, расположенной на расстоянии четырёх единиц от плоскости 3x-6y-2z+8=0 и параллельно ей.

4.2.40. Доказать, что параллелепипед, грани которого лежат в плоскостях 8x-4y+5z-7=0, 3x+y-4z+13=0, 11x+47y+20z+2=0, является прямоугольным.

4.2.41. Найти объем куба, две грани которого лежат на плоскостях 13x+5y+ z-5=0 и 13x+5y+ z+23=0.

4.2.42. Даны уравнения трех граней параллелепипеда х+4=0, у+2z-5=0, x-3y+4z-12=0 и одна из его вершин (4;-3;2). Найти уравнения трех других граней параллелепипеда.

4.2.43. Составить уравнение плоскости, проходящей через линию пересечения плоскостей 2x-y-12z-3=0 и 3x+y-7z-2=0 перпендикулярно плоскости 4x-2y+25=0.

4.2.44. Определить уравнение плоскости, проходящей через ось Оу и составляющей с плоскостью x+ y-z-3=0 угол 60⁰.

Прямая в пространстве.

4.3.1.Найти направляющий вектор прямой

4.3.2 Привести к каноническому виду прямую

4.3.3. Найти параметрические уравнения прямой:

1) проходящей через точку (1;0;1) и параллельной вектору

2) проходящей через точки (2;2;2) и (6;2;1).

4.3.4. Составить канонические уравнения прямой, проходящей через точку Мо (4;3;-2) параллельно

1) вектору

2) прямой

4.3.5. Найти уравнение прямой, проходящей через точку (3;-2;5);

1) параллельно оси Оz;

2) параллельно прямой

4.3.6. Проверить, лежит ли точка М(1;-3;2) на прямой

4.3.7. Проверить, лежат ли на одной прямой три данные точки (-3;5;4), (2;4;6), (2;14;6).

4.3.8. Привести к каноническому виду уравнение прямой

4.3.10. Найти точки пересечения прямой с координатными плоскостями.

4.3.11. Найти точки пересечения прямой

с координатными плоскостями.

4.3.12. Найти уравнение прямой, проходящей через точку М(-4;2;2) и пересекающей ось Оz под прямым углом.

4.3.13. Составить уравнение прямой, проходящей через точку М(1;-1;2) и перпендикулярной векторам и 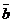=(-2;5;0).

4.3.14.Составить канонические уравнения прямой, проходящей через точку V(1;3;-2) и образующей с осями Ох, Оу, Оz углы 120⁰, 60⁰, 45⁰ соответственно.

4.3.15.При каких значениях D прямая пересекает ось Ох?

4.3.16. Даны вершины треугольника А(-3;2;8), В(-7;0;3), C(3;4;5). Cоставить параметрические уравнения его медианы, проведенной из вершины А.

4.3.17. Даны две вершины параллелограмма ABCD: F(8;1;5) и D(-3;0;4) и точка пересечения диагоналей J(2;4;-2). Найти уравнение стороны ВС.

4.3.18. Найти величину острого угла между прямыми

и

Решение: Направляющий вектор первой прямой есть ₁=(-3;1;-2). Находим направляющий вектор 2 второй прямой:

₂= т.е. ₂=(-1;5;3).

cosj=

поэтому j=arccos (~ ).

4.3.19. Найти величину острого угла между прямыми:

1) и

2) и .

4.3.20. Установить взаимное расположение прямых:

1) и

2) и .

Решение: 1) Выпишем направляющие векторы первой и второй прямых: ₁=(4;3;-2),

₂=(-8;-6;4). Как видно, координаты этих векторов пропорциональны:

Следовательно, данные прямые параллельны или совпадают. Возьмем на первой прямой какую-нибудь точку, например точку (2;0;-1). Подставим ее координаты в уравнение второй прямой:

Получаем t= - из первого уравнения, t= - из второго, t=-1 – из третьего. Это означает, что точка (2;0;-1) не принадлежит второй прямой; прямые не совпадают. Значит они параллельны.

2) Координаты направляющих векторов ₁=(2;-3;1) и ₂=(3;2;4) данных прямых не пропорциональны. Следовательно, прямые либо пересекающиеся, либо скрещивающиеся. Проверим выполнение условия принадлежности двух прямых одной плоскости, предварительно выписав координаты точек М₁ и М₂, через которые проходят данные прямые:

М₁(0;1;-2), М₂(-4;-3;1). Имеем:

= = -4 +4 +3 =

=-4*(-14)+4*5+3*13=115≠0.

следовательно, данные прямые – скрещивающиеся.

4.3.21. Выяснить взаимное расположение прямых:

1) и

2) и

4.3.22. Найти уравнение прямой, проходящей через точку М₁(-2;3;4) и перпендикулярной прямым

и

Решение: Уравнение искомой прямой имеет вид

.

Найдем m,n,p – координаты направляющего вектора этой прямой. Используя условие перпендикулярности прямых, можно записать:

По правилу решения системы двух линейных однородных уравнений с тремя неизвестными находим:

Уравнение искомой прямой есть

или

Замечания: 1) Систему уравнений

можно переписать в виде

Отсюда , т.е. m:n:p = -5:1:3, поэтому m=-5t, n=t, p=3t, где t- число.

2) В качестве вектора можно использовать вектор _{1 2}, так как искомая прямая перпендикулярна данным прямым. Тогда

= + + т.е. m=-5, n=1, p=3.

4.3.23. Составить канонические уравнения прямой, лежащей в плоскости Оxy, проходящей через начало координат и перпендикулярной к прямой

4.3.24. Составить уравнение прямой, проходящей через точку М₁(1;-2;3) и перпендикулярной к прямым

4.3.25. Найти расстояние от точки М(-5;4;3) до прямой

4.3.26. Найти расстояние между параллельными прямыми и Указание. Воспользоваться формулой S .

4.3.27. Проверить, лежат ли прямые в одной плоскости

и

4.3.28. В уравнении прямой найти параметр n, при котором эта прямая пересекается с прямой найти координаты точки их пересечения.

Глава 5. Введение в анализ.

Функции и их графики.

5.1.1. Найти область определения функций:

1) ;

2) ;

3) .

Решение: 1) Дробь определена, если ее знаменатель не равен нулю. Поэтому область определения данной функции находится из условия х²-1 0, т.е. х 1. Таким образом, D(f)=(- ;-1) (-1;1) (1;+ ).

2) Функция определена, если подкоренное выражение неотрицательно, т.е. 5-3х 0. Отсюда х , и, значит, D(f)=(- ; .

3) Выражение, стоящее под знаком логарифма, должно быть положительным, поэтому функция ln(x+2) определена в том и только в том случае, когда х+2 0, т.е. х -2. Значит, D(f)=(-2;+ ).

5.1.2. Найти область определения функций:

1) f(x)= ;

2) f(x)=

Решение:1) Функция , a>0 определена при всех действительных значениях х, поэтому функция определена в точности при тех значениях х, при которых имеет смысл выражение т.е. при х≠0. Далее область определения второго слагаемого находим из двойного неравенства -1≤ ≤1. Отсюда -3≤ х+2 ≤3, т.е. -5≤ х ≤1.

Область определения функции f(x) ест пересечение областей определения обоих слагаемых, откуда D(f)=[-5;0)U(0;1]

2) Функция 7cos2x определена при всех действительных значениях х, а функция - лишь при тех значениях х, при которых 2х-х²≠0, т.е. при х≠0, х≠2. Таким образом, D(f)=(-∞;0)U(0;2)U(2;+∞).

Найти область определения функций:

5.1.3. f(x)=. 5.1.4. f(x)=sin

5.1.5. f(x)= (-x). 5.1.6. f(x)=

5.1.7. f(x)= +tgx. 5.1.8. f(x)= .

5.1.9. f(x)= . 5.1.10. f(x)= 5.1.11. f(x)= 5.1.12. f(x)= arccos(x-2)-ln(x-2)

5.1.13. Найти множества значений функций:

1) f(x)= ;

2) f(x)= ;

3) f(x)= 3-5сosx.

Решение: 1) Так как = ,а (х+2)²≥0 для всех значений х, то f(x)=≥-3 для всех х. Поскольку к тому же функция (х+2)² принимает все значения от 0 до ∞, то Е(f)=[-3;+∞).

2)Е(х²)=[0;+∞), поэтому множество значений функции совпадает с множеством значений функции 2^хпри х≥0. Отсюда Е(f)=[1;+∞).

3)E(cosx)=[-1;1], откуда Е(-5cosx) = [-5;5] Так как f(x) = -5cosx+3, то Е(f)=[-2;8].

Найти множество значений функций.

5.1.14 f(x) = . 5.1.15 f(x) = .

5.1.16 f(x) = 2sinx-7. 5.1.17 f(x) = .

5.1.18 f(x) = . 5.1.19 f(x) = .

5.1.20. Для функций f(x) = найти:

1) f(0); 2) f(-2); 3) f( ); 4) f(-х);

5) f( ); 6) f(a+1); 7) f(a)+1; 8) f(2x).

Решение: 1) -3) Подставляя значение х=0 в аналитическое выражение для данной функции, получим: f(0)= . Аналогично находим

4) -6). Для того, чтобы найти f(-x), надо формально заменить х в формуле для f(x) на –х. Тогда Точно так же найдем

,

7)

8)

5.1.21. Для функции Найти:

1) f (1); 2) f (-3); 3) f ( ; 4) f (-x); 5) f (3x);

6) f ( ; 7) 8) f (b-2).

5.1.22 Для функции φ(t)= найти:

1) φ(-1); 2) φ(-5); 3) φ( ); 4) 1) φ(z+3); 1) φ(2t-1).

5.1.23. Какие из следующих функций четные, какие нечётные, а какие – общего вида:

1) f(x) = ;

2) f(x) =

3) f(x) =

4) f(x) = ln

Решение: 1) D(f)=(-∞;+∞) и стало быть, область определения функции симметрична относительно начала координат. кроме того,f(-x) = = - f(x), т.е. данная функция нечетная.

2) D(f)=(-∞;+∞) и f(-x) = Следовательно, функция четная.

3) D(f)=(-∞;+∞) и f(-x) = ≠± f(x), т.е. данная функция общего вида.

4) D(f)=(-1;1), т.е. область определения симметрична относительно нуля. к тому же f(x) = ln = ln ln =-f(x), т.е. функция нечетная.

5.1.24 Какие из следующих функция четные, какие нечетные, а какие - -общего вида:

1) f(x) = 2) f(x) = 3) f(x) = ; 4) f(x) = arcsinx;

5) f(x) = sinx+cosx; 6) f(x) = ; 7) f(x) = ; 8) f(x) = x∙ ;

5.1.25. Определить, является ли данная функция периодической, и найти ее наименьший положительный период, если он существует:

1) f(x) = sin4x; 2) f(x) = ; 3) f(x) = 4) f(x) = sin2x+cos3x;

5) f(x) = .

Решение: 1) Наименьшим положительным периодом функции sinx является число 2П. Покажем, что наименьший положительный период sin4x – число

Действительно, , т.е - период данной функции. С другой стороны, если - какой – либо другой период этой функции, то для всех x, т.е. . Отсюда следует, что 4Т₁-период функции sin t, где , и, значит, , т.е.

Таким образом, - наименьший положительный период функции sin 4x.

2). Поскольку , то период данной функции совпадает с периодом функции cos10x. Рассуждая как и в пункте 1), легко показать, что наименьший положительный период функции cos10x равен Таким образом, наименьший положительный период функции равен

3). Наименьший положительный период tgx равен ,поэтому наименьший положительный период функции будет равен (см. рассуждения в пункте 1))

4). Наименьшие положительные периоды функций и соответственно равны (см. пункты 10 и 2)) , т.е. и . Нетрудно показать (см.также задачу 6.1.124), что наименьший положительный период суммы этих функций будет равен наименьшему общему кратному их периодов, т.е числу .

5). При функция определена и возрастает, поэтому не может быть периодической. Значит, на интервале функция не является периодической.

5.1.26. какие из следующих функций периодические, а какие – нет? Там, где это возможно, найти наименьший положительный период функции:

1).

2). ;

3).

4).

5).

Разное.

Найти области определения функций:

5.1.27. 5.1.28.

5.1.29. 5.1.30.

5.1.31. 5.1.32.

5.1.33. 5.1.34.

5.1.35. 5.1.36.

Найти множество значений функции:

5.1.38. 5.1.39.

5.1.40. 5.1.41.

5.1.42. 5.1.43.

5.1.44. 5.1.45.

5.1.46.

Найти y(0), y(2), для функции y(х):

5.1.47. 5.1.48.

5.1.49. Решить уравнение , где

5.1.50. выяснить, какие из следующих функций являются четными, какие – нечетными, а какие – функциями общего вида:

1).

2).

3).

4).

5).

6).

7).

8).

5.1.51. Дана функция Доопределить ее на интервале так, чтобы новая функция g(x), определенная на интервале , была:

1). Четной

2). Нечетной

3). Функцией общего вида.

5.1.52. выяснить, какие из следующих функций периодические, и определить их наименьший положительный период:

1).

2).

3).

4).

Построить графики функций:

5.1.53. 5.1.54.

5.1.55. 5.1.56.

5.1.57. 5.1.58.

5.1.59. 5.1.60.

5.1.61. 5.1.62.

5.1.63. 5.1.64.

5.1.65. (читается сигнум х), где sign x =

5.1.66. найти сложные функции и если:

1)

2) (см. задачу 5.1.65.),

3)

4)

Какие из следующих функций имеют обратные? Для таких функций найти обратные функции.

5.1.67. 5.1.68.

5.1.69.

Выяснить, какие из следующих функций монотонные, какие – строго монотонные, а какие – ограниченные:

5.1.70. 5.1.71.

5.1.72. 5.1.73.

5.1.74. 5.1.75.

5.2. Предел последовательности.

5.2.1. найти пределы последовательностей:

1).

2). ;

3).

Решение: 1). Преобразуем выражение, стоящее под знаком предела, поделив числитель и знаменатель на старшую степень n, т.е. отсюда, используя теорему о действиях над пределами, получим:

В последних равенствах мы воспользовались тем, что предел константы – константа, а также тем, что последовательности и - бесконечно малые.

Окончательно,

2). Домножим и разделим выражение под знаком предела на сопряженное к нему, после чего воспользуемся формулой разности квадратов:

Поэтому

Поскольку последовательность - бесконечно большая, то последовательность - бесконечно малая. Отсюда

, а значит, и

3). Поделим числитель и знаменатель дроби на старшую степень n (выбираем из двух вариантов и ), т.е. на . Тогда

Оба слагаемых в знаменателе последней дроби, т.е. и , бесконечно малые последовательности, следовательно, вся эта дробь – бесконечно большая последовательность. Отсюда

Найти пределы:

5.2.2. 5.2.3.

5.2.4. 5.2.5.

5.2.6. . 5.2.7.

5.2.8. 5.2.9.

5.2.10. 5.2.11.

Найти пределы.

5.2.12. 5.2.13.

5.2.14. 5.2.15.

5.2.16. 5.2.17.

5.2.18. 5.2.19.

5.2.20. если

5.2.21.

Предел функции.

5.3.1. Используя свойства пределов функций, найти следующие пределы:

1).

2).

3).

Наши рекомендации

II. Аналитическая геометрия в пространстве

Аналитическая геометрия в пространстве.

Аналитическая геометрия в пространстве

Iv. аналитическая геометрия в пространстве

Аналитическая геометрия в пространстве

Аналитическая геометрия в пространстве.

Аналитическая геометрия в пространстве

Аналитическая геометрия в пространстве.

Аналитическая геометрия в пространстве

I. Аналитическая геометрия на плоскости и в пространстве.

← Предыдущая страница | Следующая страница →