Системы управления движением
Системы управления движением
Ошибки программных движений. Системы с обратными связями
Важной задачей, актуальной как для машин с программирующими механизмами, так и для агрегатов с программным управлением, является обеспечение точности выполнения программных движений. В реальной машине законы движения рабочих органов не совпадают с программными. Отклонения действительных законов от программных будут в дальнейшем называться динамическими ошибками. Причинами возникновения динамических ошибок являются различные возмущающие факторы: в первую очередь, они связаны с несоответствием действительных свойств функциональных частей машины идеализированным моделям, принятым при их расчёте и проектировании, а также с неточными представлениями о характере рабочих процессов, выполняемых машиной, и, в частности, о значениях активных сил, возникающих при их выполнении.
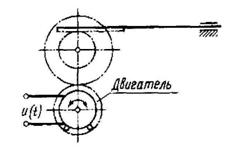
Рисунок 1.13 – Программное управление движением
Одним из способов уменьшения динамических ошибок является использование обратных связей. На рисунке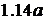 
показана принципиальная схема системы программного управления двигателем однодвигательной машины с обратной связью. Здесь производится измерение закона движения 
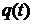выходного звена двигателя Д и сравнение его с требуемым программным движением 
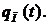Сигналы рассогласования 
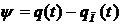поступают в регулятор машины P, в котором формируется сигнал 
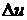, складывающийся с сигналом программного управления 
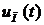и тем самым корректирующий закон движения (т. е. уменьшающий динамическую ошибку).
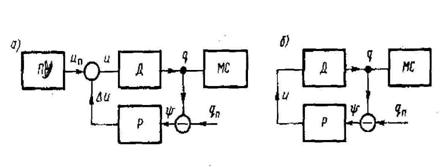
Рисунок 1.14 – Схемы программного управления с обратной связью
На рисунке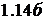 
представлена схема следящей системы, в которой программное управление целиком формируется по сигналу динамической ошибки.
Принцип обратной связи используется и в машинах программирующими механизмами для стабилизации угловой скорости ротора двигателя. При отклонении угловой скорости от её программного значения, вызванного, например, изменением нагрузки на двигатель, система обратной связи формирует сигнал, изменяющий значение входного параметра двигателя.
Силовой анализ механизмов
Постановка задачи
При силовом анализе движение механизма считается известным, т.е. предполагается, что законы изменения всех кинематических параметров (координат, скоростей, ускорений точек механизма, угловых скоростей и ускорений его звеньев) являются известными функциями времени. Предполагается так же, что силы сопротивления, возникающие при выполнение рабочего процесса, являются известными функциями от кинематических параметров движения. Заданными считаются и все другие активные силы, действующие на звенья механизма (силы тяжести, силы, создаваемые конструктивными упругими элементами, например, пружинами и т.д.), кроме обобщённых движущих сил. Считаются известными кинетические параметры звеньев (массы и моменты инерции), что предполагает предварительную разработку конструкции механизма, его узлов и деталей.
В процессе силового анализа определяют:
а) обобщённые движущие силы (силы или моменты сил), которые должны быть приложены к входным звеньям механизма для преодоления сил сопротивления и осуществления заданного движения;
б) реакции в кинематических парах.
Определив обобщённые движущие силы и вычислив мощности этих сил на заданном движении, конструктор может выбрать двигатели и перейти к следующему этапу динамического исследования - анализу движения машины с учётом характеристики двигателей. Определив реакции в кинематических парах, можно приступить к расчёту их конструктивных элементов на прочность, жёсткость, надёжность и долговечность.
Найдём количество неизвестных величин, подлежащих определению при силовом анализе. В любом механизме число обобщённых движущих сил должно равняться числу входных пар или числу входных звеньев (если одним из звеньев каждой входной пары является стойка), следовательно и числу степеней подвижности w, которое в случае механизма с жёсткими звеньями совпадает с числом его степеней свободы. Эти силы, приложенные к входным звеньям механизма, будут обозначаться через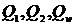 
, а для механизма с одной степенью подвижности через 
.
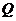Реакции в кинематических парах относятся к пассивным силам. Если не вводить каких-либо дополнительных предположений о свойствах кинематических пар, то в любой кинематической паре неизвестными будут шесть скалярных компонент реакции: три проекции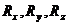 
главного вектора 
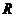сил реакции на оси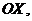 
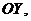
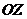и три проекции на те же оси 
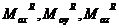главного момента 
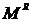этих сил относительно точки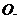 
Пусть механизм имеет 
степеней подвижности и 
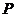кинематических пар.
Тогда общее число неизвестных, подлежащих определению при силовом анализе, равно
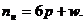
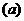
Если механизм имеет Nn подвижных звеньев, то общее число уравнений, используемых для силового анализа, равно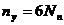 
. Для каждого механизма, не обладающего избыточными связями, справедлива структурная формула
, 
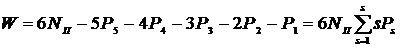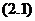
где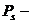 
число кинематических пар класса s.
Отсюда число уравнений
. 
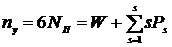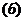
Сравнивая 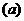и 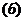и учитывая 
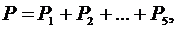получаем
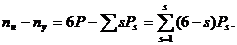
Таким образом, число неизвестных превышает число уравнений и задача силового анализа в общем случае оказывается неразрешимой. Чтобы сделать её разрешимой, необходимо ввести дополнительные предположения, уточняющие динамическую модель системы и снижающие число неизвестных.
Идеальные связи
Одним из предположений, позволяющих уменьшить число неизвестных реакций, является предположение об идеальности связей. Связь называется идеальной, если сумма работ всех реакций на любом возможном перемещении равна нулю. Отсюда следует, что в направлении возможных перемещений в кинематической паре должны отсутствовать соответствующие реакции.
Так, вращательная пара 5 класса допускает только одно возможное перемещение: поворот вокруг оси oz на произвольный угол 
. При этом реакции совершают возможную работу
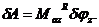
Для идеальной связи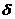 
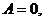следовательно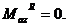 
Кинематическая пара S-го класса обладает 6-S степенями подвижности в относительном движении, то есть 6-S перемещений могут задаваться произвольно. Тогда 6-S компонент реакции должны быть либо равны нулю, либо выражаться через остальные S компонент. Например, в винтовой паре при повороте винта на произвольный угол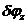 
гайка перемещается вдоль оси на расстояние
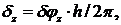
где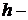 
шаг винта. При этом возможная работа
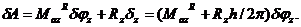
Если связь считать идеальной, то:
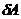
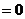и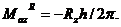 
Таким образом, остается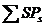 
неизвестных реакций, и задача силового анализа становится разрешимой.
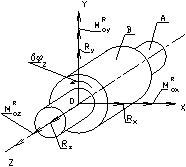
Рисунок 2.1 – Вращательная пара 5 класса
На практике широко применяются плоские механизмы, у которых все нагрузки, оси звеньев находятся в одной плоскости; в той же плоскости осуществляется и движение.
Для плоских механизмов при наличии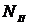 
подвижных звеньев можно составить 
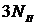уравнений кинетостатики. При идеальных связях в низших кинематических парах плоских механизмов возникают две реакции. В поступательной паре возникает реактивный момент 
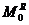и сила реакции 
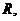приложенная к геометрическому центру пары 
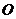и направленная по нормали к контактирующим поверхностям 
. Во вращательной паре направление реакции неизвестно, поэтому её раскладывают на две составляющие по осям 
.
В высшей кинематической паре возникает одна реакция, приложенная в точке контакта рабочих профилей 
и направленная по нормали к профилям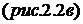 
.
Рисунок 2.2 – Реакции в плоских кинематических парах
Предположение об идеальности связей эквивалентно предположению об отсутствии сил трения в кинематической паре.
При конструировании механизма обычно стремятся к уменьшению сил трения. Поэтому часто эти силы малы и их влиянием в первом приближении можно пренебречь. Однако в некоторых механизмах трение в кинематических парах является существенным. В этих случаях используются другие предположения, также приводящие к уменьшению числа неизвестных.
Уравнения кинетостатики
Для определения неизвестных сил используются уравнения равновесия звеньев, составленные по принципу Даламбера.
Силы, приложенные к звену, разделим на активные силы и реакции кинематических пар 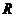. Введём в рассмотрение силы инерции
.
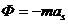Тогда уравнения кинетостатики в векторном виде можно записать так
, 
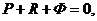
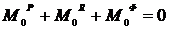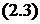
где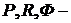 
главные векторы активных, реактивных сил и сил инерции; 
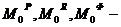их главные моменты относительно некоторой точки (полюса).
Выразим главный вектор и главный момент сил инерции звена через его кинетические и кинематические параметры, используя известные соотношения из аналитической механики.
Главный вектор
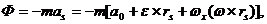
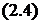
где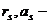 
радиус-вектор и ускорение центра масс звена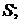 
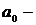ускорение полюса 
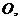связанного с движущим звеном; 
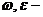абсолютная угловая скорость и ускорение звена;
знак «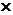 
» означает векторное произведение.
Напомним, что векторное произведение двух векторов равно
, 
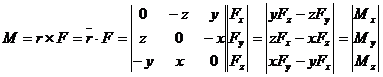где 
кососимметричная матрица, составленная из проекции вектора 
на оси координат.
Выражение для главного момента сил инерции относительно подвижного полюса 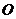имеет вид [3]
, 
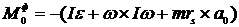где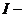 
тензор инерции звена в точке .
Если выбрать систему координат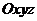 
, связанную с движущимся звеном, то тензор 
может быть описан матрицей
. 
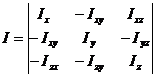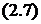
Здесь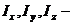 
осевые, а 
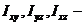центробежные моменты инерции звена относительно осей .
; 
;
; 
; 
; 
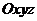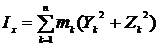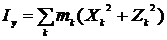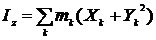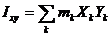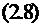
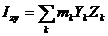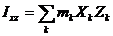
Произведения 
и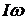 
определяются по правилам умножения матрицы на вектор
,
.
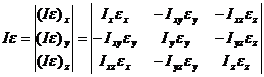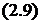
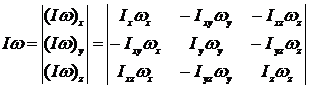Найдём проекции на оси векторов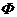 
и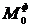 
для некоторых частных случаев движения звена.
Поступательное движение. В этом случае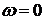 
, 
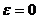. Ускорения всех точек одинаковы, поэтому 
.
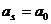Отсюда
; 
. 
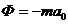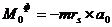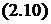
Проектируя 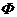на оси, получаем:
, 
, 
.
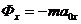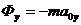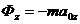Проекции момента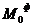 
на оси найдём с учётом :
;
; 
.
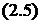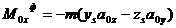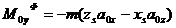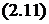
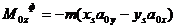Вращение вокруг неподвижной оси .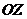
Тогда:
, 
; 
; 
; 
.
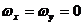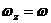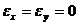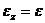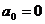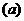
Выражение 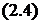теперь примет вид
,
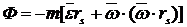где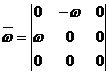 
, 
.
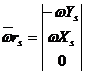Матрица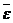 
совпадает с матрицей 
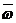, заменой в ней 
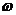на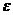 
. После перемножения матриц получаем:
, 
, 
. 
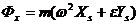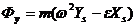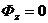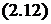
Из выражения 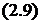с учётом имеем:
, 
, 
,
, 
, 
.
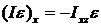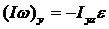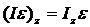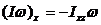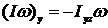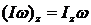Далее находим проекции на оси векторного произведения
.
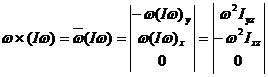Подставив найденные выражения в 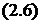, определяем проекции момента сил инерции на оси координат:
; 
; 
. 
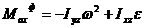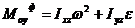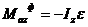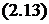
Плоскопараллельное движение. Ось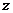 
направим перпендикулярно плоскости движения, а в качестве полюса выберем центр масс 
.
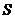Тогда:
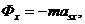
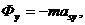
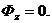
Проекции момента определяются выражением 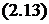, в котором тензор инерции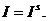 
Системы управления движением