Площадь криволинейной фигуры
Площадь криволинейной трапеции, ограниченной сверху графиком непрерывной функции 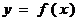 , слева и справа соответственно прямыми
, слева и справа соответственно прямыми 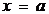 и
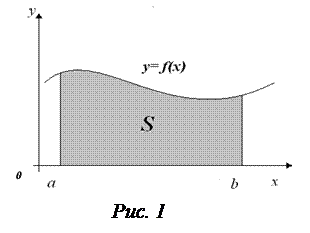
и 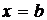 , а снизу – осью Ox (рис. 1), вычисляется по формуле:
, а снизу – осью Ox (рис. 1), вычисляется по формуле:
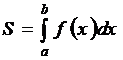 . (12.6)
. (12.6)
Площадь фигуры, ограниченной сверху и снизу соответственно линиями 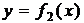 и
и 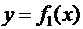 , слева и справа прямыми
, слева и справа прямыми 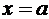 и
и 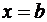 , определяется по формуле:
, определяется по формуле:
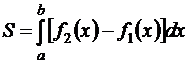 . (12.7)
. (12.7)
Площадь криволинейной трапеции, прилежащей к оси Oy, вычисляется по формуле:
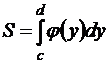 . (12.8)
. (12.8)
ТЕМА ЛЕКЦИИ № 9: Дифференциальные уравнения первого порядка с разделяющимися переменными. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Обыкновенным дифференциальным уравнением (ДУ) называется некоторая функциональная зависимость, содержащая переменную 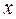 , искомую функцию
, искомую функцию 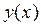 и её производные, то есть
и её производные, то есть
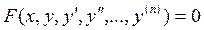 . (13.1)
. (13.1)
Наивысший порядок производной, входящей в ДУ, называется порядкомэтого уравнения. Тогда (13.1) – ДУ 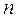 -го порядка.
-го порядка.
Следовательно, ДУ 1-го порядка имеет вид: 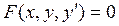 . (13.2)
. (13.2)
Если из (13.2) выразить 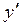 , то получим ДУ 1-го порядка, разрешенное относительно производной:
, то получим ДУ 1-го порядка, разрешенное относительно производной: 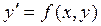 . (13.3)
. (13.3)
Решением ДУ называется такая функция 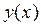 , которая, будучи подставленной вместе со всеми своими производными до
, которая, будучи подставленной вместе со всеми своими производными до 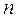 -го порядка в уравнение, обращает его в тождество.
-го порядка в уравнение, обращает его в тождество.
Методом решения ДУ является интегрирование, а график решения ДУ называется интегральной кривой.
Процесс интегрирования для ДУ 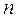 -го порядка повторяется
-го порядка повторяется 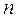 раз. Следовательно, искомое решение будет содержать ровно
раз. Следовательно, искомое решение будет содержать ровно 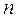 констант интегрирования. Решение ДУ, содержащее константы интегрирования
констант интегрирования. Решение ДУ, содержащее константы интегрирования 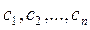 , называется общим решением ДУ:.
, называется общим решением ДУ:. 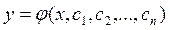 (13.4)
(13.4)
Если данное решение получено в неявном виде 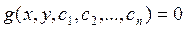 , то оно называется общим интегралом.
, то оно называется общим интегралом.
Для ДУ 1-го порядка общий интеграл записывается в виде 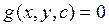 , а общее решение
, а общее решение 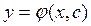 . (13.5)
. (13.5)
Решение ДУ, получаемое из общего решения при конкретных значениях констант интегрирования, называется его частным решением (частным интегралом).
Решение ДУ, не получаемое из общего решения ни при каких значениях константы 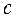 , называется особым.
, называется особым.
С геометрической точки зрения общее решение ДУ 1-го порядка 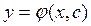 есть семейство интегральных кривых на плоскости
есть семейство интегральных кривых на плоскости 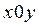 ; особое решение представляет собой огибающую интегрального семейства; частное решение
; особое решение представляет собой огибающую интегрального семейства; частное решение 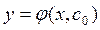 при
при 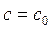 – одна кривая из этого семейства, походящая через точку
– одна кривая из этого семейства, походящая через точку 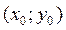 . Задать эту точку означает задать для данного дифференциального уравнения начальные условия:
. Задать эту точку означает задать для данного дифференциального уравнения начальные условия:
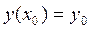 или
или 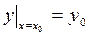 . (13.6)
. (13.6)
Геометрически задание начальных условий подразумевает выделение из всего семейства интегральных кривых выделение именно той кривой, которая проходит через точку с координатами 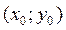 .
.
Если составить систему, состоящую из самого ДУ и заданных для него начальных условий, то получим задачу Коши для данного ДУ. Запишем задачу Коши для ДУ 1-го порядка:
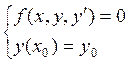 . (13.7)
. (13.7)
Аналогично можно записать задачи Коши для ДУ 2-го и 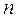 -го порядка соответственно:
-го порядка соответственно:
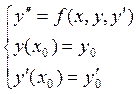 , (13.8)
, (13.8)
………………………..
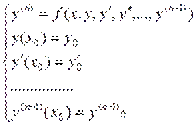 . (13.9)
. (13.9)
Для того чтобы найти частное решение ДУ, удовлетворяющее заданным начальным условиям, необходимо:
1) проинтегрировав ДУ, найти его общее решение (общий интеграл);
2) в общее решение (общий интеграл) подставить заданные начальные условия, получая при этом уравнение (систему уравнений) относительно констант интегрирования 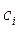 , где
, где 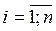 ;
;
3) решить уравнение относительно 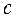 или систему уравнений относительно
или систему уравнений относительно 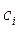 ;
;
4) найденные 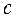 или
или 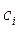 подставить в общее решение ДУ 1-го или n-го порядка соответственно.
подставить в общее решение ДУ 1-го или n-го порядка соответственно.
Пример.Найти частное решение ДУ 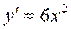 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 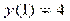 .
.
Решение. Учитывая, что , имеем или 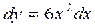 . Проинтегрировав данное уравнение
. Проинтегрировав данное уравнение 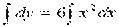 , получим общее решение
, получим общее решение 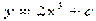 . Подставим в него начальные условия
. Подставим в него начальные условия 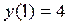 :
:
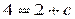 или
или 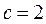 . Данное значение константы подставим в общее решение:
. Данное значение константы подставим в общее решение: 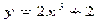 – искомое частное решение
– искомое частное решение 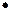
Дифференциальные уравнения с разделяющимися переменными
Пусть дано дифференциальное уравнение первого порядка вида
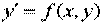 , (13.10)
, (13.10)
причем правая часть этого уравнения представляет собой произведение функций, каждая из которых зависит только от одной переменной: либо от переменной 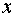 , либо от переменной
, либо от переменной 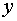
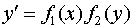 (13.11)
(13.11)
При этом возможен случай, когда какая-то одна из функций 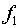 и
и 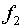 или обе – константы.
или обе – константы.
Запишем производную в виде 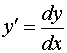 и домножим обе части уравнения (13.11) на
и домножим обе части уравнения (13.11) на 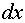 , получим
, получим
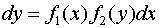 .
.
Следующим шагом попытаемся разделить переменные, то есть сделать так, чтобы каждая часть уравнения содержала бы функции и дифференциалы одной и той же переменной. Этого можно достичь путем деления обеих частей уравнения на 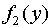 :
:
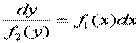 (13.12)
(13.12)
Данное уравнение называется уравнением с разделенными переменными, которое можно проинтегрировать, получив тем самым общее решение (общий интеграл) уравнения (13.11)
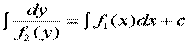 .
.
Замечание 1. При делении на 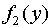 мы можем потерять отдельные особые решения, обращающие функцию
мы можем потерять отдельные особые решения, обращающие функцию 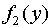 в нуль. Если же в уравнении (13.11) функция
в нуль. Если же в уравнении (13.11) функция 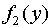 тождественно равна нулю, то очевидно, что решением уравнения
тождественно равна нулю, то очевидно, что решением уравнения 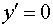 будет некоторая константа
будет некоторая константа 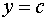 .
.
Замечание 2. В некоторых случаях полученные интегралы не берутся в элементарных функциях, тем не менее, если существуют какие-то другие способы вычисления полученных интегралов, уравнение считается проинтегрированным.
Уравнение с разделяющимися переменными кроме виды (13.11) может иметь вид
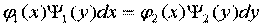 (13.13)
(13.13)
Привести такое уравнение к уравнению с разделенными переменными можно делением обеих частей равенства на произведение 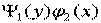 :
:
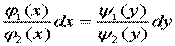
Полученное равенство можно интегрировать.
