Свойства неограниченного интеграла

1. 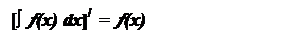Производная неопределенного интеграла равна подинтеральной функции, т.е.

2. Дифференциал неопределенного интеграла равен подинтегральному выражению, т.е.

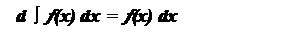
3. Неопределеннный интеграл от дифференциала некоторой функции F(x) равен самой функции с точностью до производной постоянной C

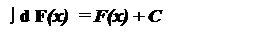
4. Постоянный множитель можно выносить за знак неопределенного интеграла,

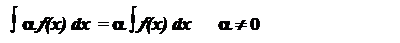
5. Интеграл от суммы нескольких функций равен сумме интегралов каждой функции

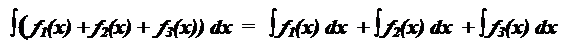
таблица интегралов от простейших функций:

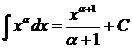при a ¹ –1

При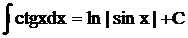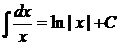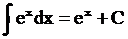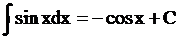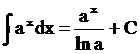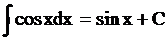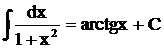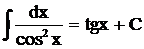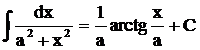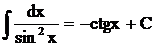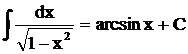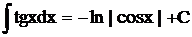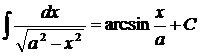ведем еще две формулы, справедливость которых можно проверить дифференцированием.

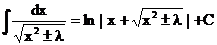
Интегрирование в случаях, когда удается сразу воспользоваться табличными интегралами, называют непосредственным. Чаще подинтегральную функцию приходится преобразовывать, чтобы свести исходный интеграл к одному или нескольким табличным.

Один из эффективных приемов – метод подстановки: в интеграле вида òf(x)dxделают замену переменной, положив x = j(t)(j(t) – непрерывная функция с непрерывной производной, имеющая обратную функцию). Тогда dx = j`(t)dt и òf(x)dx = òf(j(t))j`(t)dt. Подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х (возвращение к исходной переменной). Функцию j(t) следует выбирать так, чтобы вычисление интеграла в правой части было максимально простым.

Интегрирование по частям.Если u и v дифференцируемые функции от х, то d(uv) = vdu + udv откуда, интегрируя, получим

uv = òvdu + òudvиòudv = uv – òvdu

Это соотношение называют формулой интегрирования по частям.

Подинтегральное выражение "разбивают на части" - u и dv, подбирая их так, чтобы òvdu был табличным или более простым, чем исходный.

Отметим, что при нахождении v по dv произвольную постоянную без потери общности полагают равной нулю.

тема 6. Определенный интеграл

Пусть функция у = ¦(x) определена на отрезке [ a,b ]и a < b.

Разобьем этот отрезок на n произвольных частей точками

a = x₀ < x₁ < x₂ < x₃ …. < x_n = b

В каждом из частичных промежутков (x₀,x₁), (x₁,x₂), (x₂,x₃),…., (x_n,x_n+1) возьмем по точке: в промежутке (x₀,x₁) точку b₁ , в промежутке (x₁,x₂) точку b₂ и так далее.

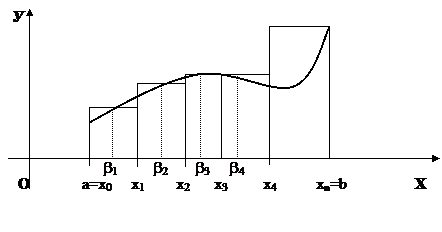
Составим сумму:

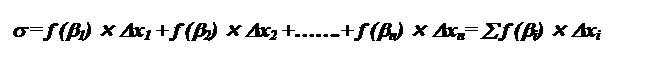- эту сумму называют интегральной суммой

Геометрический смысл интегральной суммы: это сумма площадей прямоугольников с основанием Dx_i, это площадь криволинейной трапеции.

Определение: предел, к которому стремиться сумма s (сигма), когда наибольшая из длин всех частичных промежутков стремится к нулю, называется определенным интегралом функции ¦(x). Концы [ a,b ]данного промежутка называются пределами интегрирования: a – нижним, b – верхним.

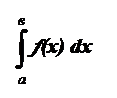Определенный интеграл обозначается