Векторы. Линейные операции над векторами
Элементы векторной алгебры
Векторы. Линейные операции над векторами
Понятие вектора
Направленным отрезком называется отрезок, у которого указаны начало и конец. Обозначение: 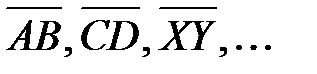
Вектором называется направленный отрезок. Обозначение: 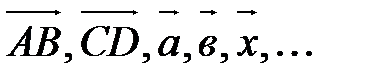 (рис. 1).
(рис. 1).
| А |
| D |
| C |
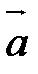 |
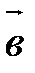 |
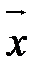 |
| Рис. 1 |
Вектор называется нулевым, если его начало и конец совпадают. Обозначение: 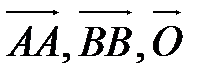 .
.
Векторы 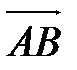 и
и 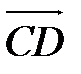 называются сонаправленными (противоположно направленными), если лучи [AB) и [CD)сонаправлены (противоположно направлены). Обозначение:
называются сонаправленными (противоположно направленными), если лучи [AB) и [CD)сонаправлены (противоположно направлены). Обозначение: 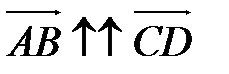 (
( 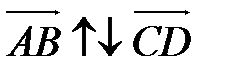 ).
).
На рис. 2 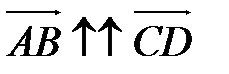 ,
, 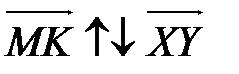 .
.
| А |
| В |
| С |
| D |
| K |
| M |
| X |
| Y |
| Рис. 2 |
Векторы 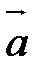 и
и 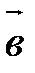 называютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:
называютсяколлинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение: 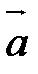 ||
|| 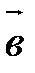 .
.
Нулевой вектор считается коллинеарным любому вектору.
Векторы 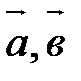 и
и 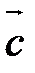 называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
Длиной вектора называется расстояние между его началом и концом. Обозначение длины вектора 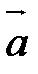 :
:  .
.
Длина нулевого вектора равна 0, т.е. 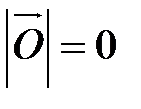 .
.
Вектор называется единичным, если его длина равна единице.
В пространстве существует бесконечное множество единичных векторов.
Два вектора называются равными, если они сонаправлены и длины их равны. Обозначение: 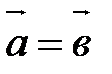 .
.
Два вектора называются противоположными, если они противоположно направлены и длины их равны.
Вектор, противоположный вектору 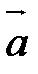 , обозначается
, обозначается 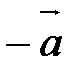 .
.
Откладыванием вектора 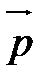 от точки А называется процесс построения такой точки М, что
от точки А называется процесс построения такой точки М, что 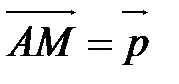 .
.
| В |
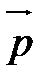 и точка А. Сначала строят луч
и точка А. Сначала строят луч 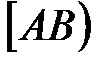 , исходящий из точки А и сонаправленный с вектором
, исходящий из точки А и сонаправленный с вектором 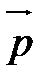 (рис. 3). Затем на луче
(рис. 3). Затем на луче 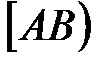 откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора
откладывают с помощью циркуля отрезок АМ, длина которого равна длине вектора 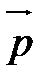 . Вектор
. Вектор 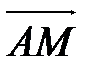 - искомый, т.е.
- искомый, т.е. 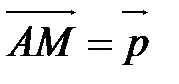 .
.
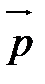 |
| А |
| М |
| Рис. 3 |
Сложение и вычитание векторов
Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число.
Результатом сложения векторов является их сумма. Сумма векторов  и
и 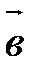 обозначается
обозначается 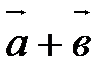 .
.
Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма.
Правило треугольника
Чтобы сложить векторы  и
и 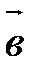 , надо взять произвольную точку и от нее отложить последовательно сначала вектор
, надо взять произвольную точку и от нее отложить последовательно сначала вектор  , затем вектор
, затем вектор 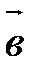 . Вектор, начало которого совпадает с началом вектора
. Вектор, начало которого совпадает с началом вектора  (т.е. первого вектора), а конец – с концом вектора
(т.е. первого вектора), а конец – с концом вектора 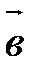 (т.е. второго вектора), есть искомая сумма. На рис. 4
(т.е. второго вектора), есть искомая сумма. На рис. 4 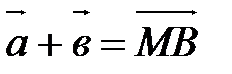 .
.
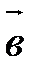 |
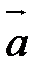 |
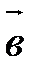 |
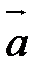 |
| М |
| В |
| Рис. 4 |
По правилу треугольника можно складывать любые векторы.
Коротко правило треугольника можно записать так:
для любых трех точек А,В и С 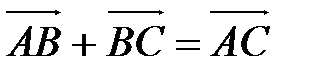 .
.
Правило параллелограмма
Чтобы сложить векторы  и
и 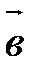 , надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что
, надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что 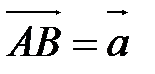 и
и 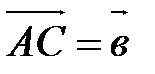 , и достроить полученную фигуру до параллелограмма
, и достроить полученную фигуру до параллелограмма 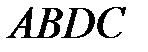 . Вектор
. Вектор 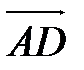 - искомая сумма (рис. 5).
- искомая сумма (рис. 5).
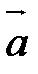 |
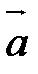 |
 |
 |
| А |
| С |
| В |
| D |
| Рис. 5 |
По правилу параллелограмма можно складывать тольконеколлинеарные векторы.
Свойства сложения векторов:
10. 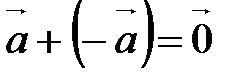
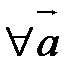 .
.
20. 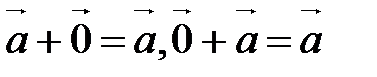
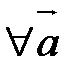 .
.
30. 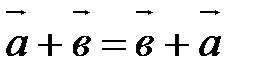
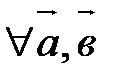 .
.
40. 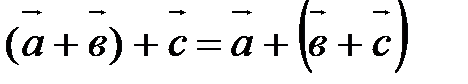
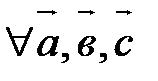 .
.
Суммой трех векторов 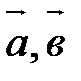 и
и 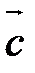 называется вектор
называется вектор 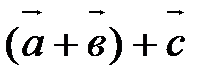 . Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде
. Учитывая свойство 40, скобки можно опустить и обозначать сумму в виде 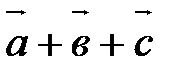 .
.
Суммой nвекторов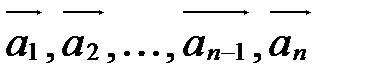 называется вектор
называется вектор 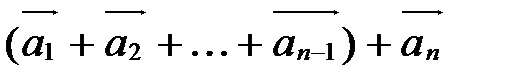 и обозначается так:
и обозначается так: 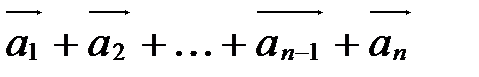 .
.
При построении суммы n векторов пользуются правилом многоугольника.
Правило многоугольника
Чтобы найти сумму nвекторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.
Разностью векторов  и
и 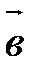 называется такой вектор
называется такой вектор 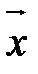 , что
, что 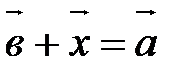 . Разность – это результат вычитания векторов. Разность векторов
. Разность – это результат вычитания векторов. Разность векторов  и
и 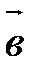 обозначается так:
обозначается так: 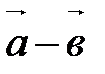 .
.
Умножение вектора на число
Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.
Произведением вектора  на действительное число a называется вектор
на действительное число a называется вектор 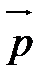 , обозначаемый через
, обозначаемый через 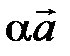 и удовлетворяющий двум условиям:
и удовлетворяющий двум условиям:
1) его длина 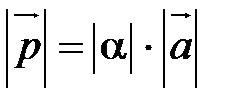 ;
;
2) если a  0, то
0, то 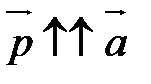 ; если
; если 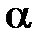 <0, то
<0, то 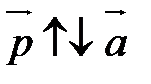 .
.
Алгоритм построения произведения вектора  числоa таков.
числоa таков.
Берем произвольную точку М. Проводим луч 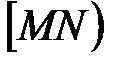 ,сонаправленный с вектором
,сонаправленный с вектором 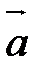 , если a
, если a  0, и противоположно направленный с вектором
0, и противоположно направленный с вектором 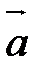 , если
, если 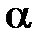 <0. На луче
<0. На луче 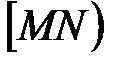 от начала М откладываем отрезок MP, длина которого в
от начала М откладываем отрезок MP, длина которого в 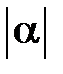 раз больше длины вектора
раз больше длины вектора  .Вектор
.Вектор 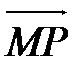 - искомый вектор
- искомый вектор 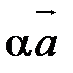 .
.
Продемонстрируем этот алгоритм на конкретном примере. Построим вектор 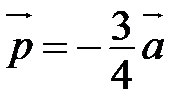 , если
, если  - данный вектор.
- данный вектор.
Возьмем произвольную точку А. Так как 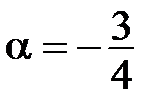 <0, то проводим луч
<0, то проводим луч 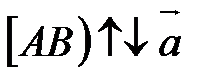 (рис. 7). На луче
(рис. 7). На луче 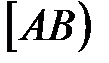 строим такую точку С, что
строим такую точку С, что 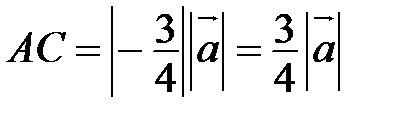 . Тогда
. Тогда 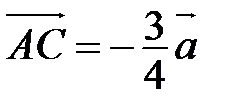 - искомый вектор.
- искомый вектор.
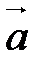 |
| А |
| С |
| В |
| Рис. 7 |
Примеры
1. Система векторов 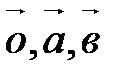 линейно зависима, т.к. если возьмем
линейно зависима, т.к. если возьмем 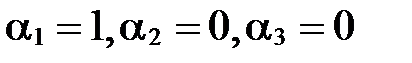 , то получим, что
, то получим, что 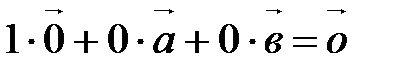 , т.е. существуют такие действительные числа
, т.е. существуют такие действительные числа 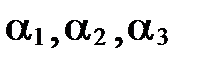 , не все равные 0 одновременно (
, не все равные 0 одновременно ( 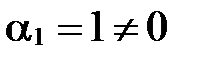 ), что выполняется равенство
), что выполняется равенство 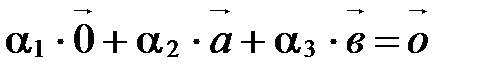 .
.
2. Система двух неколлинеарных векторов  и
и 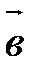 линейно независима, т.к. сумма двух неколлинеарных векторов
линейно независима, т.к. сумма двух неколлинеарных векторов 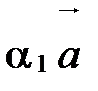 и
и 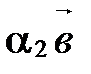 равна нулевому вектору
равна нулевому вектору 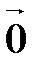 только при
только при 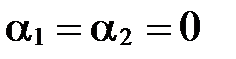 .
.
Базис. Координаты вектора
И их свойства
Множество всех векторов, на котором введена операция сложения векторов, удовлетворяющая свойствам
10. 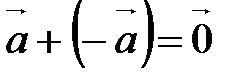 ;
;
20. 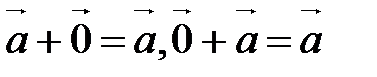 ;
;
30. 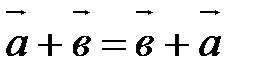 ;
;
40. 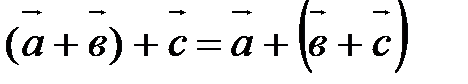 ,
,
и операция умножения вектора на число, удовлетворяющая свойствам
10. 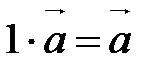 ,
, 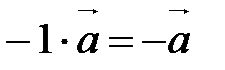 ;
;
20. 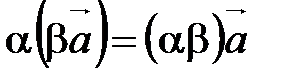 ;
;
30. 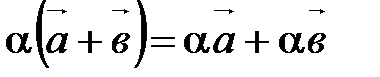 ;
;
40. 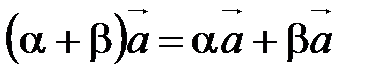 ,
,
называется векторным пространством и обозначается через V.
Базисом векторного пространства называется система векторов, заданных в определенном порядке, которая удовлетворяет условиям:
1) система линейно независима;
2) любой вектор пространства является линейной комбинацией данной системы векторов.
Число векторов базиса называется размерностью векторного пространства.
Выяснить, чему равна размерность векторного пространства V, позволяют следующие две теоремы, которые приведем без доказательства:
Теорема 1. Любая система трех некомпланарных векторов, взятых в определенном порядке, образует базис векторного пространства.
А может ли базис пространства V состоять меньше, чем из трех векторов? Больше, чем из трех векторов? Оказывается, нет, так как справедлива
Теорема 2. Любой базис векторного пространства V состоит из трех векторов.
Эти теоремы можно доказать, пользуясь теоремами о коллинеарных и компланарных векторах и свойствами 20 - 70линейно зависимой системы векторов.
Из теорем 1 и 2 следует, что размерность векторного пространства V равна 3, поэтому оно называется трехмерным векторным пространством.
Базис, состоящий из векторов 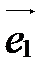 ,
, 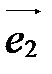 и
и 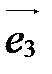 , обозначается так:
, обозначается так: 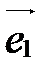 ,
, 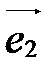 ,
, 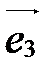 или
или 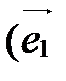 ,
, 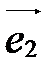 ,
, 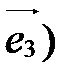 . Векторы
. Векторы 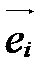 ,
, 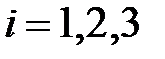 , называются базисными векторами:
, называются базисными векторами: 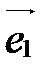 -первый базисный вектор,
-первый базисный вектор, 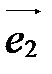 -второй,
-второй, 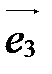 - третий.
- третий.
Пусть 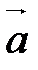 - произвольный вектор пространства V,
- произвольный вектор пространства V, 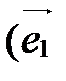 ,
, 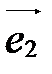 ,
, 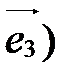 - базис векторного пространства V.
- базис векторного пространства V.
Из теоремы 1 следует, что вектор 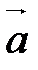 можно разложить по базисным векторам
можно разложить по базисным векторам 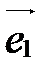 ,
, 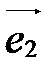 ,
, 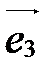 , т.е. существуют такие действительные числа
, т.е. существуют такие действительные числа 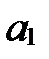 ,
, 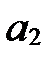 ,
, 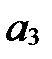 , что
, что
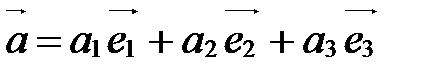 .
.
Коэффициенты 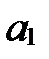 ,
, 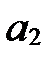 ,
, 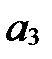 в этом разложении называются координатами вектора
в этом разложении называются координатами вектора 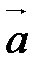 в базисе
в базисе 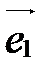 ,
, 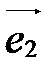 ,
, 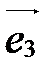 :
: 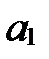 - первая координата,
- первая координата, 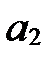 - вторая,
- вторая, 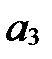 - третья.
- третья.
Обозначают это так: 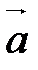 (
( 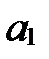 ;
; 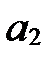 ;
; 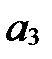 )
) 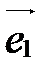 ,
, 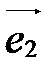 ,
, 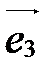 .
.
Когда ясно, о каком базисе идет речь, пишут так: 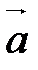 (
( 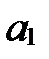 ;
; 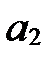 ;
; 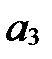 ).
).
Свойства координат векторов
10. Нулевой вектор в любом базисе имеет нулевые координаты: 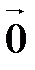 (0;0;0).
(0;0;0).
□ Разложим 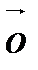 по векторам базиса
по векторам базиса 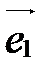 ,
, 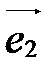 ,
, 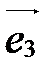 :
:
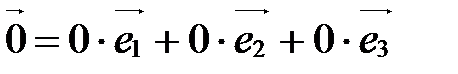 .
.
Следовательно, 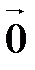 (0;0;0)
(0;0;0) 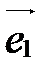 ,
, 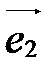 ,
, 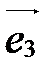 .■
.■
20. Если 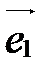 ,
, 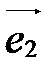 ,
, 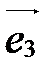 - базис пространства V, то
- базис пространства V, то 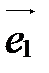 (1;0;0),
(1;0;0), 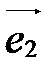 (0;1;0),
(0;1;0), 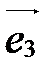 (0;0;1).
(0;0;1).
□ 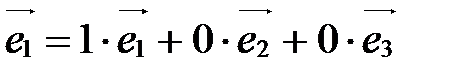
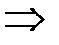
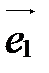 (1;0;0);
(1;0;0);
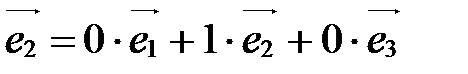
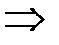
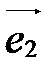 (0;1;0);
(0;1;0);
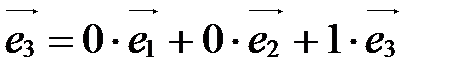
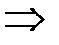
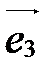 (0;0;1). ■
(0;0;1). ■
30. Если 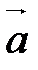 (
( 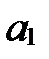 ;
; 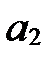 ;
; 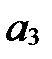 ),
), 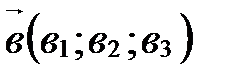 в базисе
в базисе 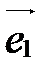 ,
, 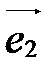 ,
, 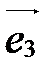 , а
, а 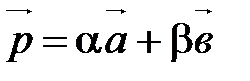 , то
, то
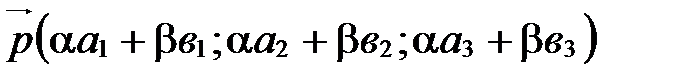
в базисе 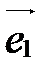 ,
, 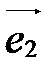 ,
, 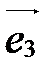 (координаты линейной комбинации векторов равны линейным комбинациям их соответствующих координат).
(координаты линейной комбинации векторов равны линейным комбинациям их соответствующих координат).
□ По определению координат вектора
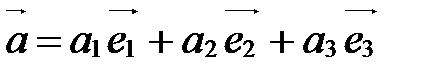 ,
, 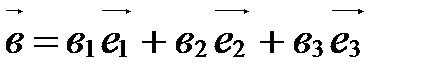 .
.
Тогда 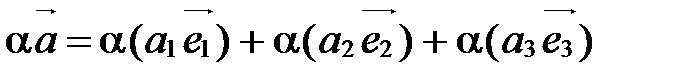 ,
, 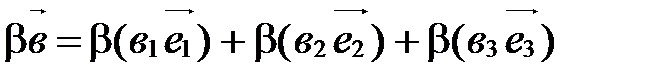 .
.
Сложим почленно эти равенства и воспользуемся свойствами сложения векторов и умножения вектора на число:
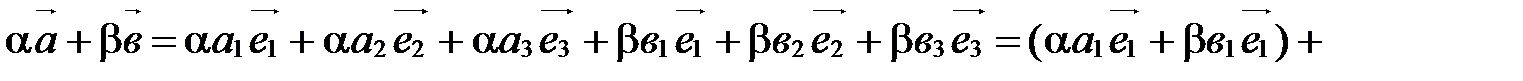
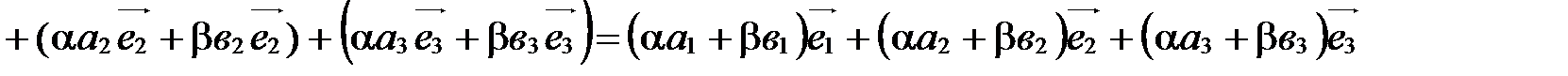 .
.
По определению координат вектора
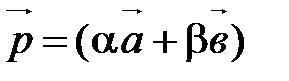
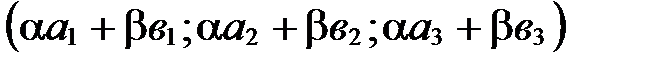 . ■
. ■
Из свойства 30 получаем следствия:
Следствие 1. Каждая координата суммы (разности) двух векторов равна сумме (разности) соответствующих координат этих векторов.
Следствие 2. При умножении вектора на число каждая его координата умножается на это число.
□ Чтобы доказать справедливость следствия 1, надо в свойстве 30 взять сначала a=b=1, а затем a=1, b=-1. Для доказательства следствия 2 полагаем b=0. ■
40. Векторы равны тогда и только тогда, когда равны их соответствующие координаты: 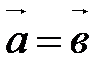

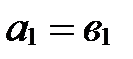 ,
, 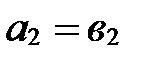 ,
, 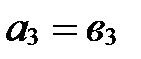 .
.
50. Пусть 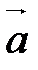 (
( 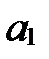 ;
; 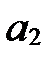 ;
; 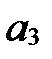 ),
), 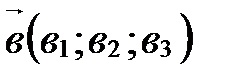 ,
, 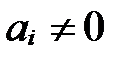 и
и 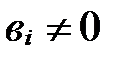 , i=1, 2, 3. Векторы
, i=1, 2, 3. Векторы 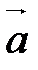 и
и 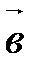 коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
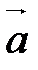 ||
|| 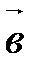

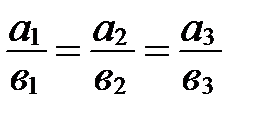 .
.
Пусть 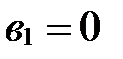 . Тогда
. Тогда
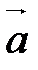 ||
|| 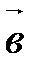

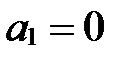 и
и 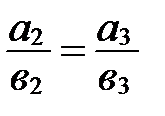 .
.
Если же 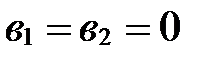 , то
, то
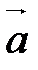 ||
|| 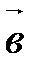

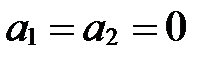 , а
, а 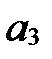 и
и 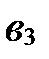 - любые.
- любые.
Частным случаем произвольного базиса является ортонормированный базис. Его удобно использовать при решении метрических задач (т.е. задач, связанных с вычислением длин отрезков (векторов) и величин углов).
| Е1 |
| Е3 |
| О |
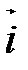 |
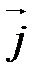 |
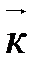 |
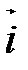 ,
, 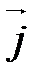 ,
, 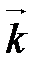 называется ортонормированным, если его векторы удовлетворяют двум условиям:
называется ортонормированным, если его векторы удовлетворяют двум условиям: 1) 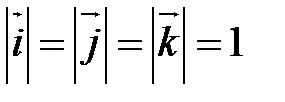 ;
;
| Рис. 8 |
| Е2 |
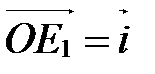 ,
, 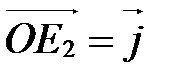 ,
, 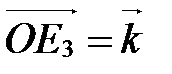 (рис. 8), то углы
(рис. 8), то углы 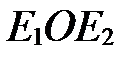 ,
, 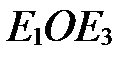 и
и 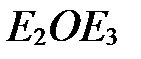 - прямые.
- прямые.
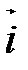 |
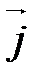 |
| Рис. 9 |
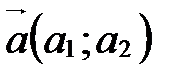 . Ортонормированный базис выглядит так:
. Ортонормированный базис выглядит так: 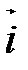 ,
, 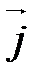 (рис. 9).
(рис. 9). Геометрические свойства
Алгебраические свойства
Приложение скалярного произведения
Геометрические свойства
Алгебраические свойства
Геометрические свойства
Алгебраические свойства
Трех векторов
Смешанное произведение векторов применяется:
1. Для выяснения компланарности трех векторов:
векторы 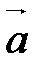 ,
, 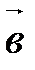 ,
, 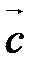 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда 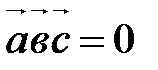 .
.
2. Для вычисления объема параллелепипеда: 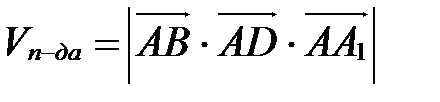 (рис. 28).
(рис. 28).
| Рис. 28 |
| Рис. 29 |
| А1 |
| D1 |
| С1 |
| В1 |
| D |
| С |
| В |
| А |
| А1 |
| В1 |
| С1 |
| А |
| В |
| С |
| Рис. 30 |
| D |
| А |
| В |
| С |
3. Для вычисления объема треугольной призмы:
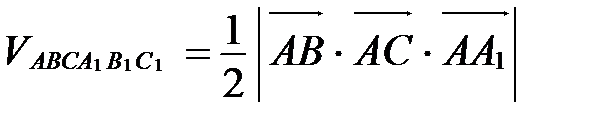 (рис. 29).
(рис. 29).
4. Для вычисления объема тетраэдра (треугольной пирамиды):
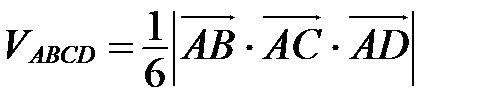 (рис. 30).
(рис. 30).
Задания для самостоятельной работы
1. Вычислите 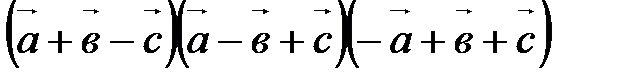 , если
, если 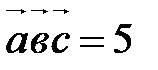 .
.
2. Докажите, что если 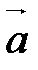 ||
|| 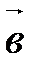 , то
, то 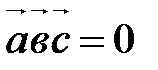 .
.
3. Выясните, какой является тройка векторов 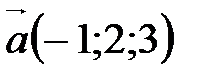 ,
, 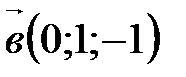 ,
, 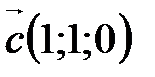 (левой или правой).
(левой или правой).
4. Докажите, что векторы 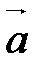 ,
, 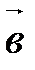 ,
, 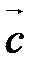 , удовлетворяющие условию
, удовлетворяющие условию 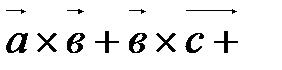
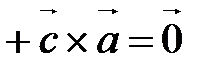 ,компланарны.
,компланарны.
5. Найдите объем треугольной призмы АВСА1В1С1, если 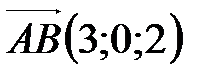 ,
, 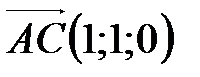 ,
, 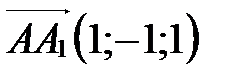 .
.
6. Найдите объем тетраэдра ABCD, если 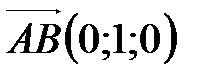 ,
, 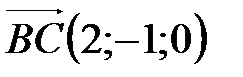 ,
, 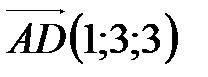 .
.
Метод координат
Системы координат
Систем координат
| О |
 |
 |
 |
| Рис. 31 |
| О |
 |
 |
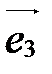 |
| х |
| у |
| z |
| Рис. 32 |
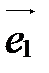 ,
, 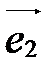 ,
, 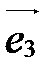 в пространстве, называется аффинной системой координат в пространстве и обозначается
в пространстве, называется аффинной системой координат в пространстве и обозначается 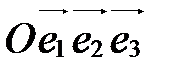 или
или 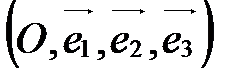 (рис. 31).
(рис. 31). Точка О называется началом координат, векторы 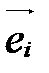 ,
, 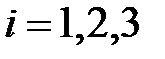 , - координатными векторами:
, - координатными векторами: 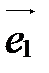 - первый координатный вектор,
- первый координатный вектор, 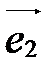 - второй,
- второй,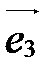 - третий.
- третий.
Направленные прямые, на которых положительное направление определяется базисными векторами и которые проходят через точку О, называются координатными осями:
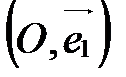 - ось абсцисс;
- ось абсцисс;
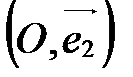 - ось ординат;
- ось ординат;
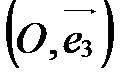 - ось аппликат (рис. 32).
- ось аппликат (рис. 32).
Оси абсцисс, ординат и аппликат обозначаются и так: Ох, Оу, Оz.
Плоскости, определяемые осями Ох и Оу, Оу и Оz, Ох и Оz, называются координатными плоскостями и обозначаются Оху, Оуz, Oxz, а систему координат 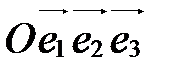 иногда обозначают Oxyz.
иногда обозначают Oxyz.
| Рис. 33 |
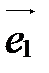 |
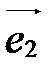 |
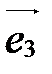 |
| О |
| М |
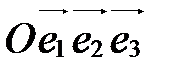 - аффинная система координат, М – произвольная точка пространства. Вектор
- аффинная система координат, М – произвольная точка пространства. Вектор 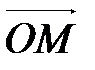 называетсярадиус-вектором точки М относительно точки О(рис. 33).
называетсярадиус-вектором точки М относительно точки О(рис. 33). Понятие координат точки вводится на основе понятия координат вектора.
Координатами точки М в системе координат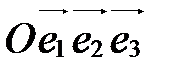 называются координаты ее радиус-вектора
называются координаты ее радиус-вектора 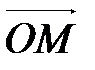 в базисе
в базисе 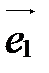 ,
, 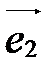 ,
, 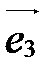 .
.
Обозначение 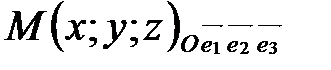 или просто М(х;у;z): х – абсцисса точки М, у – ордината, z– аппликата.
или просто М(х;у;z): х – абсцисса точки М, у – ордината, z– аппликата.
Если в пространстве задана аффинная система координат, то устанавливается взаимно однозначное соответствие между точками пространства и упорядоченными тройками (х;у;z) действительных чисел.
Рассмотрим особенности расположения точки относительно аффинной системы координат, если некоторые ее координаты являются нулевыми. Пусть М(х;у;z).
1) Если z=0, то М(х;у;0)Þ 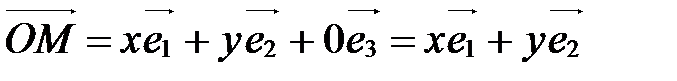 Þ
Þ 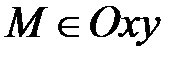 . Верно и обратное:
. Верно и обратное: 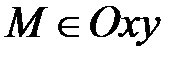 Þz=0.
Þz=0.
2) Докажите самостоятельно, что если у=0, то  , и наоборот, если
, и наоборот, если  , то у=0.
, то у=0.
3) Докажите самостоятельно, что если х=0, то 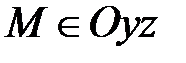 , и наоборот, если
, и наоборот, если 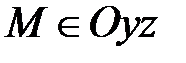 , то х=0.
, то х=0.
4) Если z=0 и у=0, то 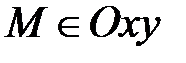 и
и  Þ
Þ 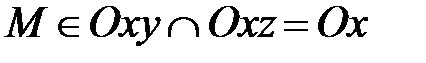 Þ
Þ 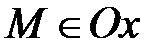 . Верно и обратное:
. Верно и обратное: 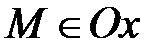 Þz=0 и у=0.
Þz=0 и у=0.
Докажите самостоятельно, что:
5) Если х=0 и у=0, то 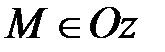 и наоборот, если
и наоборот, если 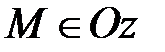 , то х=0 и у=0.
, то х=0 и у=0.
6) Если х=0 и z=0, то 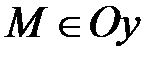 и наоборот, если
и наоборот, если 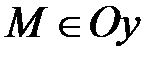 , то х=0 и z=0.
, то х=0 и z=0.
7) Так как 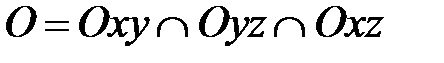 , то из пунктов 1) – 3) следует, что О(0;0;0) в системе координат
, то из пунктов 1) – 3) следует, что О(0;0;0) в системе координат 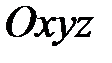 .
.
Чтобы построить точку М(х;у;z) по ее координатам в системе координат 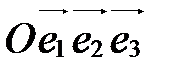 , надо сначала построить точку М1(х;0;0), затем точку М2(х;у;0), а затем точку М(х;у;z). Процесс построения этих точек показан на рис. 34. Ломаная ОМ1М2М называется координатной ломаной точки М.
, надо сначала построить точку М1(х;0;0), затем точку М2(х;у;0), а затем точку М(х;у;z). Процесс построения этих точек показан на рис. 34. Ломаная ОМ1М2М называется координатной ломаной точки М.
| М1 |
| М |
| М2 |
| О |
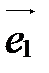 |
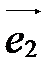 |
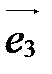 |
| Рис. 34 |
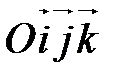 или
или 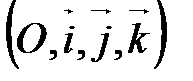 , где
, где 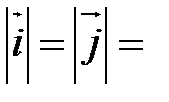
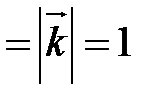 ,
, 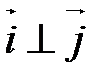 ,
, 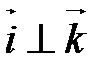 и
и 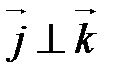 .
.
Прямоугольная декартова система координат является частным случаем аффинной.
Замечание. На плоскости аффинная система координат состоит из точки О (начала координат) и двух базисных векторов 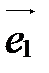 и
и 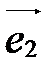 (координатных векторов) (рис. 35). Поэтому в системе координат на плоскости любая точка имеет две координаты
(координатных векторов) (рис. 35). Поэтому в системе координат на плоскости любая точка имеет две координаты 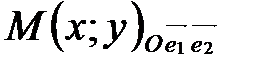 . Прямоугольная декартова система координат на плоскости изображена на рис. 36.
. Прямоугольная декартова система координат на плоскости изображена на рис. 36.
| О |
| О |
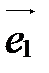 |
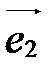 |
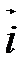 |
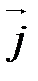 |
| Рис. 35 |
| Рис. 36 |
Основные аффинные задачи
1. Координаты вектора, заданного двумя точками.
Теорема 1. Если в аффинной системе координат 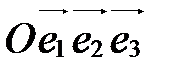
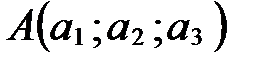 и
и 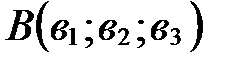 , то
, то 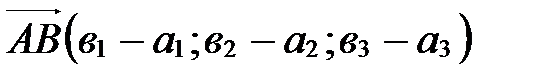 .
.
Представим вектор 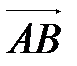 в виде разности векторов
в виде разности векторов 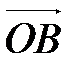 и
и 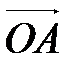 :
:
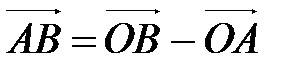 .
.
Так как 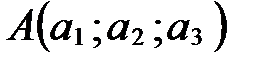 , то по определению координат точки
, то по определению координат точки 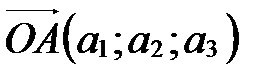 . Аналогично
. Аналогично 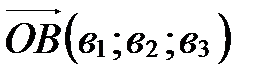 . Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор
. Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что вектор 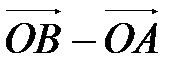 имеет координаты
имеет координаты 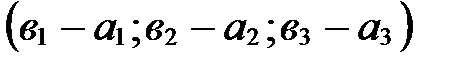 Þ
Þ 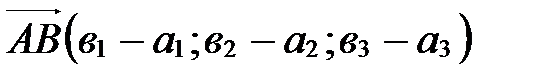 .
.
2. Деление отрезка в данном отношении.
Говорят, что точка М делит направленный отрезок 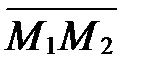 в отношении
в отношении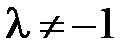 , если выполняется векторное равенство:
, если выполняется векторное равенство:
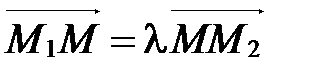 . (1)
. (1)
Число