Передаточная функция замкнутой САР равна

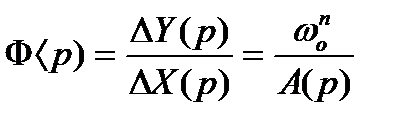
Переходные характеристики, соответствующие этому случаю, построены в нормированном виде на рис. 15 и по оси времени откладывается относительное время t = wt .

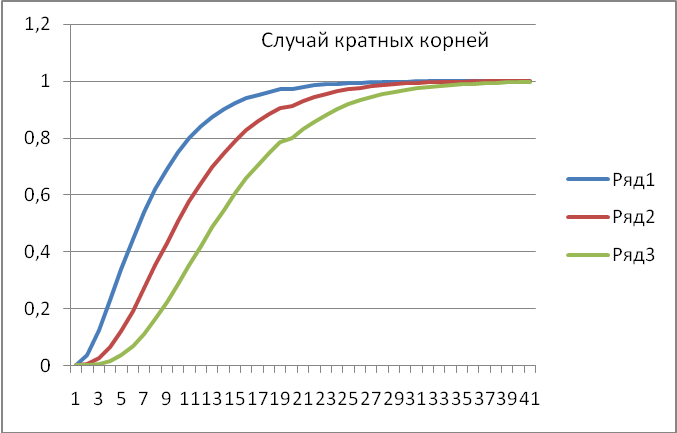
Рис. 15.График переходного процесса для настройки регулятора при равенстве корней характеристического уравнения

Оптимальный переходный процесс связан с минимизацией какого-либо оптимизирующего функционала, простейшим из которых является квадратичный

I₁ = ,

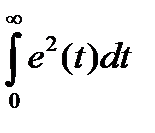позволяющий рассчитать регулятор на минимум среднеквадратичной ошибки. При этом характеристические уравнения замкнутой САР для n = 1 ÷ 4 имеют вид:

p + w₀

p² + w₀ p + w₀²

p³ + w₀ p² + 2 w₀² p +w₀³

p⁴ + w₀ p³+ 3 w₀² p² + 2 w₀³ p + w₀⁴

Переходные характеристики замкнутой САР, настроенной на минимум среднеквадратичной ошибки, построены на рис. 16.

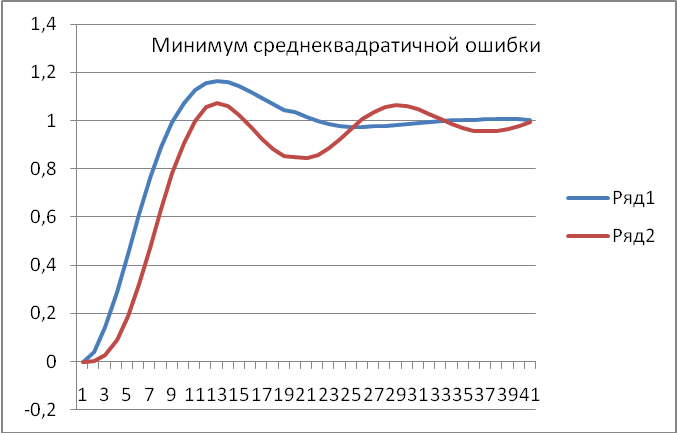Рис.16.График переходного процесса при настройке регулятора на минимум среднеквадратической ошибки.

Более сложный оптимизирующий функционал, который учитывает сходимость переходного процесса, для n = 1 ¸ 4 выглядит следующим образом:

n = 2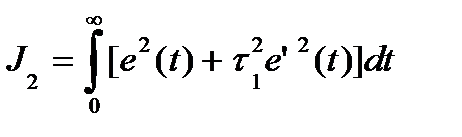

n = 3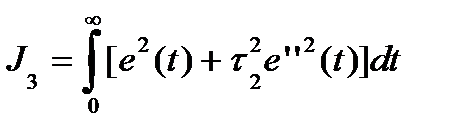

n = 4 ,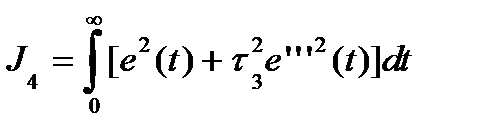

где t_i - весовые коэффициенты, имеющие размерность времени.

В этом случае корни характеристического уравнения на комплексной плоскости при одинаковости углов располагаются на полуокружности радиуса w₀. Впервые такое расположение корней было предложено Баттервортом и называется настройкой на оптимум по модулю. Характеристические уравнения замкнутой САР для n = 1 ¸ 4 имеют вид:

p + w₀

p² + 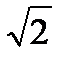w₀p +w₀²

p³ + 2w₀p² + 2 w₀²p + w₀³

p⁴ + 2,6w₀p³ + 3,4 w₀²p² + 2,6 w₀³p + w₀⁴

Переходные характеристики замкнутой САР с распределением корней с настройкой на оптимум по модулю построены на рис. 17 и по сравнению с характеристиками биномиальных форм имеют незначительную колебательность и меньшее время регулирования. Во многих случаях они соответствуют интуитивному представлению об оптимальном переходном процессе.

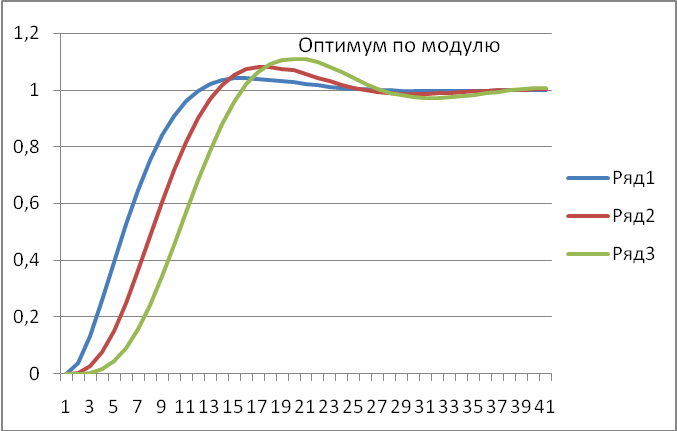
Рис.17. График переходного процесса при настройке регулятора на минимум среднеквадратической ошибки

Рассмотрим примеры расчета параметров регулятора для разных систем автоматического регулирования.

ПРИМЕР 1.

САУ частоты вращения двигателя постоянного тока, управляемого тиристорным преобразователем по цепи якоря.

Передаточная функция неизменяемой части системы W_н(p) равна

,

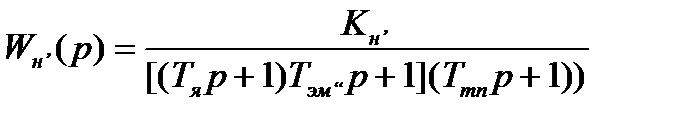
гдеК_н - коэффициент передачи неизменяемой части САР,

К_н = К_дК_тпК_тгК_п ,

К_д - коэффициент передачи двигателя,

К_тп - коэффициент передачи тиристорного преобразователя,

К_тг - коэффициент передачи тахогенератора,

К_п - коэффициент передачи потенциометра,

Т_я ,Т_эм ,Т_тп - постоянные времени якорной цепи и электромеханическая двигателя и тиристорного преобразователя.

Выбираем ПИД - регулятор для компенсации постоянных времени двигателя и введения астатизма в систему:

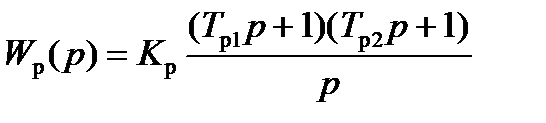
Тогда передаточная функция разомкнутой САР будет

W (p) = ,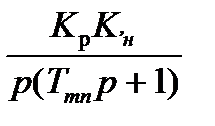

если Т_р1 = ,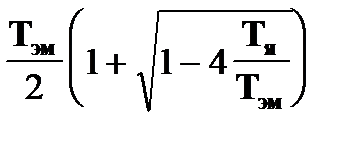

Т_р2 = .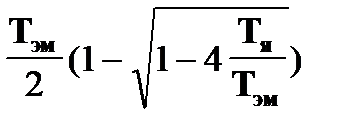

Передаточная функция замкнутой САР по управлению

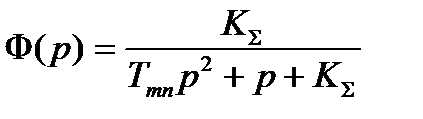
Характеристическое уравнение замкнутой САР

p² + A₁ w₀ p + w₀² = 0,

где A₁w₀ = 1/T_тп , w₀² = K_S /T_тп

1. Биномиальная стандартная форма переходной характеристики

p² + 2 w₀ p + w₀² = 0

Тогда 2w₀ = 1 / T_тп и w₀ = 1 / 2T_тп ,

поэтому К_S = 1 / 4T_тп и К_р = K_S / K_н

2. Переходная характеристика по минимуму среднеквадратичной ошибки

p² + w₀ p + w₀² = 0

где w₀ = 1 / Т_тп ; К_S = 1 / Т_тп ; К_р = К_S / К_н