Ускорения точек и угловые ускорения звеньев

Ускорения точек механизма определим методом планов. Ускорение точки А вычислим по формуле

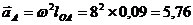м/с².

Примем длину вектора ускорения точки А на плане 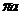= 50 мм, тогда масштаб будет равен:

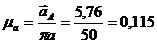м / (с мм).

Из произвольно выбранного по­люса параллельно кривошипу ОА и в направлении от А к О отложим отрезок .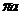

Составим исходные векторные уравнения для нахождения ускоре­ния

точки В:

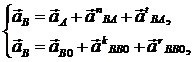
где 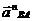нормальное ускорение, вектор которого направлен к центру

вращения, т. е. от точки В к точке А,

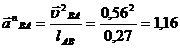м/с ;

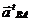- тангенциальное ускорение, направленное перпендикулярно отрезку АВ,

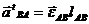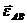( - угловое ускорение звена);

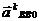- кориолисово ускорение, 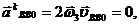так как ;

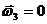- релятивное (относительное) ускорение точки В относительно точки В₀.

Из точки а плана ускорений отложим параллельно АВ и в сторону от В к А отрезок 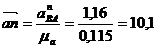мм.

В точки n восстановим перпендикуляр к отрезку 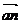— линию действия вектора тангенциального ускорения, а через полюс проведем прямую, параллель направляющей (х-х). Точка в пересечения перпендикуляра и этой прямой определяет положение конца вектора ускорения точки В.

Ускорение точки S шатуна устанавливается по правилам подобия.

Величины ускорений точек механизма найдем по формулам

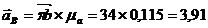м/с²,

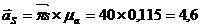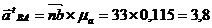м/с²,

м/с².

Угловое ускорение шатуна вычислим по формуле

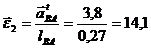рад/с.

Направления угловых ускорений определяем ориентацией векторов тангенциальных ускорений соответствующих точек звеньев, мысленно перенесенных в эти точки.

Силовой расчет механизма

Определим силы, действующие на звенья механизма, для расчета деталей на прочность, износ, а также мощность двигателя, установить тип и размеры подшипников и т.д.

Силы, действующие на звенья механизма

Вычислим силы, действующие на механизм, и расставим их в соответствующих точках.

Силы тяжести найдем по формуле

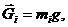
где m_i — масса соответствующего звена;

g — ускорение свободного падения, g =9,82 м/с² . При учебных

расчетах допускается принимать g = 10 м/с² .

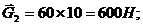
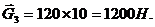
Силы тяжести прикладываются к центрам масс и направляются вертикально вниз.

Силы инерции звеньев вычислим из соотношения

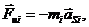
прикладываем к центрам масс и направим противоположно ускорениям соответствующих звеньев:

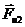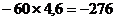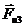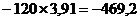= Н_,

= Н.

Моменты пары сил инерции вычисляются по формуле

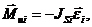
где J_Si — момент инерции i-го звена, кг • м².

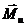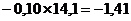= Н.

Сила полезных сопротивлений 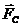=3000 Н.

Расчет группы 2—3

Кинетостатический расчет начинают со структурной группы, наиболее удаленной от ведущего звена. Отделим от механизма группу звеньев 2- 3и заменим связи реакциям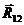и и .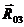

Разложим реакцию 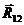нанормальную и тангенциальную составляющие.

Запишем уравнение моментов для звена 4 относительно очки В и определим :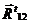

,

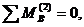
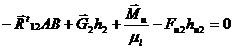где h₂, h_u2 — плечи действия сил (из чертежа), мм. Подставляем конкретные данные, получаем

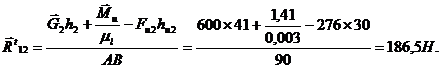
Запишем векторное уравнение равновесия для всей группы:

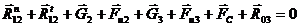
Это уравнение решим графически, для чего построим план сил в масштабе:

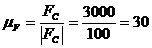Н/мм.

Тогда длины векторов будут равны:

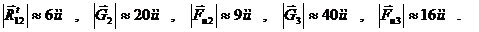
Построим многоуголь­ник плана сил в масштабе 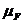, замкнув его известны­ми по направлениям векторам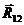и и 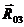. Искомые величины равны:

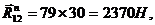
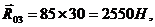
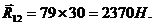
Для определения реак­ции 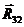запишем векторное уравнение равновесия для звена 2:

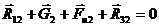
Из уравнения видно, что вектор 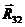является замыкающим в системе сил, действующих на звено 2. Тогда величина этой реакции

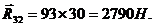
Таким образом, все неизвестные реакции в кинематических парах этой группы установлены.

Расчет ведущего звена

Ведущее звено 1 является механизмом 1-го класса и не относится к статически определимым группам ассура, т. е. оно не уравновешено.

Введем уравновешивающую силу F_У приложим ее в точку А и направим перпендикулярно к оси ОА. Кроме того, на ведущее звено действует реак­ция от звена 2 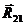и реакция от непод­вижного звена (стойки) .

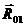Для определения величины уравно­вешивающей силы составим уравнение моментов относительно точки О:

,

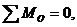
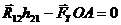откуда

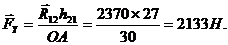
Запишем векторное уравнение рав­новесия для ведущего звена:

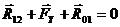
По этому уравнению построим план сил в масштабе.

Величина реакции 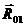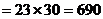Н.