Оценочные средства для входного контроля
УтверждЕН
на заседании кафедры
«___»__________20__ г., протокол №___
Заведующий кафедрой
__________________ А.И Замыслова
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ
по дисциплине
«Линейная алгебра. Аналитическая геометрия.
Начала анализа»
Направление подготовки: 13.03.01 Теплоэнергетика и теплотехника
Профиль подготовки: Тепловые электрические станции
Наименование образовательной программы: Тепловые электрические станции
Квалификация (степень) выпускника:бакалавр
Форма обучения: очная
г. Волгодонск, 2017 г.
Паспорт
Фонда оценочных средств
1.1.Модели контролируемых компетенций:
Оценочные средства для текущего контроля направлены на проверку знаний и умений студентов, являющихся основой формирования у обучающихся следующих компетенций:
ОПК-2 - способностью демонстрировать базовые знания в области естественнонаучных дисциплин, готовностью выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности; применять для их разрешения основные законы естествознания, методы математического анализа и моделирования, теоретического и экспериментального исследования
ОПСК-1 – готовностью применять базовые знания в области математических и естественных наук в профессиональной деятельности
Согласно Рабочему учебному плану направления, в формировании данных компетенций участвуют дисциплины:
ОПК-2 – линейная алгебра, аналитическая геометрия, начала анализа, дифференциальные уравнения, теория рядов, теория вероятностей, математическая статистика, физика, теоретическая механика, прикладная механика, общая физика, электротехника и электроника, материаловедение и технология конструкционных материалов, механика жидкостей и газов, турбомашины, архитектура информационных систем, моделирование систем, основы математического моделирования и численные методы, автоматизация АЭС, учебная и производственная практика;
ОПСК-1 - линейная алгебра, аналитическая геометрия, начала анализа, дифференциальные уравнения, теория рядов, теория вероятностей, математическая статистика, общая физика, основы теории автоматического управления, механика жидкостей и газов, архитектура информационных систем, теория автоматического управления, автоматизация АЭС, учебная практика.
В результате освоения дисциплины студенты, для формирования данных компетенций студенты должны:
1) Знать:
В результате освоения дисциплины для формирования данных компетенций студенты должны:
1) знать:
З1 - определения, теоремы всех разделов высшей математики;
З2 - основные методы аналитической геометрии, линейной алгебры, дифференциального и интегрального исчисления.
2) уметь:
У1 - решать типовые математические задачи;
У2 - самостоятельно использовать математический аппарат, содержащийся в литературе по теплоэнергетике, расширять свои математические познания.
3) Владеть:
В1 - первичными навыками и основными методами решения математических задач из общеинженерных и специальных дисциплин специализации.
1.2. Программа оценивания контролируемой компетенции:
| № п/п | Контролируемые разделы дисциплины | Код контролируемой компетенции (или ее части) | Наименование оценочного средства | ||
| текущий контроль успеваемости (неделя, форма) | аттестация раздела (неделя, форма) | Промежуточная аттестация | |||
| Линейная и векторная алгебра. | ОПК-2, ОПСК-1 | 3КР | 5КР | УО по билетам | |
| Аналитическая геометрия. | ОПК-2, ОПСК-1 | 9КР | 10ИДЗ | УО по билетам | |
| Введение в математический анализ. | ОПК-2, ОПСК-1 | 12КР | 13КР | УО по билетам | |
| Дифференциальное исчисление функций одной переменной. | ОПК-2, ОПСК-1 | 14ИТ | 17КР | УО по билетам |
КР – контрольная работа; ИДЗ – индивидуальное домашнее задание; ИТ – интернет-тестирование; УО - устный опрос.
1.3. Основные показатели оценивания компетенций:
Соотнесение формируемых компетенций со знаниями, умениями и навыками приведено в следующей таблице:
| Индекс компетенции | Проектируемые результаты освоения дисциплины «Математика» и индикаторы формирования компетенций | Средства и технологии оценки | ||
| Знания (З) | Умения (У) | Навыки (В) | ||
| ОПК-2, ОПСК-1 | 3 1, З2 | У1, У2 | В1 | Т, СР, КР, УО по билетам, ИДЗ |
Основные показатели оценивания знаний, умений и навыков, необходимых для формирования компетенций, представлены в таблице:
| Результаты обучения (освоенные умения, усвоенные знания) | Основные показатели оценки результатов | Формируемые компетенции |
| З1 - определения, теоремы всех разделов высшей математики; | Определения матриц, выполнение операций над матрицами. Определения определителей, вычисление определителей, миноров, алгебраических дополнений, обратной матрицы. Определение линейного пространства, линейной зависимости и независимости векторов, размерности пространства. Евклидово пространство, определение скалярного произведения, векторного произведения, смешанного произведения. Уравнение поверхности тел. Определения кривых второго порядка, вывод уравнений кривых второго порядка. Уравнение плоскости по заданным элементам. Уравнение прямой в пространстве и на плоскости по заданным элементам. Определение множества, операций над множествами. Функция, ее свойства. Определение числовой последовательности, сходимость последовательности, свойства последовательностей. Предел последовательности. Теорема Больцано-Вейерштрасса. Существование предела у монотонной последовательности. Ограниченность последовательности, имеющей предел. Предел функции. Единственность предела. Бесконечно малые функции. Теоремы о пределах. Композиция (суперпозиция) функций. Теоремы о предельном переходе в неравенствах. Сравнение бесконечно малых. Обратные функции. Непрерывность функции. Точки разрыва и их классификация. Теоремы о непрерывных функциях. Производная, ее свойства. Производная сложной функции, обратной, заданной параметрически, не явно. Связь между непрерывностью функции и существованием производной. Геометрический, механический смысл производной. Логарифмическое дифференцирование. Определение дифференциала.. | ОПК-2, ОПСК-1 |
| З2 - основные методы аналитической геометрии, линейной алгебры, дифференциального и интегрального исчисления. | Нахождение обратных матриц. Методы решения систем линейных уравнений. Доказательство линейной зависимости и независимости линейных векторов, базиса линейного пространства. Разложение вектора по базисным. Вычисление углов, площадей поверхности и объемов тел. Вычисление углов между векторами, прямыми, прямой и плоскостью, плоскостями. Запись уравнений плоскости и прямой по заданным элементам. Вычисление пределов последовательности и функции. Вычисление производных по определению, производной элементарных функций, по правилам вычисления производных, логарифмическим дифференцированием, производной сложной функции, обратной, заданной неявно, параметрически. Нахождение подмножеств, объединений и пересечений множеств. Построение графиков функций, ее свойства. Вычисление предела последовательности. Вычисление предела функции, в том числе с помощью замечательных пределов, правила Лопиталя. Доказательство непрерывности функции, определение точек разрыва и их классификация. Вычисление производной с помощью определения и таблицы. Находить производную сложной функции, обратной, заданной параметрически, не явно. Записывать уравнение касательной, нормали, находить скорость, ускорение. Применять понятие дифференциала к приближенным вычислениям. | ОПК-2, ОПСК-1 |
| У1 - решать типовые математические задачи | Находить обратные матрицы. Решать системы линейных уравнений. Доказывать линейную зависимость и независимость линейных векторов, находить базис линейного пространства. Раскладывать вектор по базисным. Вычислять углы, площади поверхности и объемы тел. Вычислять углы между векторами, прямыми, прямой и плоскостью, плоскостями. Записывать уравнения плоскости и прямой по заданным элементам. Находить подмножества, объединений и пересечений множеств. Строить графиков функций. Вычислять пределы последовательности и функции, в том числе с помощью замечательных пределов, правила Лопиталя. Вычислять производные по определению, производные элементарных функций, по правилам вычисления производных, логарифмическому дифференцированию, производную сложной функции, обратной, заданной неявно, параметрически. Доказательство непрерывности функции, определение точек разрыва и их классификация. Записывать уравнение касательной, нормали, находить скорость, ускорение. Применять понятие дифференциала к приближенным вычислениям. | ОПК-2, ОПСК-1 |
| У2 - самостоятельно использовать математический аппарат, содержащийся в литературе по теплоэнергетике, расширять свои математические познания. | Уметь решать математические задачи из числа общеинженерных и специальных дисциплин | ОПК-2, ОПСК-1 |
| В1 - первичными навыками и основными методами решения математических задач из общеинженерных и специальных дисциплин специализации. | Владеть методами решения всех выше перечисленных типовых задач при решении математических задач из общеинженерных и специальных дисциплин | ОПК-2, ОПСК-1 |
ТИПОВЫЕ КОНТРОЛЬНЫЕ ЗАДАНИЯ
для оценки знаний, умений, навыков по дисциплине
Типовые контрольные задания представлены в соответствии с перечнем оценочных средств по дисциплине в следующей структуре:
- методические материалы, определяющие процедуры оценивания знаний, умений, навыков, характеризующих этапы формирования компетенций;
- сами оценочные средства ;
- критерии и шкалы оценивания.
Вариант 1
1) Даны матрицы 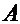 и
и 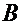 , числа
, числа 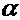 и
и 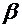 .
.
Вычислить: а) 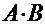 ; б)
; б) 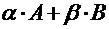 ; в)
; в) 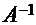 .
.
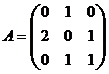
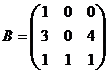
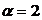 ;
; 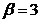
Решение:
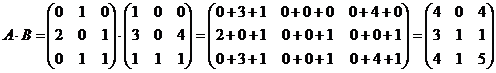
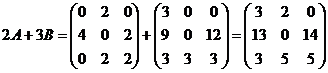
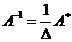
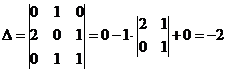
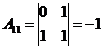
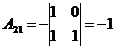
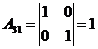
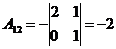
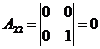
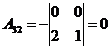
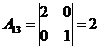
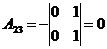
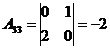
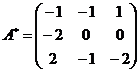
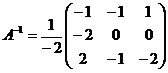
2) Решить систему линейных уравнений по формулам Крамера
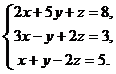
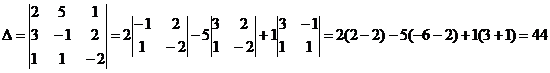
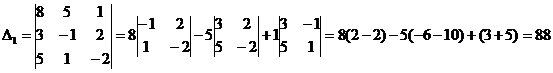
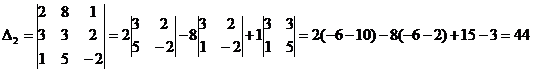
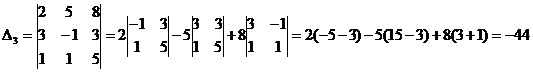
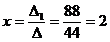
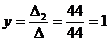
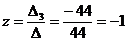
Ответ: 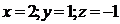
3) Найти С из уравнения: 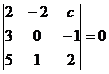
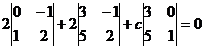 ; 2(0+1)+2(6+5)+c(3-0)=0; 3c=-24; c=-8.
; 2(0+1)+2(6+5)+c(3-0)=0; 3c=-24; c=-8.
Вариант 2
1) Даны матрицы 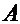 и
и 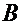 , числа
, числа 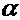 и
и 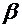 .
.
Вычислить: а) 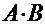 ; б)
; б) 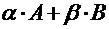 ; в)
; в) 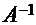 .
.
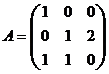
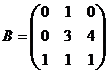
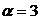
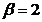
Решение:
1) 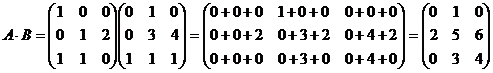
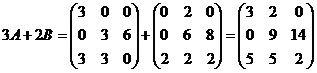
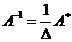
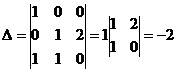
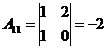
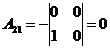
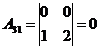
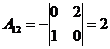
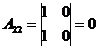
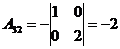
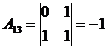
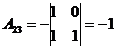
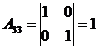
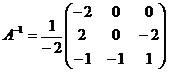
2) Решить систему методом Крамера: 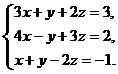
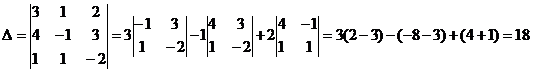
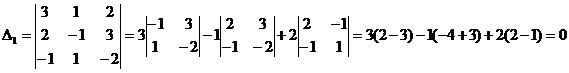
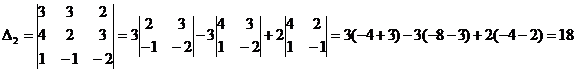
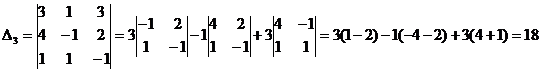
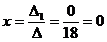
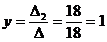
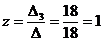
Ответ: 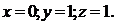
3) Найти с из уравнения: 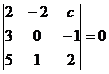
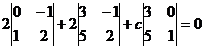 ;
; 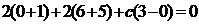 ;
; 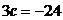 ;
; 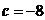
Критерии оценки контрольной работы(30 мин.)
| Правильно решенное 1 задание и вычислительные ошибки в остальных | |
| Правильно решенные 2 задания и вычислительная ошибка в третьем | |
| Правильно решенные 3 задания |
Тестовые задания по разделу «Линейная и векторная алгебра»(5Т,5б)
1. Вычислить определитель второго порядка 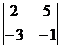 . Варианты ответов: 1) . Варианты ответов: 1) 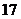 2) 2) 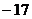 3) 13 4) 3) 13 4) 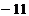 |
2. Найти значение 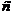 из уравнения: из уравнения: 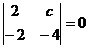 . Варианты ответов: 1) . Варианты ответов: 1) 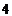 2) 2) 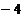 3) 3) 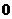 4) 4) 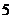 . . |
3. Вычислить определитель третьего порядка 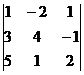 . Варианты ответов: 1) . Варианты ответов: 1) 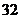 2) 2) 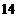 3) 3) 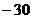 4) 4) 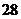 . . |
4. Найти с из уравнения: 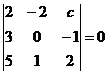 . Варианты ответов: 1) . Варианты ответов: 1) 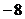 2) 2) 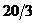 3) 3) 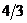 4) 4) 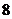 |
5. Найти произведение матриц 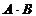 , если , если 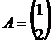 , , 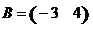 . Варианты ответов: 1) . Варианты ответов: 1) 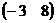 ; 2) ; 2) 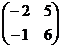 ; 3) ; 3) 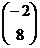 4) 4) 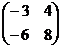 . . |
6. Найти произведение матриц 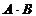 , если , если 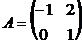 , , 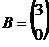 . Варианты ответов: 1) . Варианты ответов: 1)  2) 2) 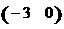 3) 3) 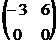 4) 4)  |
7. Найти матрицу 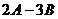 , если , если 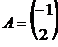 , , 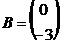 . Варианты ответов: 1) . Варианты ответов: 1)  2) 2)  3) 3) 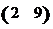 4) 4)  . . |
8. Найти обратную матрицу 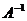 к матрице к матрице 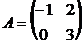 . Варианты ответов: 1) . Варианты ответов: 1) 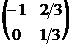 2) 2) 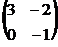 3) 3) 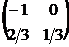 4) 4) 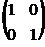 |
9. Найти обратную матрицу 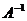 к матрице к матрице 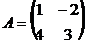 . Варианты ответов: 1) . Варианты ответов: 1) 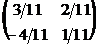 ; 2) ; 2) 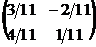 ; 3) ; 3) 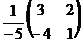 ; 4) ; 4) 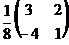 |
10. Найти обратную матрицу 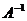 к матрице к матрице 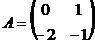 . Варианты ответов: 1) . Варианты ответов: 1) 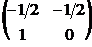 2) 2) 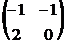 3) 3) 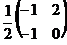 4) 4) 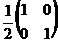 |
11. Даны две точки 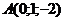 и и 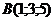 . Найти длину вектора . Найти длину вектора  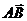 . Варианты ответов: 1) . Варианты ответов: 1) 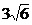 , 2) , 2) 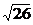 , 3) , 3) 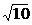 , 4) , 4) 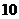 . . |
12. Найти сумму направляющих косинусов вектора 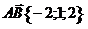 . Варианты ответов: 1) . Варианты ответов: 1) 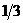 2) 2) 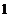 3) 3) 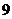 4) 4) 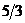 . . |
13. Векторы 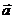 и и 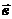 образуют угол образуют угол 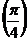 . Зная, что . Зная, что 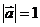 , , 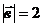 , вычислить , вычислить 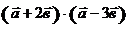 . Варианты ответов: 1) . Варианты ответов: 1) 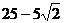 ; 2) ; 2) 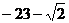 ; 3) ; 3) 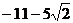 4) 4) 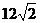 . . |
14. Векторы 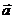 и и 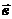 образуют угол образуют угол  . Зная, что . Зная, что 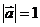 , , 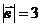 , вычислить , вычислить 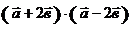 . Варианты ответов: 1) . Варианты ответов: 1) 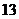 2) 2) 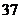 3) 3) 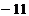 4) 4) 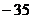 |
15. Найти разность проекций вектора 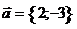 на координатные оси на координатные оси 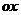 и и 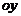 соответственно. Варианты ответов: 1) соответственно. Варианты ответов: 1) 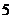 2) 2) 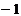 3) 3) 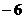 4) 4)  . . |
16. Найти проекцию вектора 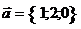 на вектор на вектор 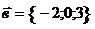 . Варианты ответов: 1) . Варианты ответов: 1) 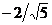 2) 2) 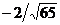 3) 3) 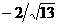 4) 4) 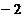 |
17. Найти скалярное произведение векторов 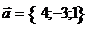 и и 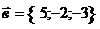 . Варианты ответов: 1) . Варианты ответов: 1) 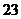 2) 2) 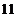 3) 3) 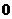 4) 4) 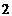 . . |
18. Найти скалярное произведение векторов 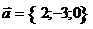 и и 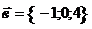 . Варианты ответов: 1) . Варианты ответов: 1) 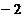 , 2) , 2) 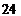 , 3) , 3) 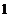 , 4) , 4) 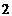 . . |
19. Заданы точки 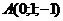 , , 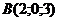 , , 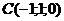 . Скалярное произведение векторов . Скалярное произведение векторов 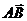 и и 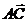 равно Варианты ответов: 1) равно Варианты ответов: 1) 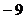 2) 2) 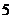 3) 3) 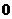 4) 4) 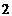 . . |
20. Заданы точки 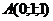 , , 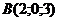 , , 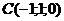 . Найти угол между векторами . Найти угол между векторами 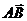 и и 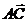 . Варианты ответов: 1) . Варианты ответов: 1) 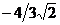 2) 2) 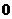 3) 3) 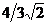 4) 4) 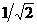 . . |
21. Найти внутренний угол 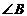 треугольника с вершинами в точках треугольника с вершинами в точках 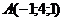 , , 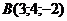 , , 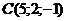 . Варианты ответов: 1) . Варианты ответов: 1) 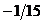 2) 2) 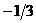 3) 3) 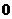 4) 4)  . . |
22. Найти координату 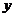 , при которой векторы , при которой векторы 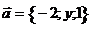 и и 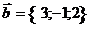 перпендикулярны. Варианты ответов: 1) перпендикулярны. Варианты ответов: 1) 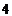 , 2) , 2) 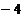 , 3) , 3) 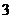 , 4) , 4) 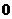 . . |
23. Найти координату 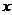 , при которой векторы , при которой векторы 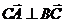 , если , если 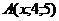 , , 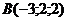 , , 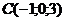 . Варианты ответов: 1) . Варианты ответов: 1) 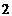 2) 2) 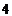 3) 3) 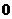 4) 4) 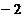 . . |
24. Найти 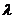 , при котором векторы , при котором векторы 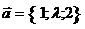 и и 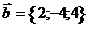 коллинеарны. Варианты ответов: 1) коллинеарны. Варианты ответов: 1) 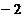 2) 2) 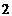 3) 3) 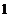 4) 4) 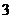 . . |
25. Найти 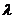 , при котором векторы , при котором векторы 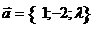 и и 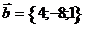 коллинеарны. Варианты ответов: 1) коллинеарны. Варианты ответов: 1) 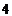 2) 2) 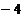 3) 3) 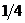 4) 4) 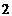 . . |
26. Найти площадь параллелограмма, построенного на векторах 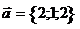 и и 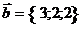 . Варианты ответов: 1) . Варианты ответов: 1) 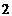 2) 2) 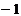 3) 3) 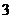 4) 4)  . . |
27. Найти площадь треугольника с вершинами в точках 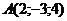 , , 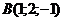 , , 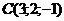 . Варианты ответов: 1) . Варианты ответов: 1) 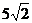 2) 2) 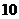 3) 3) 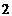 4) 4) 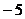 . . |
28. Найти объем пирамиды с вершинами в точках 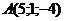 , , 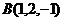 , , 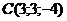 , , 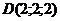 . Варианты ответов: 1) . Варианты ответов: 1) 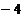 2) 2) 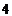 3) 3) 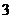 4) 4) 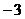 . . |
29. При каком значении 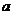 векторы, соединяющие точки векторы, соединяющие точки 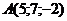 , , 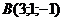 , , 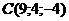 , , 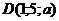 , компланарны. Варианты ответов: 1) , компланарны. Варианты ответов: 1) 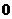 2) 2) 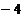 3) 3) 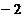 4) 4) 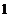 . . |
30. При каком 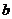 четыре точки четыре точки 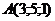 , , 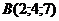 , , 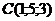 , , 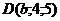 лежат в одной плоскости. Варианты ответов: 1) лежат в одной плоскости. Варианты ответов: 1) 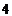 2) 2) 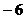 3) 3) 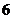 4) 4) 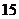 . . |
Ключ к ответу:
Время выполнения: 80 мин
Критерии оценивания: 28-30 заданий -10 баллов
25-27заданий – 9 баллов
22-24 заданий – 8 баллов
18-21 заданий -7 баллов
15-17 заданий – 6 баллов
Результат поделить на 2, т.к. тест оценивается 5баллами.
Вариант 1
1.Даны координаты вершины пирамиды 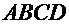 :
: 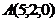 ,
, 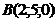 ,
, 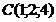 ,
, 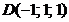
Найдем а) угол  между векторами
между векторами 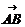 и
и 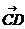 :
:
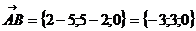 ;
; 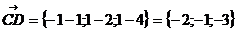
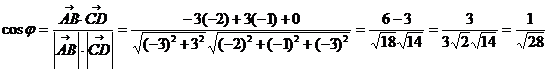

б) площадь треугольника АВС: 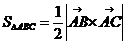
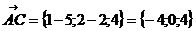
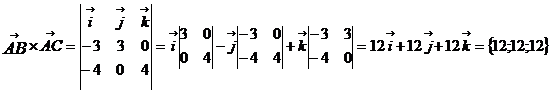
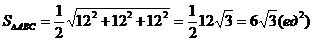
в) объем пирамиды ABCD
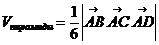
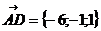
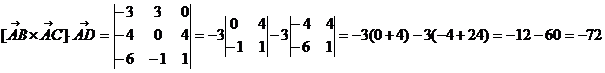
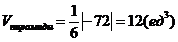
г) высоту 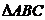 ,опущенную из вершины С:
,опущенную из вершины С: 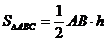
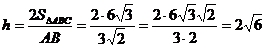
д) высоту пирамиды 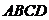 , опущенную из вершины D:
, опущенную из вершины D: 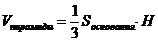
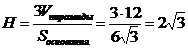
2. Даны 3 точки 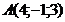
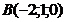
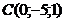
Написать:
1)канонические и параметрические уравнения прямой АВ
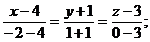 канонические уравнения прямой:
канонические уравнения прямой: 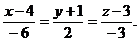
Параметрические уравнения прямой АВ: 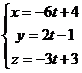
2) Написать уравнение плоскости, проходящей через точку А перпендикулярно вектору 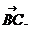
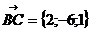 - вектор нормали к искомой плоскости, на которой лежит точка А(4;-1;3). Уравнение плоскости имеет вид:
- вектор нормали к искомой плоскости, на которой лежит точка А(4;-1;3). Уравнение плоскости имеет вид:  2(x-4)-6(y+1)+1(z-3)=0; 2x-6y+z-17=0
2(x-4)-6(y+1)+1(z-3)=0; 2x-6y+z-17=0
3) уравнение плоскости АВС.
Пусть точка М(x;y;z)- текущая точка плоскости.
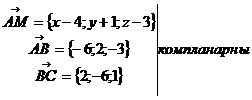
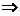 Условие компланарности
Условие компланарности 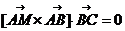
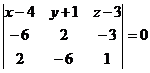
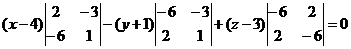
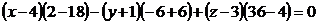
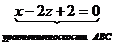
4) Найти угол 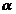 между прямой L:
между прямой L: 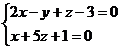 и плоскостью АВС.
и плоскостью АВС.
Вектор нормали к плоскости АВС 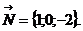 Найдем направляющий вектор
Найдем направляющий вектор 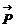 прямой L :
прямой L :
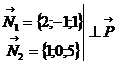

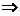
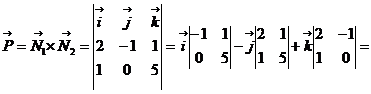
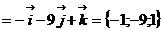
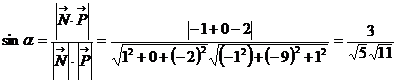
 .
.
5) Написать уравнение плоскости, проходящей через точку 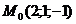 и прямую
и прямую 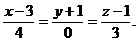
Решение: Из уравнения прямой следует, что точка 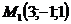 , направляющий вектор прямой
, направляющий вектор прямой 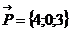 лежат в искомой плоскости. Пусть точка
лежат в искомой плоскости. Пусть точка 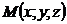 текущая точка плоскости, тогда
текущая точка плоскости, тогда
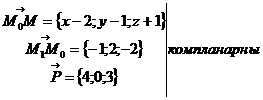
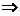
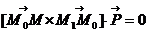
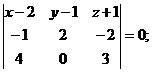
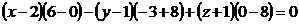
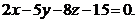
Вариант 2
1. Даны координаты вершины пирамиды 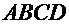 :
: 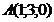 ,
, 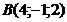 ,
, 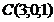 ,
, 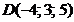
Найдем:
а) угол  между векторами
между векторами 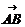 и
и 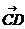 :
:
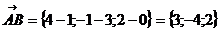 ;
; 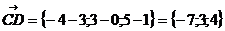
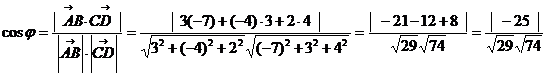
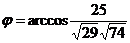
б) площадь треугольника АВС: 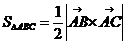
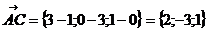
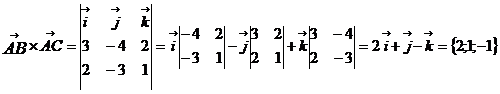
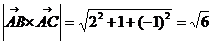
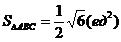
в) объем пирамиды ABCD
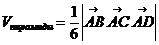
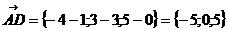
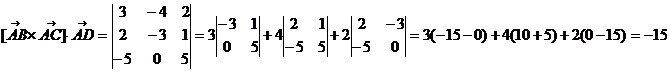
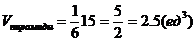
г) высоту 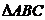 ,опущенную из вершины С:
,опущенную из вершины С: 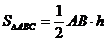
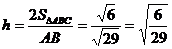
д) высоту пирамиды 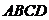 , опущенную из вершины D:
, опущенную из вершины D: 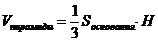
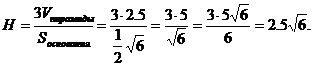
2. Даны 3 точки 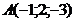 ,
, 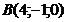 ,
, 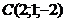
Написать:
1)канонические и параметрические уравнения прямой АВ.
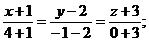 канонические уравнения прямой:
канонические уравнения прямой: 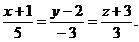
Параметрические уравнения прямой АВ: 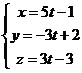
2) Написать уравнение плоскости, проходящей через точку А перпендикулярно вектору 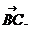
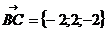 - вектор нормали к искомой плоскости, на которой лежит точка А(4;-1;3). Уравнение плоскости имеет вид: -2(x+1)+2(y-2)-2(z+3)=0; x-y+z+6=0.
- вектор нормали к искомой плоскости, на которой лежит точка А(4;-1;3). Уравнение плоскости имеет вид: -2(x+1)+2(y-2)-2(z+3)=0; x-y+z+6=0.
3) уравнение плоскости АВС.
Пусть точка М(x;y;z)- текущая точка плоскости.
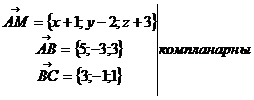
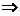 Условие компланарности
Условие компланарности
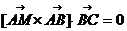
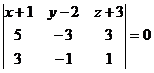
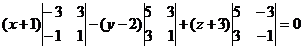
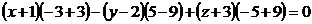
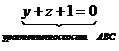
4) Найти угол 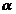 между прямой L:
между прямой L: 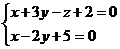 и плоскостью АВС.
и плоскостью АВС.
Вектор нормали к плоскости АВС 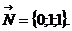 Найдем направляющий вектор
Найдем направляющий вектор 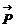 прямой L :
прямой L :
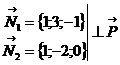

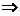
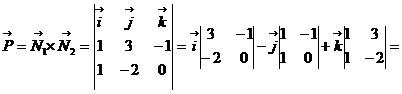
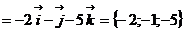
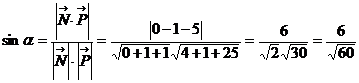
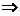

5) Написать уравнение плоскости 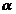 , проходящей через 2 параллельные прямые
, проходящей через 2 параллельные прямые
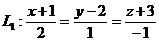 и
и 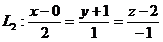
Пусть точка
