Соотношения между напряжениями и деформациями и потенциальная энергия линейного упругого тела.

У линейного упругого тела компоненты тензоров напряжений и деформаций связаны линейными зависимостями.

(e) = (а)(s), (19)

или (s) = (с)(e), (20)

где

(e)=(e_x,e_y,e_z,g_xy,g_yz,g_zx)^T - матрица-столбец, составленная из компонент тензора деформаций,

(s) = (s_x,s_y,s_z,t_xy,t_yz,t_zx)^Т - матрица-столбец, составленная из компонент тензора напряжений,

(а) – матрица (6х6) упругих коэффициентов податливости материала,

(с) = (а)^-1 _{_}-_{_} матрица упругих коэффициентов жесткости материала.

В п.10 показано, что компоненты тензоров деформаций и напряжений могут быть интерпретированы как обобщенные перемещения и соответствующие им обобщенные силы. Поэтому матрицам (а) и (с) присущи все свойства, описанные в п.п. 7 и 8 для матриц жесткости и податливости линейных упругих систем.

Следовательно, обе матрицы симметричны относительно главной диагонали. Поэтому из 36 коэффициентов каждой из них 21 коэффициент может быть независимым. В общем случае линейно упругого материала его упругие свойства описываются 21-й упругой постоянной.

Потенциальная энергия единицы объема линейного упругого тела п может быть представлена в виде однородной квадратичной функции компонент тензора напряжений, коэффициентами которой являются компоненты матрицы податливости:

п (s) = 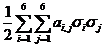(21)

или однородной квадратичной функцией компонент тензора деформаций, коэффициентами которой являются компоненты матрицы жесткости:

п (e) = 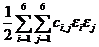(22)

И, наконец, формула (13) в обозначениях этого параграфа принимает вид:

п (s,e) = 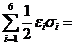1/2(s_xe_x + s_ye_y + ... + t_zxg_zx) =1/2 (s· ·e),(23)

следовательно,

потенциальная энергия единицы объема линейного упругого тела равна половине свертки тензора напряжений с тензором деформаций.

Если известны функции (21) или (22), то уравнения, связывающие напряжения и деформации могут быть получены по формулам теорем Лагранжа (15) и Кастильяно (16):

s_j = 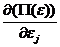(24)

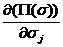e_j = (25)

Разумеется, что те же результаты получатся, если коэффициенты квадратичных форм (21) и (22) подставить в соотношения (19) и (20).

Преобразуем выражение (23), представив тензоры напряжений и деформаций суммой шаровых тензоров и девиаторов:

s =s₀I + D_s ,s₀ = ,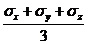

e =1/3 qI + D_e ,q = e_x+e_y+e_z

где I – единичный тензор, s₀ –среднее нормальное напряжение, q - относительное изменение объема. Получим

п = 1/2(s₀I + D_s)· ·(1/3 qI + D_e)=

=1/6 s₀q(I· · I)+1/2s₀(I· · D_e) +1/6q(D_s· · I) +1/2(D_s· · D_e )(26).

ВсНапомним, что девиатор – это такой тензор, у которого равен нулю первый инвариант, то есть сумма элементов, стоящих на главной диагонали. Легко проверяется, что свертка девиатора с единичным тензором равна нулю, поэтому в ноль обращаются второе и третье слагаемые в (26). Свертка двух единичных тензоров равна 3, поэтому первое слагаемое превращается в 1/2s₀q.

В результате, формула (26) принимает вид:

п = 1/2s₀q + 1/2(D_s· · D_e ) = п_ио + п_иф.(27)

Первое слагаемое называют энергией изменения объема:

п_ио =1/2s₀q (28),

а второе – энергией изменения формы:

п_иф =1/2(D_s· · D_e )(29).