Статически неопределимые стержневые системы. Степень статической неопределимости. Лишние связи. Выбор основной системы, составление канонических уравнений, их физический смысл.

Степень статической неопределимости системы

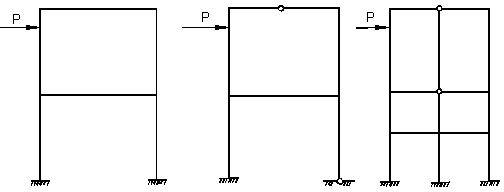
Перед расчетом статически неопределимой конструкции необходимо сначала определить степень статической неопределимостирассматриваемойсистемы. Для балок и простых рам степень статической неопределимости равна числу лишних опорных связей. В каждой связи возникает опорная реакция, поэтому степень статической неопределимости можно найти, сосчитав разность между количеством неизвестных опорных реакций и числом независимых уравнений статики.

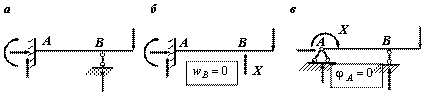
Рис.1

Например, балка на рис. 1, а является один раз статически неопределимой, так как имеет 4 связи и 4 неизвестные опорные реакции, а количество независимых уравнений равновесия – 3. В раме, показанной на рис. 3, а, число наложенных связей и опорных реакций в них равно 5, и эта рама является дважды статически неопределимой. Если в один из стержней балки (рамы) врезан шарнир, то количество связей уменьшается на единицу, так как становится возможным взаимный поворот сечений, примыкающих к шарниру. Появляется дополнительное уравнение для определения опорных реакций: "изгибающий момент в шарнире равен нулю" или можно сказать по-другому: "сумма моментов всех сил, расположенных слева (или справа) от шарнира, равна нулю". Так, балка с врезанным в точке Е шарниром, показанная на рис. 2, а, является один раз статически неопределимой: от 5 опорных связей надо вычесть одну связь, связанную с наличием дополнительного шарнира в точке Е. Из четырех оставшихся связей одна является лишней. Можно сосчитать степень статической неопределимости этой балки и иначе: для определения пяти опорных реакций можно составить четыре уравнения статики (дополнительное уравнение "изгибающий момент в шарнире Е равен нулю"). Разность между числом реакций и количеством уравнений статики равна единице, то есть балка один раз статически неопределима.

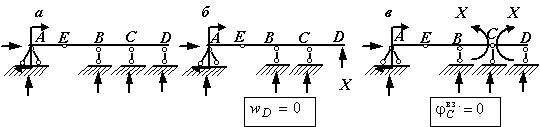
Рис.2

Рис.3

Следует различать внешне статически неопределимые и внутренне статически неопределимые системы.

Внешне статически неопределимой называют такую систему, которая имеет только лишние внешние связи, т.е. лишние опорные за­крепления. Примером внешне статически неопределимой плоской системы являетсятрехпролетная рама (рис. 4).

Рис.4

Степень статической неопределимости внешне статически неопределимой системы S легко установить путем вычитания из общего числа опорных стержней m количество независимых урав­нений равновесия n, которое может быть составлено для данной системы (одно - для одномерных; три - для плоских и шесть - для пространственных систем).

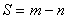. (14.1)

Для плоской рамы, изображенной на рис.4, учитывая, что защемление эквивалентно трем опорным стержням, получаем:

m = 3 + 2×2 +1 = 8; S = m - n = 8-3 = 5,

т.е. данная система 5 раз статически неопределима.

Внутренне статически неопределимой называют сис­тему, обладающую лишними связями, введенными для взаимного соединения частей системы.

Двухопорная рама с затяжкой (рис. 5, а) внутренне один раз статически неопределима. Статически определимая система (рис. 5, б) получена из заданной (рис. 5, а) путем разрезания за­тяжки ab. И при этом взаимодействие частей затяжки заменяется только одной неизвестной осевой силой N₁. Следовательно, в ста­тически определимой системе, изображенной на рис. 5, б имеем одно лишнее неизвестное N₁ , которое невозможно определить при помощи метода сечений. Поэтому заданная система (рис. 5, а) яв­ляется один раз статически неопределимой.

Если затяжку жестко заделать в стойки, как это показано на рис. 6, а, то получим трижды статически неопределимую систему.

Действительно, в данном случае после разрезания нижнего ригеля ab, взаимодействие частей ac и bc характеризуется уже тремя неизвестными усилиями N₁, Q₁, M₁(рис.6, б), которые нельзя определить из условия равновесия. Поэтому система, изображенная на рис. 6, a является три раза внутренне статически неопредели­мой.

Рис.5 Рис.6

Отсюда можно сделать вывод, что в плоских системах, замк­нутый бесшарнирный контур имеет три лишние связи. Следова­тельно, если плоская система содержит n замкнутых контуров, то она, очевидно, будет 3n раз статически неопределима.

На рис. 7 показана плоская рама, имеющая в первом (а) случае три внешние связи, а во втором случае (б) - пять. Значит, в первом случае рама имеет необходимое для статической определи­мости количество внешних связей, а во втором же - две дополни­тельные внешние связи. Однако в обеих ситуациях рама статически неопределима, т.к. конфигурация ее такова, что не позволяет опре­делить усилия во всех ее элементах, используя только уравнения равновесия. Следовательно, для окончательного ответа на вопрос о статической определимости системы необходимо проведение сов­местного анализа наложенных на систему внешних и внутренних связей.

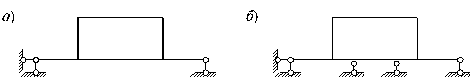
Рис. 7

Рассмотрим другие рамы, которые содержат замкнутые контуры (рис.8).

а) б) в)

Рис.8

Первая рама (рис.8,а) имеет шесть простых внешних связей при трёх необходимых для плоской системы. Следовательно, система имеет Л = 6 – 3 = 3 лишние внешние связи. Система имеет один замкнутый контур К= 1, который имеет три лишние внутренние простые связи, т.е. трижды статически неопределим. Следовательно, степень статической неопределимости системы 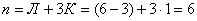. Вторая рама (рис.8, б) имеет пять внешних простых связей при трёх необходимых. Следовательно, Л=5–3=2 и система внешним образом дважды статически неопределима. Система имеет два замкнутых контура К=2, каждый из которых трижды статически неопределим, следовательно, внутренним образом система 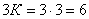шесть раз была бы статически неопределима, если бы не было внутреннего шарнира. Последний соединяет три стержня (m = 3) и поэтому даёт системе (m – 1) = 3–1=2 степени свободы. Таким образом, степень свободы статической неопределимости второй рамы можно вычислить по общей формуле:

,

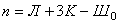где Ш₀ – число простых врезанных шарниров, К – число замкнутых контуров, Л – число лишних внешних связей.

В результате получаем: .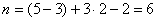

Третья рама (рис.8, в) имеет Л = 9 – 3 = 6, К = 4, Ш₀ = 2 + 3 = 5, следовательно, .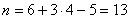

Отметим, что степень статической неопределимости стержневой системы и её степень свободы связаны равенством .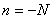

Рассмотрим еще несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 9 показано несколько рам. Последовательно рассмотрим их.

а) Рама имеет четыре дополнительные внешние связи и три взаимные связи, т. е. семь раз статически неопределима.

б) Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.

Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира. Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти — три раза статически неопределимой.

Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня и шарнир снимает две связи.

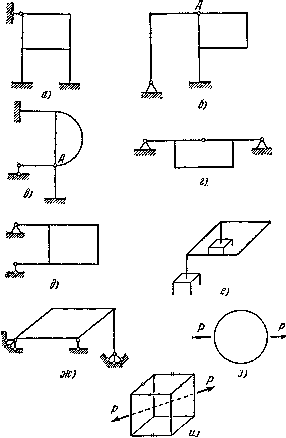
Рис.9. Примеры рамных статически неопределимых конструкций:

а) статически неопределимая — семь, б) — три, в) — четыре, г) — три,

е) — двенадцать, ж) — семь, и) — тридцать раз статически неопределима

в) Если бы шарнир А отсутствовал, система была бы четыре раза внешним образом и три раза внутренним образом статически неопределимой, т.е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т. е. три связи. Рама четыре раза статически неопределима.

г) Рама три раза статически неопределима.

д) Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это — механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.

е) Рама — пространственная. Имеется шесть дополнительных внешних связей (лишняя заделка) и шесть дополнительных взаимных связей (замкнутый контур). Система 12 раз статически неопределима.

ж) Система семь раз статически неопределима (один раз внешним образом и шесть раз — внутренним).

з) Здесь для плоской рамы не показаны внешние связи, но дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае условились считать, что дополнительных внешних связей нет, и положение рамы в пространстве считается определенным; рассматриваются только внутренние связи. Система три раза статически неопределима.

и) Здесь также рассматриваются только внутренние связи, поскольку система указанных внешних сил удовлетворяет условиям равновесия. Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного замкнутого контура. Таких сечений следует сделать пять (см. рис. 9, и). Система 30 раз статически неопределима.

Метод сил

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил».