Билет1 (ФНП:предел и непрерывность)
Билет1 (ФНП:предел и непрерывность)
U=f(x,y) 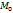 (
( 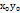 ) δ-окр
) δ-окр
Зафиксируем у и придадим х приащение ∆х х- 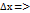 U-приращение
U-приращение
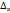 U=f(
U=f( 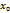 +
+ 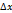 ,
, 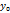 )- f(
)- f( 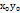 )
)
x-фикс, у-∆у=>∆yU=f( 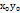 +∆y)- f(
+∆y)- f( 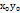 )
)
если же х и у получат приращение, тогда мы получим полное приращение
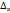 U=f(
U=f( 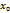 +
+ 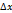 ,
, 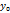 +∆у)- f(
+∆у)- f( 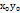 )
)
Опр:Число А наз-ся пределом ф-и U(x;y) в (.) 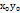 при стремлении точки х,у в (.) х0,у0 прооизвольным образом, если для всех Е>0 существует ∆>0:
при стремлении точки х,у в (.) х0,у0 прооизвольным образом, если для всех Е>0 существует ∆>0: 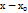 <∆ => f(x,y)=f(
<∆ => f(x,y)=f( 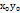 )<E
)<E
Опр:ф-я U=f(x,y) называется непрерывной в точке 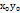 , если она определена в этой точке, и ее окрестности и
, если она определена в этой точке, и ее окрестности и  = f(
= f( 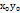 )
)
Опр:ф-я U непрерывна на множество Д, если она непрерывна в каждой точке этого множества
Св-ва непрерывной ф-и одного переменного без изменений переносится в данном случае
Билет2(ЧП фнп 1-го и высших порядков)
Опр:производная f( 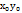 ) ф-и по переменной х в точке
) ф-и по переменной х в точке 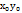 наз-ся ЧП по х от ф-и f(x,y) в точке
наз-ся ЧП по х от ф-и f(x,y) в точке 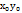
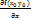 =
= 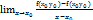
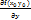 =
= 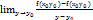
Опр:ЧП от прозводных 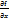 ,
, 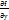 наз-сячп второго порядка
наз-сячп второго порядка
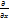 (
( 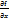 )=
)= 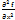
 (
( 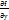 )=
)= 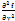
Смешанные ЧП: Теорема:если ф-я z=f(x,y) 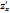 и
и 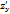 определены и непрерывны, то
определены и непрерывны, то 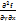 =
= 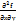 , т.е результат дифференцирования не зависит от пордка дифференцирования
, т.е результат дифференцирования не зависит от пордка дифференцирования
ЧП порядка n это ЧП от порядка (n-1)
Билет3 (дифференциал фнп 1-го и высших порядков)
Опр:ф-я z=f(x,y) в точке наз-ся дифференцируемой в М(х,у), если ее приращение в данной точке можно представить в виде ∆z=A∆x+B∆y+ 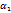 (∆x,∆y)∆x+
(∆x,∆y)∆x+ 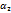 (∆x,∆y)∆y, где АиВ то числа независящие от ∆x,∆y соответственно
(∆x,∆y)∆y, где АиВ то числа независящие от ∆x,∆y соответственно 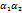 -это БМВ
-это БМВ
Дифференциалом ф-ии I-го порядка наз-ся гл.линейная часть е приращения. Это выражение так же наз-ся полным дифференциалом ф-ии z.
∆z=A∆x+B∆y-полный дифференциал
Т:если ф-я z=f(x,y) дифференциуема в точке (х,у), то z имеет ЧП и А= 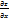 (x,y)
(x,y)
B= 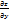 (x,y)
(x,y)
dz= 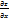 dx+
dx+ 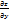 dy
dy
Т2:если ф-я z дифференцируема в точке (х,у), то она непрерывна в данной точке
Опр:полным дифференциалом 2-го порядка ф-и z наз-ся дифференциал ее дифференциала 1-го порядка т.е 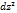 =d(dz)
=d(dz)
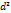 z=
z= 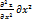 +2
+2 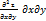 +
+ 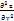 ∂
∂ 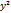
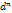 z=
z= 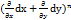 (z)
(z)
Билет4(дифференцирование сложных фнп(с док-вом), дифференциал сложной фнп)
Теорема:Если ф-ии x(t), y(t) – диф-мы в точке t, а ф-я U – диф-ма вв точке (х,у), то ф-я U=(x(t);у(t)) диф-ма в точке t и 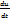 =
= 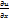 *
* 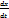 +
+ 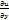 *
* 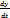 =
= 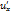 *
* 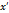 +
+ 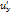 *
* 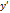
Док-во:
Пусть z=z(x,y), где x=x(u,v), y=y(u,v)
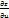 =
= 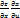 +
+ 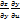
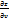 =
= 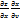 +
+ 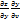
Правило: производная от сложной ф-ии по каждой независимой переменной, есть сумма произведений. ЧП по всем ее промежуточным переменным на производные последних по независимой переменной
Теорема(инвариантность формы полного дифференциала сложной фнп)
Пусть ф-я z=z(u,v), где u=u(x,y) v=v(x,y) => dz= 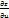 du+
du+ 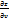 dv
dv
Док-во т.к z=z(u(x,y);v(x,y))=z(x,y) тогда dz= dz= 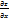 dx+
dx+ 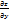 dy
dy
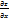 =
= 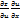 +
+ 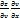
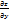 =
= 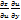 +
+ 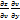
dz= 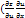 +
+ 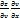 )dx+(
)dx+( 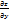 =
= 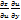 +
+ 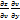 )dy=
)dy= 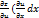 +
+ 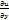 dy)+
dy)+ 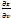 (
( 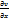 dx+
dx+ 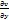 dy)=
dy)= 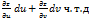
Билет5 (производная неявной фнп)
Теорема если ур-ие F( 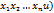 обращается в тождество в точке (
обращается в тождество в точке ( 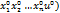 и если в некоторой окрестности этой точки ф-я F непрерывна и имеет непрерывные ЧП при этом
и если в некоторой окрестности этой точки ф-я F непрерывна и имеет непрерывные ЧП при этом 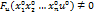 то данное ур-ие имеет в окрестности этой точки единственное решение u=f(
то данное ур-ие имеет в окрестности этой точки единственное решение u=f( 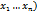 . При этом ф-я F(
. При этом ф-я F( 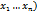 непрерывна и имеет непрерывные ЧП
непрерывна и имеет непрерывные ЧП
Док-во: пусть условие этой теоремы выполнены =) подставляя вместо переменной U ф-ию f получаем тождество F( 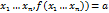 =)полный дифференциал ф-ии F будет равен 0. dF(
=)полный дифференциал ф-ии F будет равен 0. dF( 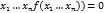 т.е
т.е 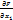 dx+
dx+ 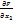 d
d 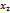 +…+
+…+ 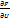 du=0 =) dU=(
du=0 =) dU=( 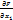 /(-
/(- 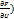 )dx+(
)dx+( 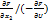 )d
)d 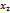 +…+(
+…+( 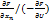 )d
)d 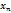
dz= 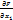 d
d 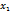 +
+ 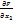 d
d 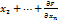 d
d 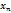
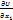 =-
=- 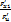 …
… 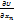 =
= 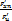
1)F(x,y)=0; т.е y=y(x) 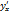 =-
=- 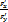
2)F(x,y.z)=0 т.е z=z(x,y,z) 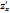 =-
=- 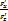
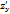 =-
=- 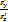
Билет7(двойные интегралы:опр, их св-ва и вычисления)
Свойства двойных интегралов
1. Линейное свойство
 .
.
2. Если функции f (x, y) и g(x, y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и

3. Аддитивное свойство по области интегрирования
 .
.
4. Теорема о среднем. Если функция f (x, y) непрерывна в области D, то в этой области найдется такая точка ( ξ; μ), что
 ,
,
где s — площадь фигуры D.
В двойных интегралах.


Ф-ии х; у однозначные и непрерывные на S.
Пусть  x=x(u;v) y=y(u;v)
x=x(u;v) y=y(u;v)
При замене «х» и «у» на «u» и «v» область S переходит в S’, тогда

Где 

Для двойных интегралов часто используется переход от декартовых к полярным координатам

 тогда
тогда 
 Переход от декартовых координат к полярным целесообразен, если область интегрирования-часть круга.
Переход от декартовых координат к полярным целесообразен, если область интегрирования-часть круга.


В тройных интегралах

Пусть  x=x(u;v;w) y=y(u;v;w) z=z(u;v;w) -однозначны и непрерывны, вместе с ЧП на области S
x=x(u;v;w) y=y(u;v;w) z=z(u;v;w) -однозначны и непрерывны, вместе с ЧП на области S


Наиболее распр. заменами в тройном интеграле являются:
1) Переход к цилиндрическим координатам:

Переход к цилиндрическим координатам целесообразен, если область интегрирования-часть циллинра, или сечения плоскостями, параллельными одной из координатных плоскостей есть часть круга, или круг

2) Переход к сферическим координатам




Свойства рядов Тейлора.
1. Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
2. Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
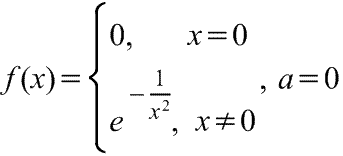
Ряды Тейлора применяются при аппроксимации ( приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=0:
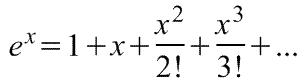
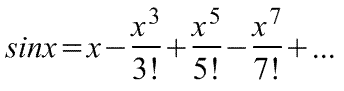
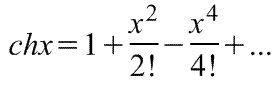
При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:
1) 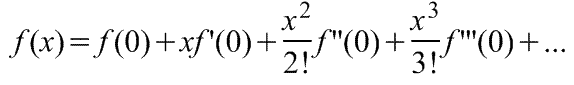 , где f(x) - функция, имеющая при а=0 производные всех порядков. Rn - остаточный член в ряде Маклорена (=Макларена) (Тейлора при а=0)определяется выражением
, где f(x) - функция, имеющая при а=0 производные всех порядков. Rn - остаточный член в ряде Маклорена (=Макларена) (Тейлора при а=0)определяется выражением 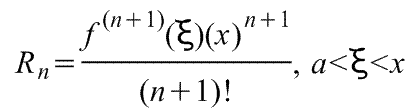
2) 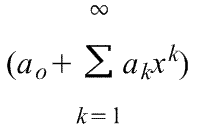
k-тый коэффициент (при хk) ряда определяется формулой
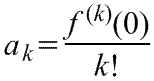
Билет1 (ФНП:предел и непрерывность)
U=f(x,y)  (
(  ) δ-окр
) δ-окр
Зафиксируем у и придадим х приащение ∆х х-  U-приращение
U-приращение
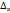 U=f(
U=f( 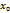 +
+ 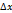 ,
, 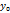 )- f(
)- f( 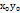 )
)
x-фикс, у-∆у=>∆yU=f( 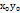 +∆y)- f(
+∆y)- f( 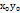 )
)
если же х и у получат приращение, тогда мы получим полное приращение
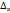 U=f(
U=f( 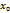 +
+ 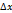 ,
, 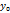 +∆у)- f(
+∆у)- f( 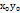 )
)
Опр:Число А наз-ся пределом ф-и U(x;y) в (.) 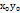 при стремлении точки х,у в (.) х0,у0 прооизвольным образом, если для всех Е>0 существует ∆>0:
при стремлении точки х,у в (.) х0,у0 прооизвольным образом, если для всех Е>0 существует ∆>0: 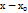 <∆ => f(x,y)=f(
<∆ => f(x,y)=f( 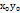 )<E
)<E
Опр:ф-я U=f(x,y) называется непрерывной в точке 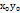 , если она определена в этой точке, и ее окрестности и
, если она определена в этой точке, и ее окрестности и  = f(
= f( 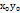 )
)
Опр:ф-я U непрерывна на множество Д, если она непрерывна в каждой точке этого множества
Св-ва непрерывной ф-и одного переменного без изменений переносится в данном случае
Билет2(ЧП фнп 1-го и высших порядков)
Опр:производная f( 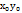 ) ф-и по переменной х в точке
) ф-и по переменной х в точке 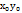 наз-ся ЧП по х от ф-и f(x,y) в точке
наз-ся ЧП по х от ф-и f(x,y) в точке 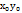
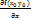 =
= 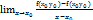
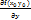 =
= 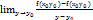
Опр:ЧП от прозводных 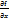 ,
, 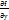 наз-сячп второго порядка
наз-сячп второго порядка
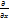 (
( 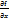 )=
)= 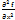
 (
( 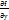 )=
)= 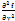
Смешанные ЧП: Теорема:если ф-я z=f(x,y) 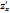 и
и 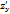 определены и непрерывны, то
определены и непрерывны, то 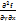 =
= 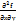 , т.е результат дифференцирования не зависит от пордка дифференцирования
, т.е результат дифференцирования не зависит от пордка дифференцирования
ЧП порядка n это ЧП от порядка (n-1)
Билет3 (дифференциал фнп 1-го и высших порядков)
Опр:ф-я z=f(x,y) в точке наз-ся дифференцируемой в М(х,у), если ее приращение в данной точке можно представить в виде ∆z=A∆x+B∆y+ 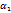 (∆x,∆y)∆x+
(∆x,∆y)∆x+ 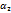 (∆x,∆y)∆y, где АиВ то числа независящие от ∆x,∆y соответственно
(∆x,∆y)∆y, где АиВ то числа независящие от ∆x,∆y соответственно 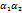 -это БМВ
-это БМВ
Дифференциалом ф-ии I-го порядка наз-ся гл.линейная часть е приращения. Это выражение так же наз-ся полным дифференциалом ф-ии z.
∆z=A∆x+B∆y-полный дифференциал
Т:если ф-я z=f(x,y) дифференциуема в точке (х,у), то z имеет ЧП и А= 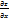 (x,y)
(x,y)
B= 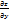 (x,y)
(x,y)
dz= 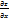 dx+
dx+ 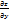 dy
dy
Т2:если ф-я z дифференцируема в точке (х,у), то она непрерывна в данной точке
Опр:полным дифференциалом 2-го порядка ф-и z наз-ся дифференциал ее дифференциала 1-го порядка т.е 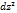 =d(dz)
=d(dz)
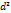 z=
z= 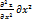 +2
+2 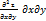 +
+ 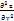 ∂
∂ 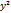
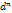 z=
z= 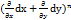 (z)
(z)
