Линейное однородное уравнение с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение с постоянными коэффициентами 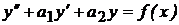(1)

и соответствующее ему однородное 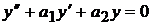, (2)

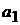где и 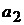– постоянные коэффициенты.

Найдем общее решение уравнения (2).

Будем искать решение уравнения (2) в форме .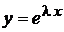

Тогда .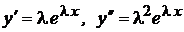

Подставляя это в уравнение (2), получим: .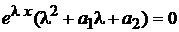

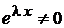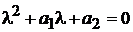Но так как , то (3)

Это уравнение по отношению к уравнению (2), называется характеристическим.

Если функция 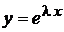есть решение уравнения (2), то 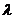должно быть корнем характеристического уравнения (3).

Рассмотрим три возможные случая:

1) корни уравнения (3) вещественны и различны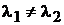

2) корни вещественны и равны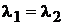

3) корни комплексные сопряженные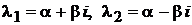

1 случай. 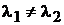и действительны.

В этом случае функци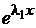и и 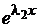будут решениями уравнения (2). Так как их отношение 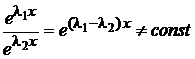, то эти решения линейно независимы и, следовательно, они составляют фундаментальную систему. А поэтому общее решение уравнения (2) в этом случае будет

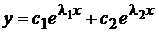(4)

Пример.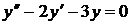

Характеристическое уравнение будет .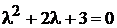

Его корни 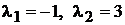. Общее решение будет .

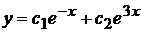2 случай.Корни равны .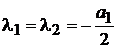

В этом случае имеем пока только одно решение 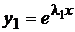. Покажем, что вторым решением будет 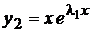. Действительно,

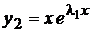
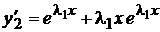
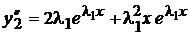
Подставим это в левую часть уравнения (2), тогда получим

,

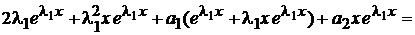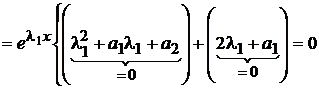
так как 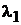есть корень уравнения (3), и потому, что 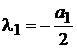. А это значит, что 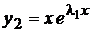есть решение (2), что и требовалось доказать.

Итак, мы имеем два решения 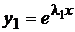и 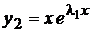. Они линейно независимы, следовательно, образуют фундаментальную систему решений. Поэтому общий интеграл будет .

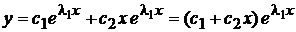Пример.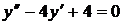

Характеристическое уравнение 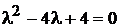. Корни .

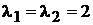Общее решение .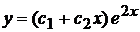

3 случай. Корни комплексные сопряженные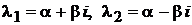

Следовательно, имеем два комплексных линейно независимых решения .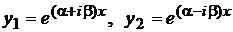

Общее решение будет .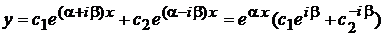

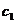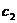Ясно, что иметь вещественное общее решение надо считать и комплексными числами. Выразим 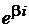и 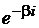по формулам Эйлера, тогда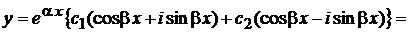

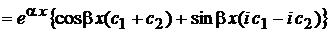
Положим здесь 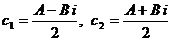. Тогда .

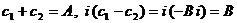Поэтому .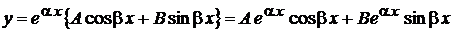

Таким образом, в случае комплексных сопряженных корней характеристического уравнения, уравнение (2) имеет два линейно независимых вещественных решения .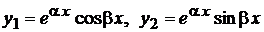

Общее решение .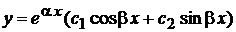

Пример.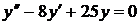

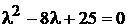
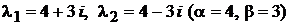
Общее решение .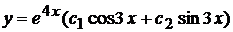

Линейное неоднородное уравнение с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение

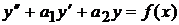, (1)

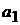где и 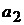– заданные постоянные коэффициенты.

Нам уже известно, что общее решение такого уравнения складывается из общего решения 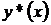, соответствующего однородного уравнения

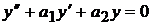(2)

и какого-нибудь частного решения 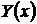уравнения (1), т.е. 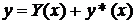. (3)

Как строить общее решение 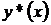однородного уравнения (2), мы рассмотрим в предыдущем параграфе. Поэтому теперь вопрос об общем решении уравнения (1) сведен лишь к вопросу о построении хотя бы какого-нибудь частного решения 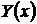уравнения (1). Вообще говоря, 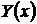можно, например, угадать. Но такой способ определения 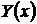очень ненадежен. Мы укажем сейчас точные способы, которые всегда приводят к цели.