Формула остроградского - лиувилля.

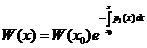(1).

Докажем эту формулу.

Производная от определителя n-го порядка (по строкам) равна сумме n определителей, получающихся из него поочерёдной заменой элементов каждой строки их производными. Так как все эти определители, кроме последнего, содержат две одинаковые строки и равны нулю, то в итоге будем иметь

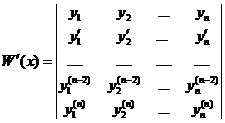(2).

Умножая элементы первых n-1 строк определителя (2) соответственно на 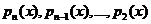и прибавляя их к элементам последней строки, учитывая, что L[y_i]= =0, получим 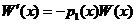(3).

Записывая решение уравнения (3) в форме Коши, получаем 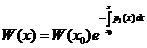(1).

Из формулы (1) видно, что если W(x₀)=0, то 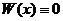во всём интервале (a,b).

Фундаментальная система решений (ФСР).

Совокупность любых n решений уравнения L[y] = 0, определённых и линейно независимых в интервале (a,b) называется фундаментальной системой решений в этом интервале. Чтобы система n решений была фундаментальной, необходимо и достаточно, чтобы W(x) этих решений был отличен от нуля хоть в одной точке интервала непрерывности коэффициентов уравнения L[y] = 0. Из определения ФСР следует, что фундаментальных систем может быть бесконечное множество.

Очевидно, что все решения ненулевые. Покажем, что ФСР уравнения L[y] = 0 всегда существует.

Теорема.

Если коэффициенты уравнения L[y] = 0 непрерывны в интервале (a,b), то существует ФСР, определённых в этом интервале.

Доказательство.

Возьмём 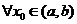и построим решение у₁ с начальными условиями при х = х₀ . Такое решение всегда существует и оно единственное на основании теоремы Пикара.

Аналогично построим у₂ с начальными условиями 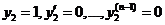при х=х₀.

И так далее: 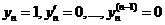при х=х₀.

Вронскиан построенных решений в точке х=х₀

Следовательно, y₁,..., y_n является ФСР на интервале (a,b).

Замечание. Построенная таким образом ФСР называется нормированной в точке х=х₀.

Существует только одна ФСР, нормированная в точке х = .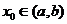

Построение общего решения.

Знание ФСР даёт возможность построить общее решение уравнения L[y] = 0.

Основная теорема.

Если y₁,..., y_n – фундаментальная система решений, то формула 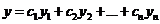(1) даёт общее решение уравнения L[y] = 0 в области 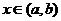, 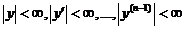(2).

(1) является решением уравнения L[y] = 0, т.к. это линейная комбинация решений y₁,..., y_n. Покажем, что это общее решение.

Продифференцируем выражение (1) n-1 раз.

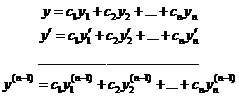(3).

Система (3) разрешима относительно 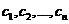в области (2), так как W(x)≠0. Поэтому, согласно определению общего решения уравнения n-го порядка, выражение (1) является общим решением уравнения L[y] = 0 в области (2).

Формула (1) содержит все решения. Как найти частное решение, удовлетворяющее следующим начальным условиям: 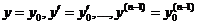(4) при х = 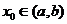. 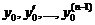- любые наперёд заданные числа.

Подставим значения (4) в систему (3), получим 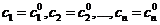и искомое решение имеет вид 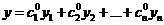(5).

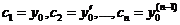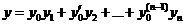Формула (5) имеет наиболее простой вид, если ФСР нормирована в точке Х₀. Тогда и (6).

Формулу (6) можно рассматривать как общее решение уравнения L[y] = 0 в форме Коши.

Пример. 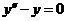(7),

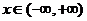
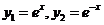- ФСР. Тогда согласно основной теореме 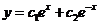- общее решение уравнения (7).

Система решений 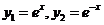не нормирована в точке х=0.

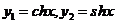- также является ФСР, но уже нормированной в точке х=0.

Тогда общее решение заданного уравнения можно записать в ви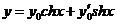де , где 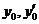- произвольные начальные условия в точке х=0.