Обыкновенные дифференциальные уравнения.
Обыкновенные дифференциальные уравнения.
Глава 1. Линейные дифференциальные уравнения n-го порядка.
ЛЕКЦИИ 1-2.
Введение.
Линейные уравнения – это наиболее разработанная часть теории диф. уравнений, так как они либо описывают реальные процессы, либо дают первое приближение и во многих случаях по этому приближению можно судить о характере изучаемого явления.
Линейным дифференциальным уравнением называется уравнение вида
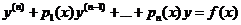 , (1)
, (1)
где рi(х), f(x) определены и непрерывны в интервале (а,b).
Тогда уравнение (1) имеет единственное решение у = у(х), удовлетворяющее начальным условиям:
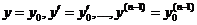 при х = х0, где
при х = х0, где  а
а 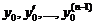 - любые заданные числа. Это решение определено и n раз дифференцируемо для
- любые заданные числа. Это решение определено и n раз дифференцируемо для 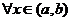 .
.
Особых решений уравнение (1) не имеет. Если f(x)≡0, то уравнение (1) называется однородным:
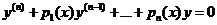 , (2).
, (2).
Для сокращения записи введём линейный дифференциальный оператор:
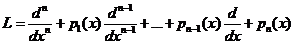 , (3).
, (3).
Тогда уравнение (1)можно записать в виде:
L[y] = f(x) (1), а однородное уравнение L[y] = 0 (2).
Запишем очевидные свойства оператора L:
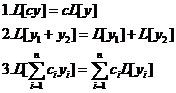
Определение. Функцию Z(x) = U(x) + iV(x) будем называть комплексной функцией от вещественной переменной х. U(x) u V(x) называются соответственно действительной и мнимой частями комплексной функции Z(x).
Теорема. Если комплексная функция у(х) является решением однородного уравнения (2), то её вещественная и мнимая части являются вещественными решениями этого уравнения.
Доказательство. y(x)=y1(x)+i y2(x) является решением уравнения (2).
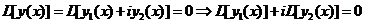 . Тогда
. Тогда 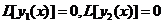 .
.
Пример. 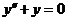
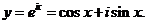
Понятие о линейной независимости функций.
Определение. Функции y1, y2,…, yn называются линейно независимыми в интервале (a,b), если между ними не существует соотношения вида: 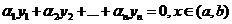 (1), где
(1), где 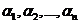 - постоянные числа, не равные нулю одновременно. В противном случае функции
- постоянные числа, не равные нулю одновременно. В противном случае функции 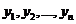 называются линейно зависимыми.
называются линейно зависимыми.
Очевидно, что если одна из функций 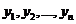 тождественно равна нулю в интервале (a,b), то эти функции линейно зависимы в (a,b).
тождественно равна нулю в интервале (a,b), то эти функции линейно зависимы в (a,b).
Пример 1. Функции 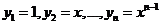 (2) линейно независимы в интервале
(2) линейно независимы в интервале 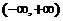 . Соотношение
. Соотношение  в котором не все
в котором не все 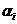 равны нулю, не может выполняться тождественно, так как уравнение n-1 степени не может иметь более чем n-1 корней.
равны нулю, не может выполняться тождественно, так как уравнение n-1 степени не может иметь более чем n-1 корней.
Пример 2. Пусть 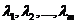 - различные числа. Тогда функции
- различные числа. Тогда функции
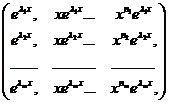 (3), где n1, n2,…, nm – целые неотрицательные числа, линейно независимы в интервале
(3), где n1, n2,…, nm – целые неотрицательные числа, линейно независимы в интервале 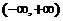 .
.
Пример 3. Пусть 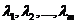 - различные числа. Тогда функции
- различные числа. Тогда функции
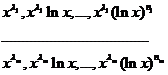 (4), где n1, n2,…, nm – целые неотрицательные числа, линейно
(4), где n1, n2,…, nm – целые неотрицательные числа, линейно
независимы в интервале 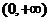 .
.
Пример 4. Функции 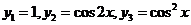 линейно зависимы в интервале
линейно зависимы в интервале 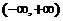 , так как при всех х справедливо соотношение
, так как при всех х справедливо соотношение 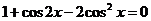 .
.
Пример 5. Функции 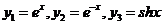 линейно зависимы в интервале
линейно зависимы в интервале 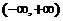 , так как
, так как 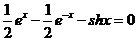 справедливо при всех х.
справедливо при всех х.
Построение общего решения.
Знание ФСР даёт возможность построить общее решение уравнения L[y] = 0.
Основная теорема.
Если y1,..., yn – фундаментальная система решений, то формула 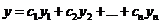 (1) даёт общее решение уравнения L[y] = 0 в области
(1) даёт общее решение уравнения L[y] = 0 в области 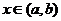 ,
, 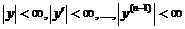 (2).
(2).
(1) является решением уравнения L[y] = 0, т.к. это линейная комбинация решений y1,..., yn. Покажем, что это общее решение.
Продифференцируем выражение (1) n-1 раз.
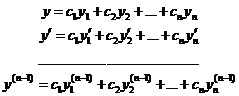 (3).
(3).
Система (3) разрешима относительно 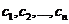 в области (2), так как W(x)≠0. Поэтому, согласно определению общего решения уравнения n-го порядка, выражение (1) является общим решением уравнения L[y] = 0 в области (2).
в области (2), так как W(x)≠0. Поэтому, согласно определению общего решения уравнения n-го порядка, выражение (1) является общим решением уравнения L[y] = 0 в области (2).
Формула (1) содержит все решения. Как найти частное решение, удовлетворяющее следующим начальным условиям: 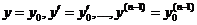 (4) при х =
(4) при х = 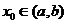 .
. 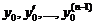 - любые наперёд заданные числа.
- любые наперёд заданные числа.
Подставим значения (4) в систему (3), получим 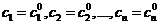 и искомое решение имеет вид
и искомое решение имеет вид 
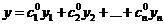 (5).
(5).
Формула (5) имеет наиболее простой вид, если ФСР нормирована в точке Х0. Тогда 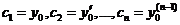 и
и 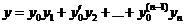 (6).
(6).
Формулу (6) можно рассматривать как общее решение уравнения L[y] = 0 в форме Коши.
Пример. 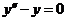 (7),
(7), 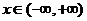
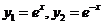 - ФСР. Тогда согласно основной теореме
- ФСР. Тогда согласно основной теореме 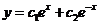 - общее решение уравнения (7).
- общее решение уравнения (7).
Система решений 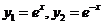 не нормирована в точке х=0.
не нормирована в точке х=0.
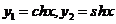 - также является ФСР, но уже нормированной в точке х=0.
- также является ФСР, но уже нормированной в точке х=0.
Тогда общее решение заданного уравнения можно записать в виде 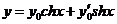 , где
, где 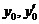 - произвольные начальные условия в точке х=0.
- произвольные начальные условия в точке х=0.
ЛЕКЦИЯ 3:
Метод Коши.
Укажем ещё один способ построения частного решения уравнения 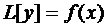 (1).
(1).
Пусть {zi} i=1,2..n – ФСР уравнения L[y]=0 (2)
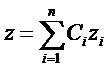 (3) – общее решение уравнения (2).
(3) – общее решение уравнения (2).
Построим решение уравнения (2), удовлетворяющее следующим начальным условиям :
z = 0, z/ = 0, …, z( n-2) =0, z( n-1) =1 при x = a, где "aÎ(a,b), xÎ(a,b).
Это решение 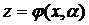 (5)
(5)
Причём 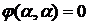 ,
, 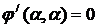 , …,
, …, 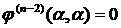 ,
, 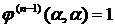 ,
,
где 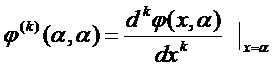 , (6)
, (6)
Докажем, что функция
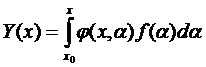 , (7)
, (7)
где " x0 Î (a,b).
является частным решением уравнения (1) с нулевыми начальными условиями, т.е. Y = 0, Y/ = 0, …, Y( n-1) =0, при x = x0.
Найдём значения производных функции Y(x):
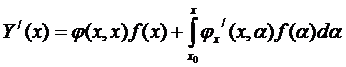 , первое слагаемое = 0,
, первое слагаемое = 0,
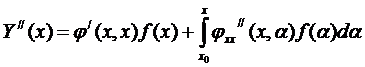 , первое слагаемое = 0, …… (8)
, первое слагаемое = 0, …… (8)
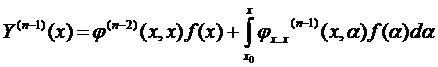 , первое слагаемое = 0,
, первое слагаемое = 0,
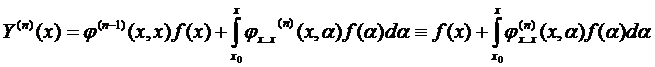 и
и 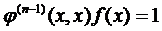 ,
,
Подставим выражение (8) в уравнение (1):
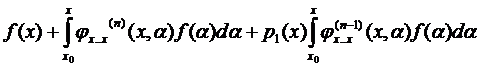 +……
+……
…+ 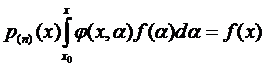 (9)
(9)
или
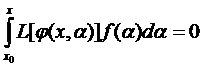 ,
,
Получим тождество для " x, x0 Î(a,b).
Итак, 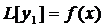 , x Î(a,b).
, x Î(a,b).
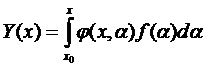 (7) –называется формулой Коши для неодноролного уравнения.
(7) –называется формулой Коши для неодноролного уравнения.
Очевидно, что Y(x0) = 0, Y/ (x0)= 0, …, Y( n-1) (x0)=0.
Таким образом 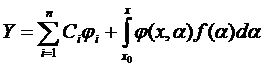 .
.
Пример:
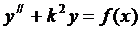
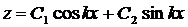 – общее решение однородного уравнения.
– общее решение однородного уравнения.
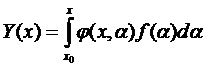
Найдём j (x,a)
z=0, z/=1 при x = a.
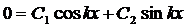
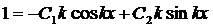 Þ
Þ 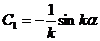
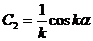
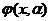
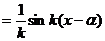
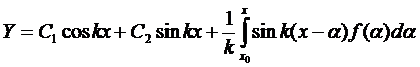
– oбщeе решение неоднородного уравнения.
ЛЕКЦИЯ 4:
Линейное уравнение Эйлера.
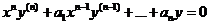 (1)
(1)
х=0 – особая точка уравнения (1)
Решение этого уравнения существует и единственно при 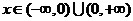 .
.
Будем рассматривать уравнение (1) при 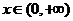 .
.
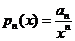 . Поэтому, согласно №14 :
. Поэтому, согласно №14 : 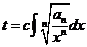 (2) ,
(2) , 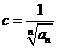 .
.
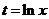 или
или 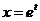 (3).
(3).
Тогда
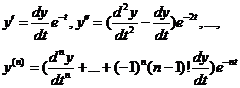 (4).
(4).
Подставляя (4) в уравнение (1), получаем однородное линейное уравнение n-го порядка с постоянными коэффициентами. Найдя общее решение и полагая в нём 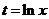 , мы получим общее решение уравнения Эйлера.
, мы получим общее решение уравнения Эйлера.
Пример 1. 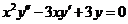 .
.
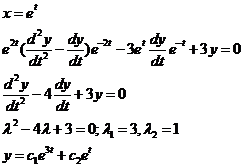
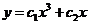 - общее решение однородного уравнения Эйлера.
- общее решение однородного уравнения Эйлера.
Пример 2. 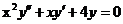
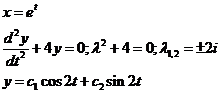
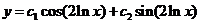 - общее решение уравнения Эйлера.
- общее решение уравнения Эйлера.
ЛЕКЦИЯ 6:
ЛЕКЦИЯ 7.
Построение общего решения.
Знание ФСР даёт возможность построения общего решения системы (2).
Основная теорема:
Если 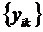 ,
, 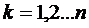 ,
, 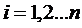 есть фундаментальная система решений в интервале
есть фундаментальная система решений в интервале 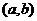 , то формулы
, то формулы 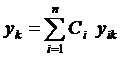 ,
, 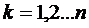 (22), где
(22), где
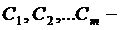 произвольные постоянные, дают общее решение системы в области
произвольные постоянные, дают общее решение системы в области 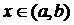 ,
, 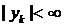 ,
, 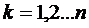 .
.
Действительно, система (22) разрешима относительно 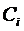 , так как
, так как 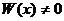 , кроме этого совокупность функций (22) является решением системы (2), что соответствует определению общего решения нормальной системы дифференциальных уравнений. Чтобы найти частное решение, удовлетворяющее условиям
, кроме этого совокупность функций (22) является решением системы (2), что соответствует определению общего решения нормальной системы дифференциальных уравнений. Чтобы найти частное решение, удовлетворяющее условиям 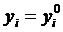 при
при 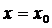 нужно подставить эти условия в систему (22).
нужно подставить эти условия в систему (22).
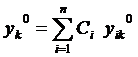 ,
, 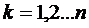 (230
(230
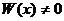 находим
находим 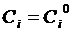 , откуда следует, что
, откуда следует, что 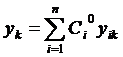 ,
, 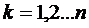 (24) – есть искомое решение.
(24) – есть искомое решение.
Теория устойчивости.
Рассмотрим систему 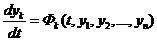 (k = 1,2,...,n) (1) с начальным условием
(k = 1,2,...,n) (1) с начальным условием 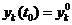 (k = 1,2,...,n), которое является результатом измерений и получено с некоторой погрешностью. Если сколь угодно малые изменения начальных данных способны сильно изменить решение, то такое решение не имеет никакого прикладного значения и даже приближенно не описывает изучаемое явление. Естественно возникает вопрос о нахождении условий, при которых достаточно малое изменение начальных данных вызывает сколь угодно малое изменение решения.
(k = 1,2,...,n), которое является результатом измерений и получено с некоторой погрешностью. Если сколь угодно малые изменения начальных данных способны сильно изменить решение, то такое решение не имеет никакого прикладного значения и даже приближенно не описывает изучаемое явление. Естественно возникает вопрос о нахождении условий, при которых достаточно малое изменение начальных данных вызывает сколь угодно малое изменение решения.
Если t меняется на конечном отрезке 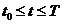 , то ответ уже получен теоремой о непрерывной зависимости решения от начальных значений.
, то ответ уже получен теоремой о непрерывной зависимости решения от начальных значений.
Определение. Решение 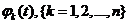 системы (1) называется устойчивым по Ляпунову, если для любого
системы (1) называется устойчивым по Ляпунову, если для любого 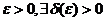 такое, что для любого
такое, что для любого 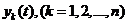 той же системы, начальные значения которого удовлетворяют неравенствам
той же системы, начальные значения которого удовлетворяют неравенствам 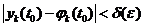 , (k = 1,2,...,n) (2).
, (k = 1,2,...,n) (2).
Для всех 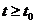 справедливы неравенства
справедливы неравенства 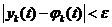 , (k = 1,2,...,n) (3) , т.е. близкие по начальным значениям решения остаются близкими для всех
, (k = 1,2,...,n) (3) , т.е. близкие по начальным значениям решения остаются близкими для всех 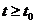 (можно писать
(можно писать 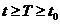 ).
).
Если при сколь угодно малом 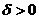 хотя бы для одного решения
хотя бы для одного решения 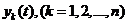 неравенство (3) не выполняется, то решение
неравенство (3) не выполняется, то решение 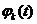 называется неустойчивым.
называется неустойчивым.
Если решение 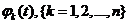 не только устойчиво, но, кроме этого, удовлетворяет условию
не только устойчиво, но, кроме этого, удовлетворяет условию 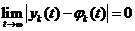 (4), это решение
(4), это решение 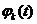 называется асимптотически устойчивым.
называется асимптотически устойчивым.
Пример. Исследовать на устойчивость решение уравнения 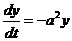 при условии
при условии 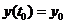 ,
, 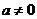
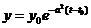 - асимптотически устойчиво, так как
- асимптотически устойчиво, так как 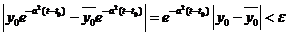 если
если 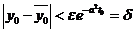 и
и 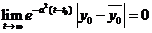 .
.
Сделаем замену в системе (1): 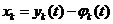 (5), (k = 1,2,...,n).
(5), (k = 1,2,...,n).
Тогда система (1) будет иметь вид: 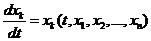 (6), и новыми неизвестными функциями
(6), и новыми неизвестными функциями 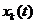 являются отклонения
являются отклонения 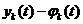 прежних неизвестных функций от
прежних неизвестных функций от 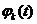 , определяющих устойчивость решения.
, определяющих устойчивость решения.
Тогда исследовать на устойчивость нужно будет тривиальное решение 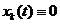 , (k = 1,2,...,n).
, (k = 1,2,...,n).
Сформулируем определение устойчивости для точки покоя: 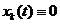 , (k = 1,2,...,n). Эта точка покоя системы (6) устойчива в смысле Ляпунова, если
, (k = 1,2,...,n). Эта точка покоя системы (6) устойчива в смысле Ляпунова, если 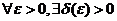 , что из неравенства
, что из неравенства 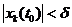 , (k = 1,2,...,n) следует
, (k = 1,2,...,n) следует 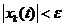 , (k = 1,2,...,n) при
, (k = 1,2,...,n) при 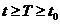 .
.
Второй метод Лагранжа.
Рассматривается система 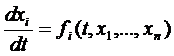 (1)
(1)
Теорема 1:
Если существует дифференцируемая функция 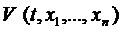 , называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат следующим условиям:
, называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат следующим условиям:
1) 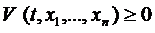 , причём
, причём 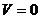 лишь при
лишь при 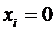 ,
,  .
.
2) 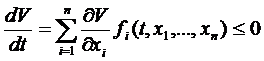 , при
, при 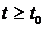 , то точка покоя
, то точка покоя 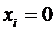
 системы (1) устойчива.
системы (1) устойчива.
Производная 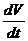 в условии 2) взята вдоль интегральных кривых системы (1).
в условии 2) взята вдоль интегральных кривых системы (1).
Доказательство:
Поверхности уровня в окрестности точки покоя, которая является точкой строгого минимума, являются замкнутыми и окружают точку покоя.
Рассмотрим поверхность уровня 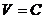 , которая целиком лежит в
, которая целиком лежит в 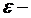 окрестности, т.е.
окрестности, т.е. 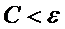 , но не проходит через начало координат. Выберем
, но не проходит через начало координат. Выберем 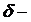 окрестность так, чтобы
окрестность так, чтобы 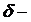 окрестность целиком лежала внутри поверхности
окрестность целиком лежала внутри поверхности 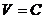 . Если начальная точка с координатами
. Если начальная точка с координатами 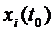 ,
,  находилась в
находилась в 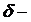 окрестности, то
окрестности, то 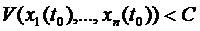 , то при
, то при 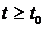 точка траектории, которая проходит через точку
точка траектории, которая проходит через точку 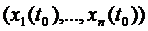 не выйдет за пределы
не выйдет за пределы 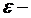 окрестности начала координат в силу условия 2) теоремы.
окрестности начала координат в силу условия 2) теоремы.
Теорема 2: (т. Ляпунова для ассимптотичной устойчивости)
Если существует дифференцируемая функция Ляпунова 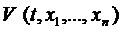 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) 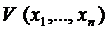 имеет строгий минимум в начале координат
имеет строгий минимум в начале координат 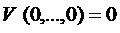 .
.
2) производная функция 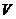 , вычисляемая вдоль интегральных кривых системы (1):
, вычисляемая вдоль интегральных кривых системы (1):
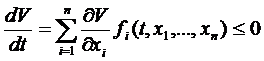 , причём вне сколь угодно малой окрестности начала координат, т.е. при
, причём вне сколь угодно малой окрестности начала координат, т.е. при 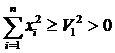 ,
, 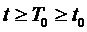 производная
производная 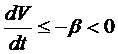 , где
, где 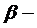 постоянная, то точка покоя
постоянная, то точка покоя 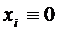 ,
,  системы (1) асимптотически устойчива.
системы (1) асимптотически устойчива.
Доказательство:
Условия теоремы выполнены, то если 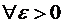 можно выбрать
можно выбрать 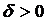 , что траектория, начальная точка которой не выйдет из
, что траектория, начальная точка которой не выйдет из 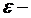 окрестности начала координат.
окрестности начала координат.
Вдоль траектории функция 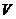 монотонно убывает с возрастанием
монотонно убывает с возрастанием 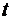 . Следовательно, существует
. Следовательно, существует 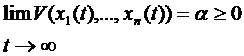
Надо показать, что 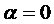 . Откуда будет следовать, что
. Откуда будет следовать, что 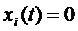 ,
,  .
.
Первое условие теоремы 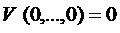 только в начале координат.
только в начале координат.
Допустим, что 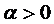 .
.
Тогда 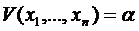 возьмём за
возьмём за 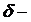 окрестность, но здесь
окрестность, но здесь 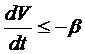 , проинтегрируем это неравенство от
, проинтегрируем это неравенство от 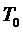 до
до 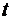 :
:
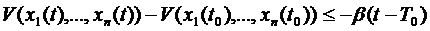
или
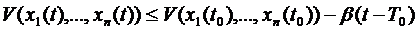
При достаточно большом 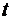 правая часть отрицательна и , следовательно,
правая часть отрицательна и , следовательно, 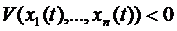 , что противоречит условию 1).
, что противоречит условию 1).
Пример 1:
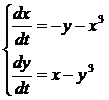 ,
, 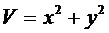
1) 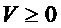 ,
, 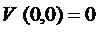
2) 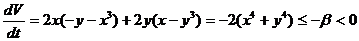
Решение 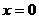 ,
, 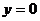 асимптотически устойчиво.
асимптотически устойчиво.
Пример 2:
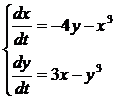 ,
, 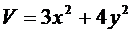
1) 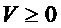 ,
, 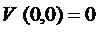
2) 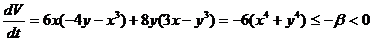
Решение 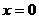 ,
, 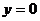 асимптотически устойчиво.
асимптотически устойчиво.
Исследование проблемы устойчивости по первому приближению.
При исследовании на устойчивость точки покоя 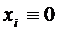 ,
,  системы
системы 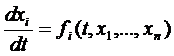 (1), где
(1), где 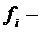 дифференцируемая окрестности начала координат функция.
дифференцируемая окрестности начала координат функция.
Применяется следующий метод:
Систему (1) представляют в окрестности начала координат:
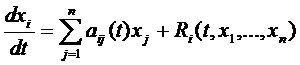 ,
,  (2)
(2)
Система 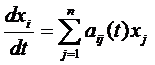 ,
,  (3)
(3)
Называется системой первого приближения для системы (1).
Теорема 3:
Если система (2) стационарна в первом приближении, все числа 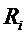 ,
,  в достаточно малой окрестности начала координат при
в достаточно малой окрестности начала координат при 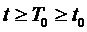 удовлетворяют неравенствам:
удовлетворяют неравенствам:
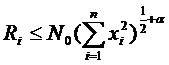 , где
, где 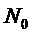 и
и 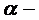 постоянные.
постоянные.
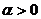 и все корни характеристического уравнения:
и все корни характеристического уравнения:
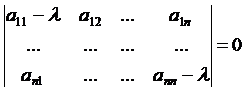 (4)
(4)
имеют отрицательные действительные части, то тривиальное решение 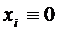 ,
,  системы (1) асимптотически устойчиво.
системы (1) асимптотически устойчиво.
Теорема 4:
Если система (2) стационарна в первом приближении, все функции 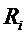 ,
,  удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (4) имеет положительную действительную часть, то точка покоя
удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (4) имеет положительную действительную часть, то точка покоя 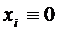 ,
,  системы (2) неустойчива.
системы (2) неустойчива.
В критическом случае, когда действительная часть и хотя бы одного корня равна нулю, на устойчивость начинают влиять нелинейные члены 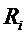 и исследование на устойчивость по первому приближению невозможно.
и исследование на устойчивость по первому приближению невозможно.
Пример 1:
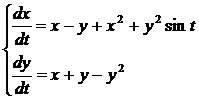
Нелинейные члены удовлетворяют условиям теорем 3. и 4. Исследуем на устойчивость точку покоя 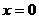 ,
, 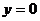 .
.
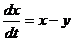 ,
, 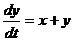
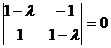 ,
, 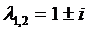
Решение 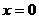 ,
, 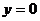 неустойчиво.
неустойчиво.
Пример 2:
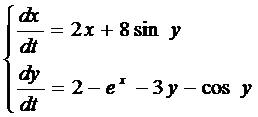
Разлагая 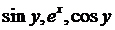 по формулам Тейлора, получим:
по формулам Тейлора, получим:
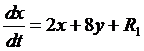 ,
, 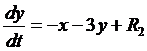 ,
,
где 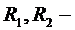 удовлетворяют теоремам 4. и 5.
удовлетворяют теоремам 4. и 5.
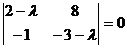 ,
, 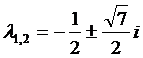
Решение 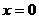 ,
, 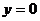 асимптотически устойчиво.
асимптотически устойчиво.
ЛЕКЦИЯ 13.
Теорема о существовании и единственности решения линейного интегрального уравнения Фредгольма 2-го рода с параметром.
Рассмотрим уравнение 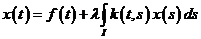 (1)
(1)
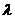 – постоянное число, может быть комплексным.
– постоянное число, может быть комплексным.
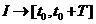 ;
; 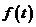 и
и 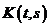 - непрерывные функции и, следовательно, ограничены, т.е.
- непрерывные функции и, следовательно, ограничены, т.е. 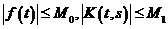 . (2)
. (2) 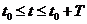 ,
, 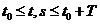
Будем доказывать существование и единственность решения уравнения (1), используя принцип сжатых изображений.
Принцип сжатых изображений.
Теорема. Если в полном метрическом пространстве М задан оператор А, удовлетворяющий следующим условиям:
1) Оператор А переводит точки пространства М в точки того же пространства, т.е. 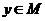 , то
, то 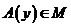 ;
;
2) Оператор сближает точки, т.е. 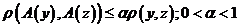
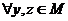 ;
; 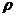 - расстояние между точками,
- расстояние между точками, 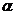 не зависит от выбора точек
не зависит от выбора точек 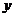 и z.
и z.
Тогда существует единственная неподвижная точка 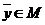 , что
, что 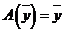 , и эта точка может быть найдена методом последовательных приближений, т.е.
, и эта точка может быть найдена методом последовательных приближений, т.е. 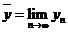 , где
, где 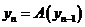 (3), причем
(3), причем 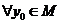 .
.
Пояснения к теореме.
Ι. Пространство М называется метрическим, если в нём определена функция 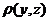 , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1. 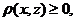
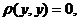
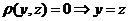 ;
;
2. 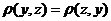 ;
;
3. 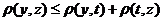 .
.
Здесь, 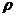 называется расстоянием.
называется расстоянием.
ΙΙ. Метрическое пространство называется постоянным, если любая фундаментальная последовательность точек пространства М сходится в этом пространстве. Последовательность 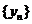 называется фундаментальной, если для
называется фундаментальной, если для 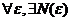 , что для
, что для 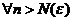 и для
и для 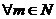 :
: 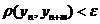 .
.
Доказательство.
Покажем, что 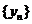 (3) - фундаментальная последовательность.
(3) - фундаментальная последовательность.
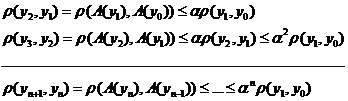 (4)
(4)
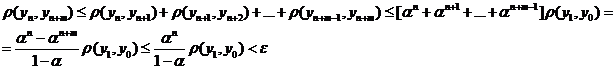
Итак, 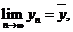
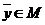 (в силу полноты пространства М). Покажем, что
(в силу полноты пространства М). Покажем, что 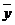 неподвижна.
неподвижна.
Пусть 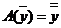 .
.
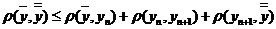
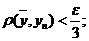
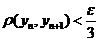 так как последовательность фундаментальная.
так как последовательность фундаментальная.
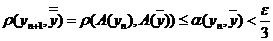 .
.
Итак, 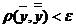 . Следовательно,
. Следовательно, 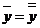
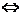
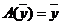 .
.
Докажем, что эта точка единственная. Предположим, что есть ещё одна z такая, что A(z) = z.
Тогда  , что противоречит второму условию теоремы.
, что противоречит второму условию теоремы.
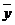 - единственная точка.
- единственная точка.
Применим принцип сжатых отображений для доказательства теоремы о существовании и единственности решения уравнения (1).
Рассмотрим функциональное пространство непрерывных функций, заданных на промежутке I. Под расстоянием на этом пространстве между двумя любыми элементами этого пространства будем понимать 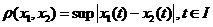 (5).
(5).
Пространство является полным. Т.е. фундаментальная последовательность имеет предел, принадлежащий этому пространству:
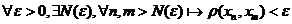 .
.
В полном метрическом пространстве существует единственная неподвижная точка у оператора сжатых отображений. Ах = х.
Обозначим: 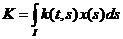 - интегральный оператор.
- интегральный оператор.
Тогда 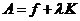 (6) и уравнение (1) будет иметь вид х = Ах (7). Если мы докажем, что А – оператор сжатых отображений, то тем самым будет доказано, что уравнение (1) имеет единственное решение.
(6) и уравнение (1) будет иметь вид х = Ах (7). Если мы докажем, что А – оператор сжатых отображений, то тем самым будет доказано, что уравнение (1) имеет единственное решение.
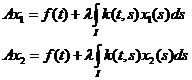 (8)
(8)
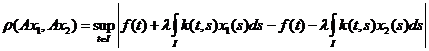 .
.
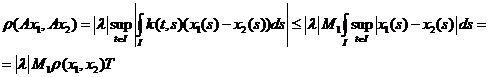 (9).
(9).
Если сделать 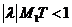 , то оператор будет сжимающим, т.е.
, то оператор будет сжимающим, т.е. 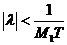 (10). Параметр с таким условием называется малым.
(10). Параметр с таким условием называется малым.
Уравнение Фредгольма (1) с условием (10) имеет единственное решение. Если Т – переменная величина, т.е. уравнение (1) есть уравнение Вольтера, то 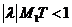 можно сделать за счёт малости интервала по t. Уравнение Вольтера имеет единственное решение на достаточно малом промежутке.
можно сделать за счёт малости интервала по t. Уравнение Вольтера имеет единственное решение на достаточно малом промежутке.
Рассмотрим однородное уравнение Фредгольма 2-го рода: 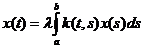 (11).
(11).
Если 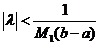 , то существует только тривиальное, нулевое решение.
, то существует только тривиальное, нулевое решение.
Те значения λ, при которых однородное уравнение (11) имеет решения, отличные от нулевого, называются собственными решениями.
Замечание.
Так как уравнение Вольтера имеет единственное решение при любом λ, то уравнение Вольтера не имеет собственных значений и собственных решений.
ЛЕКЦИЯ 14:
Вариация и её свойства.
Определение 2:
Приращением или вариацией 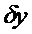 аргумента
аргумента 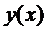 функционала
функционала 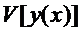 называется разность между двумя функциями
называется разность между двумя функциями 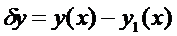 , где
, где 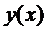 меняется произвольно в некотором классе функций.
меняется произвольно в некотором классе функций.
Определение 3:
Функционал 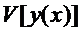 непрерывен при
непрерывен при 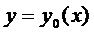 в смысле близости
в смысле близости 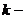 ого порядка, если
ого порядка, если 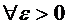
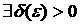 такое, что имеет место неравенство
такое, что имеет место неравенство
 при
при
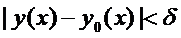 ,
,
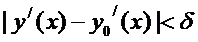 ,
,
…
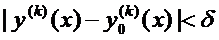 .
.
Функция 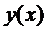 берётся из класса функций, на котором функционал
берётся из класса функций, на котором функционал 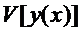 определён.
определён.
Определение 4:
Функционал называется линейным 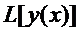 , если выполняются следующие условия:
, если выполняются следующие условия:
1. 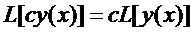 , где
, где 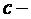 постоянная.
постоянная.
2 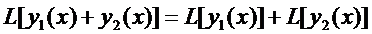
Например, 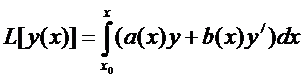 .
.
Определение 5:
Если приращение функционала 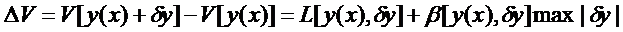 представимо в таком виде, где
представимо в таком виде, где 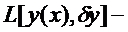 линейный по отношению к
линейный по отношению к 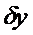 функционал и
функционал и 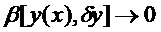 при
при 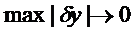 , то линейная по отношению к
, то линейная по отношению к 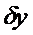 часть приращения функционала, т.е.
часть приращения функционала, т.е. 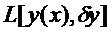 называется вариацией функционала и обозначается
называется вариацией функционала и обозначается 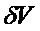 .
.
Итак, вариация функционала – это главная, линейная по отношению к 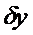 часть приращения функционала.
часть приращения функционала.
При исследовании функционалов, вариация играет ту же роль, что и производная при исследовании функций.
Вообще говоря, упрощения исследования функционалов дают почти эквивалентное определение вариации функционала.
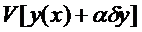 по
по 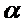 при
при 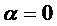 , т.е.
, т.е. 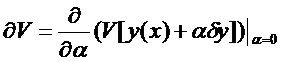 .
.
Действительно, производная от 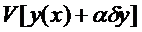 по
по 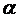 при
при 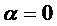 равна:
равна:
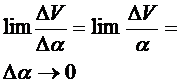
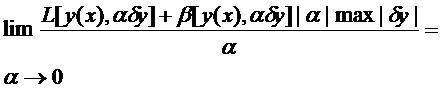
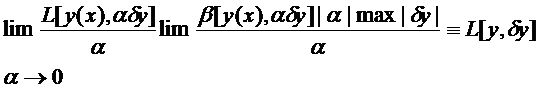 .
.
Так как 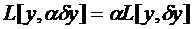 , а
, а 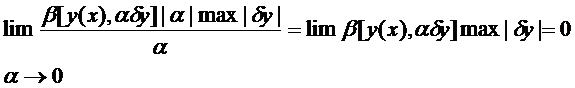
Если существует вариация в смысле главной части приращения функционала, то существует и вариация в смысле производной по параметру при 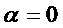 . Второе определение несколько шире первого, так как не всегда можно выделить главную линейную часть приращения функционала.
. Второе определение несколько шире первого, так как не всегда можно выделить главную линейную часть приращения функционала.
Определение 6:
Функционал 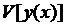 достигает на кривой
достигает на кривой 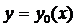 максимума(минимума), если значения функционала
максимума(минимума), если значения функционала 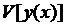 на любой близкой от
на любой близкой от 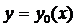 кривой, больше(не меньше), чем
кривой, больше(не меньше), чем 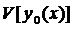 , т.е.
, т.е. 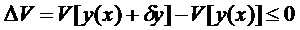 .
.
Если 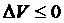 (
( 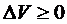 ) и
) и 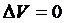 только при
только при
