Систематический циклический код

Построение кодового полинома путем перемножения информационного и порождающего полиномов приводит к не систематическому кодовому слову, в котором отсутствует явное разделение информационных и проверочных символов.

Для того чтобы прийти к систематической форме кодового слова необходимо осуществить некоторое согласование между информационным и кодовым полиномами. Пусть 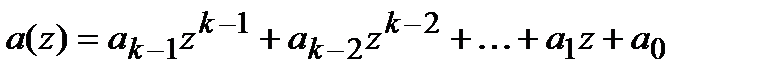– информационный полином, а 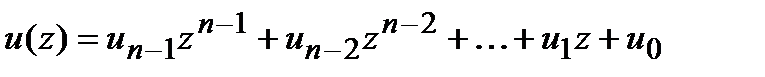– кодовый. Систематическое правило кодирование предполагает получение кодового полинома в таком виде, чтобы коэффициенты при старших степенях полинома соответствовали информационным символам. Данное требование достигается путем умножения информационно полинома на многочлен :

,

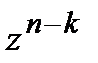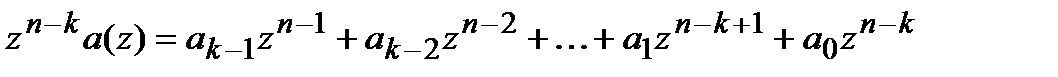что эквивалентно сдвигу информационного слова на 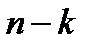позиций вправо и добавления слева аналогично числа нулей.

Поскольку любой кодовый полином должен делиться на порождающий полином , из последнего соотношения необходимо вычесть остаток 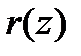, получаемый в результате деления 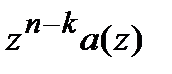на , т.е. 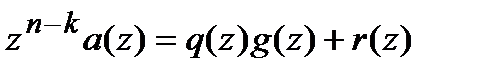. В итоге, кодовое слово в систематической форме представимо в виде

.

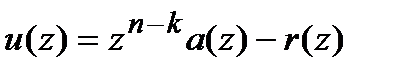Коды Рида-Соломона

Остановимся здесь на важном частном случае циклического кода – коде Рида-Соломона (РС).

Коды РС являются недвоичными циклическими кодами, символы кодовых слов которых берутся из конечного поля 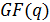. Здесь 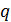степень некоторого простого числа, 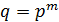, 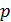–простое.

Кодовые слова РС-кода отображаются в виде многочленов

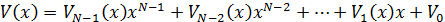
где 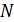- длина кода; 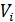- -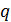ичные коэффициенты (символы кодовых слов), которые могут принимать любое значение из 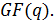Коды РС являются максимальными, т.к. при длине кода 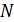и информационной последовательности 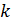они обладают наибольшим кодовым расстоянием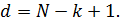

Порождающим многочленом 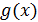РС-кода является делитель двучлена x^N+1 степени меньшей 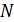с коэффициентами из 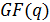при условии, что элементы этого поля являются корнями 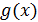. Здесь 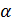- примитивный элемент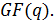

На основе этого определения, а также теоремы Безу, выражение для порождающего многочлена РС-кода будет иметь вид

)

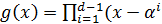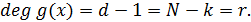
В РС-кодах принадлежность кодовых слов данному коду определяется выполнением d-1 уравнений в соответствии с выражением,

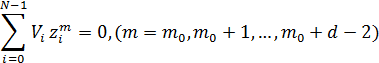где 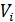- символы-коэффициенты из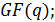
z₀, z₁... z_N-1 - ненулевые элементы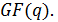

Элементы z₀, z₁... z_N-1 называются локаторами, т.е. указывающими на номер позиции символа кодового слова. Например, указателем 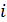- позиции является локатор 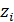или элемент aⁱ 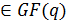. Так как все локаторы должны быть различны и причем ненулевыми, то их число в 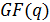равно 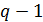. Следовательно, такое количество символов должно быть в кодовых словах кода.Поэтому обычно длина РС-кода определяется из выражения .

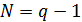Приведем основные свойства РС-кодов.

1. Циклический сдвиг кодовых слов, символы которых принимают значение из 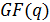, порождает новые кодовые слова этого же кода.

2. Сумма по 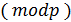двух и более кодовых слов дает кодовое слово, принадлежащее этому же коду.

3. В РС-коде, исправляющем t_u ошибок, порождающий многочлен определяется из выражения.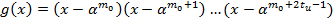

Обычно m₀ принимают равным 1. Однако, с помощью разумного выбора значения m₀, иногда можно упростить схему кодера.