Раздел 1. ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
Раздел 1. ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
1.1 Основные определения
Повышение требований к скорости и достоверности передачи информации, увеличение протяженности линий связи приводит к необходимости принятия специальных мер, направленных на уменьшение вероятности возникновения ошибок в процессе передачи. Одним из возможных решений указанной задачи служит помехоустойчивое кодирование. Подпомехоустойчивыми понимаются коды, позволяющие обнаруживать и исправлять ошибки, возникающие при передаче из-за воздействия помех. Суть данной процедуры состоит во введении в информационный поток специальным образом дополнительных символов, в результате чего каждому блоку из k информационных бит сопоставляется n символьная последовательность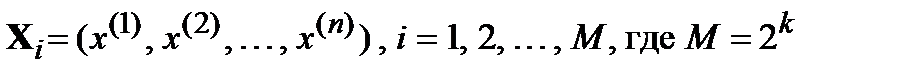 
– число возможных сообщений. Поскольку 
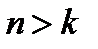, то не все последовательности длины n используются при кодировании M сообщений. Комбинации символов, используемые для отображения информационных блоков или сообщений, называют разрешенными комбинациями или кодовыми последовательностями (словами), тогда как остальные – запрещенными. Вся совокупность кодовых слов 
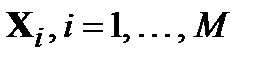образует код, для обозначения которого обычно говорят «код объема 
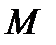длины 
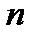». Множество символов, из которых составляются кодовые слова, называется алфавитом кода, а число различных символов в алфавите – основанием кода, или объемом (мощностью) алфавита.
Именно введение дополнительных символов и позволяет осуществить нейтрализацию влияния канальных помех. Появление указанной способности объясняется введением добавочных (проверочных) символов в кодовом слове, т.е. за счет введения избыточности.
Классификация кодов
Существует несколько подходов к классификации кодов, мы приведем основные из них:
В зависимости от позиций, с которых рассматривается процедура кодирования, классификация кодов может осуществляться различным образом. Простейшим вариантом может служить классификация по размеру алфавита кода. Если символы кода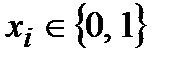 
или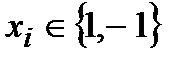 
, то код называется двоичным или бинарным соответственно. Если же алфавит кода содержит 
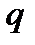символов, соответствующий ему код носит наименование 
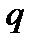–ичного. В данной работе основное внимание будет концентрироваться на двоичных или бинарных кодах.
Классификация кодов может быть осуществлена и по возможности выделения информационных символов в кодовом слове. Коды, в которых, как правило, первые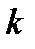 
позиций занимают информационные символы, называются систематическими кодами. В противном случае – несистематическимими.
Коды можно классифицировать и по способу противодействия искажениям в канале распространения. Коды, позволяющие исправлять ошибки, получили наименование исправляющих ошибки, тогда как коды только их фиксирующие, называются кодами, обнаруживающими ошибки. Нередко коды, обнаруживающие и исправляющие ошибки, называют контролирующими ошибки.
В заключении также отметим, что часто термину код предшествует слово, определяющее либо алгоритм его конструирования, либо имя ученого, открывшего правило формирования: линейные, циклические, полиномиальные коды, коды Хэмминга и др.
МНОГОЧЛЕНЫ НАД ПОЛЯМИ ГАЛУА
Расширенные конечные поля
Теперь у нас есть все необходимые сведения, чтобы расширить поле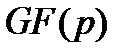 
до поля 
( 
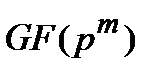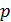– простое число).Как уже известно, существуют конечные поля только порядка 
( 
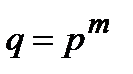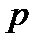– простое, 
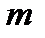– натуральное числа). Простое поле 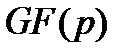порядка 
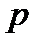может трактоваться как множество остатков от деления целых чисел на : 
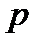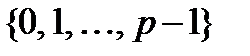с операциями сложения и умножения по модулю 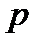. Аналогичным образом расширенное поле 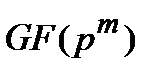порядка 
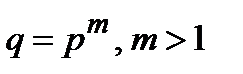, может трактоваться как множество остатков от деления полиномов над 
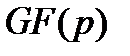на некоторый неприводимый полином 
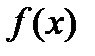степени 
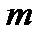с операциями сложения и умножения по модулю 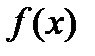. Другими словами, поле 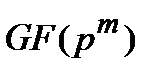содержит все полиномы над полем 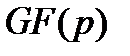степени не выше 
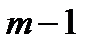с общепринятыми операциями сложения и умножением, осуществляемым в два этапа – вначале производится обычное умножение полиномов, а затем удерживается только остаток от деления полученного произведения на полином .
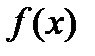Отметим, что среди полиномов степени не выше 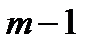присутствуют и полиномы нулевой степени, т.е. элементы простого поля 
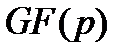, сложение и умножение которых, осуществляются по правилам 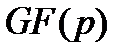. Это означает, что простое поле 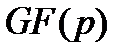полностью содержится в расширенном 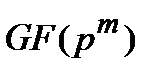, или, другими словами, 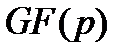является подполем 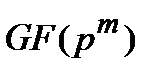. Для поля 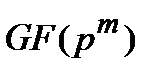порядок его простого подполя 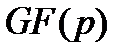называется характеристикой поля 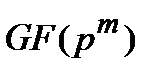. Например,любое расширенное поле 
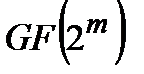является полем характеристики 2, вследствие чего вычисление коэффициентов полиномов, рассматриваемых как элементы поля 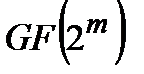, осуществляется по модулю два. В частности, для любого 
, 
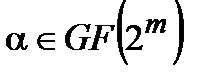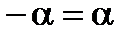, поскольку 
.
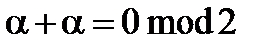Линейные коды
Рассмотрим множество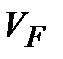 
, состоящее из 
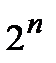всех возможных 
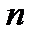–компонентных векторов 
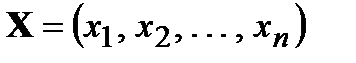, элементы которого 
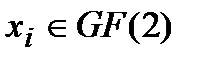. Очевидно, что 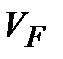образует 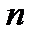–мерное векторное пространство. Выберем в этом пространстве 
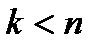линейно независимых векторов 
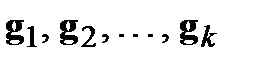, что всегда возможно, поскольку в 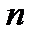–мерном пространстве всегда существуют 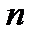линейно независимых векторов. Построим множество 
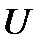, содержащее 
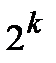векторов, образованных как линейная комбинация 
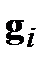вида:
.
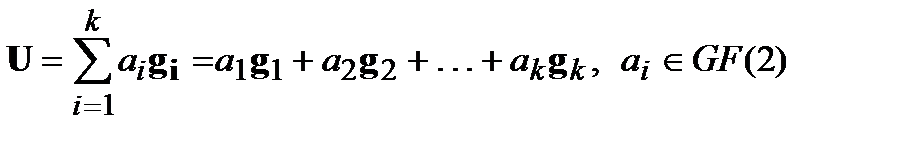Непосредственной проверкой легко убедиться, что множество 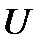замкнуто по сложению векторов и умножению их на скаляр из 
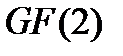, и, следовательно, 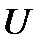является векторным пространством, т.е. подпространством 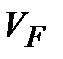. Это подпространство имеет размерность 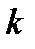и непосредственно является той конструкцией, которую назовем линейным кодом.
Двоичным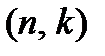 
линейным кодом является любое 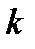–мерное подпространство пространства векторов длины 
.
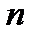Поскольку подпространство содержит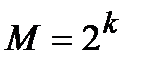 
кодовых слов, то 
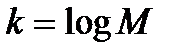есть ни что иное, как число информационных символов, переносимых кодом, а 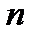– длина кода. Наряду с обозначением кода как 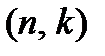код, встречается и другое, в котором используется еще один его параметр – кодовое расстояние: 
.
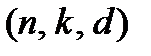Коды Рида-Соломона
Остановимся здесь на важном частном случае циклического кода – коде Рида-Соломона (РС).
Коды РС являются недвоичными циклическими кодами, символы кодовых слов которых берутся из конечного поля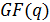 
. Здесь 
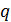степень некоторого простого числа, 
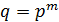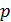, –простое.
Кодовые слова РС-кода отображаются в виде многочленов
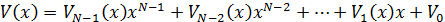
где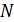 
- длина кода; 
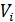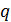- -ичные коэффициенты (символы кодовых слов), которые могут принимать любое значение из 
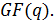Коды РС являются максимальными, т.к. при длине кода 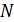и информационной последовательности 
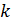они обладают наибольшим кодовым расстоянием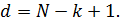 
Порождающим многочленом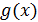 
РС-кода является делитель двучлена xN+1 степени меньшей 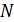с коэффициентами из 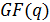при условии, что элементы 
этого поля являются корнями 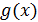. Здесь 
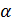- примитивный элемент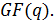
На основе этого определения, а также теоремы Безу, выражение для порождающего многочлена РС-кода будет иметь вид
)
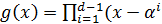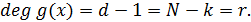
В РС-кодах принадлежность кодовых слов данному коду определяется выполнением d-1 уравнений в соответствии с выражением,
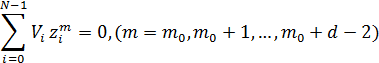где 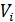- символы-коэффициенты из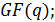 
z0, z1... zN-1 - ненулевые элементы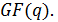 
Элементы z0, z1... zN-1 называются локаторами, т.е. указывающими на номер позиции символа кодового слова. Например, указателем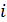 
- позиции является локатор 
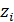или элемент ai 
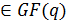. Так как все локаторы должны быть различны и причем ненулевыми, то их число в 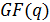равно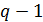 
. Следовательно, такое количество символов должно быть в кодовых словах кода.Поэтому обычно длина РС-кода определяется из выражения 
.
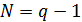Приведем основные свойства РС-кодов.
1. Циклический сдвиг кодовых слов, символы которых принимают значение из 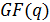, порождает новые кодовые слова этого же кода.
2. Сумма по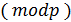 
двух и более кодовых слов дает кодовое слово, принадлежащее этому же коду.
3. В РС-коде, исправляющем tu ошибок, порождающий многочлен определяется из выражения.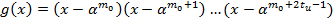 
Обычно m0 принимают равным 1. Однако, с помощью разумного выбора значения m0, иногда можно упростить схему кодера.
Теорема 4.1.4.
(i). Элемент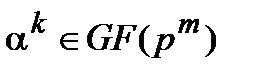 
является корнем полинома 
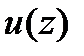тогда и только тогда, когда k–й частотный компонент 
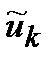равен нулю.
(ii). Элемент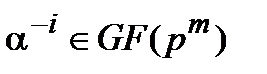 
является корнем многочлена 
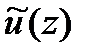тогда и только тогда, когда i–й временной компонент 
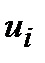равен нулю.
Доказательство утверждения (i) очевидно, поскольку из непосредственной подстановки корня в полино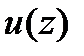м имеем
.
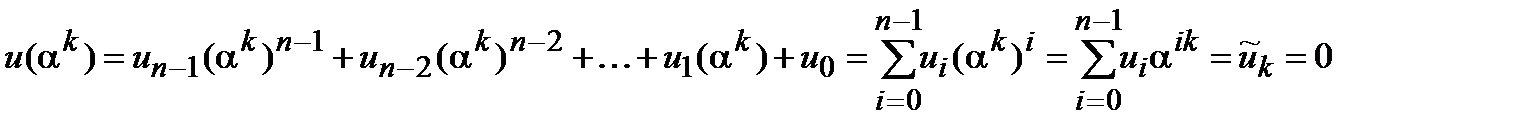Аналогичным образом доказывается и утверждение (ii).
На основании приведенной теоремы можно сделать следующее заключение. Поскольку любой кодовый многочлен содержит в качестве множителя порождающий многочлен, то корни порождающего полинома являются и корнями кодового. Тогда, согласно теореме 4.1.4, корням порождающего многочлена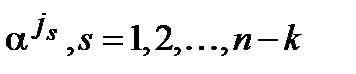 
будут соответствовать нулевые спектральные компоненты кодовых слов на позициях 
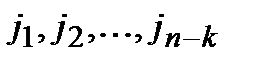. Следовательно, можно дать следующее альтернативное определение циклического кода. Циклическим кодом 
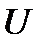называется множество таких слов над конечным полем 
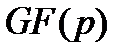, у которых все спектральные компоненты, принадлежащие заданному множеству т.н. проверочных частот 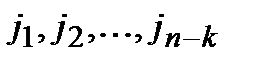равны нулю
Кодовое слово кода Р-С длины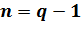 
и его спектр лежат в одном поле 
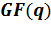.Кодирование кода Рида-Соломона в частной области можно осуществить следующим образом: какие либо 
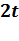последовательных координат полагаются равными нулю, в остальных 
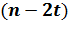координатах записываются информационные символы. Например, информационный вектор может быть такой: 
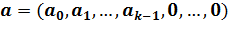.Кодовый вектор, соответствующий информационному вектору, определяется как ДПФ вектора 
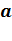с ядром α. Координаты кодового вектора задаются по правилу 
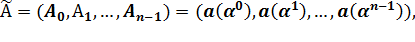так как каждая компонента 
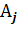вычисляется как значение многочлена a(x) в точке 
: 
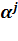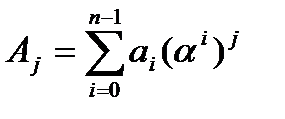. Если a(x) – многочлен из информационной области, A(x) – многочлен из кодовой области, тогда дискретное преобразование Фурье с ядром α (прямое) переводит многочлен из информационной области в кодовую, а дискретное преобразование Фурье с ядром 
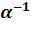(обратное) переводит многочлен из кодовой области в информационную 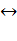а(х) 
А(х),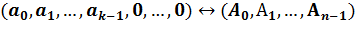 
.
ЗАКЛЮЧЕНИЕ
На основании китайской теоремы об остатках получен результат, существенно понижающий вычислительную сложность ДПФ. Приведены формулы для трехмерного преобразования Фурье поле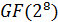 
. Построены алгоритмы быстрого преобразование Фурье (БПФ) длин 3, 5 и 17 на основе алгоритма Рейдера и алгоритма Винограда вычисления циклической свертки. Показана эквивалентность между вычислением ДПФ простой длины и вычислением циклической свертки.
На основании трехмерного преобразования Фурье построеныукороченные преобразования длин 15, 51, 85, которые рационально применять, когда не требуется кодировать слова длины 255. Показана эквивалентность между укорочением преобразования и переходом на соответствующую ему подгруппу мультипликативной группы поля.
В приложении представлен программный комплекс, реализующий построение поля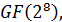 
основные операции в этом поле, вычисление значения произвольного многочлена в любой точке поле, вычисление ДПФ, ОДПФ, трехмерного преобразования Фурье и БПФ длин 255,85,51,15,17,5,3, кодирование кодом Рида-Соломона в частотной области.
Проведенные вычислительные эксперименты показали практическую эффективность перехода от ДПФ к трехмерному преобразованию: если на вычисление ДПФ длины 255 затрачивается примерно 300-350 мс машинного времени, то трехмерное преобразование занимает от 20 до 35 мс. При этом на вычисление БПФ длины 255 затрачивается всего 13-17 мс.
Разработанный программный комплекс можно применять при создании систем хранения и передачи данных с повышенной надежностью. Удобный и наглядный пользовательский интерфейс интуитивно понятен и не вызовет проблем у разработчиков этих систем.
Языком реализации выбранBorlandDelphiEnterprise 2007.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Берлекэмп Э. Р. Алгебраическая теория кодирования. М.: Мир, 1971
2. Nussbaumer H. J. Fast Fourier Transform and Convolution Algorithms. – Springer-Verlag: Berlin, Heidelberg, New York, 1981.
3. Помехоустойчивое кодирование и надежность ЭВМ. М.: Наука, 1987.
4. Макмеллан Дж. Х., Рейдер Ч. М. Применение теории чисел в цифровой обработке сигналов. М.: Радио и связь, 1983.
5. Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
6. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г.
7. Золотарев В. В. Помехоустойчивое кодирование. Методы и алгоритмы:
справочник / В. В. Золотарев, Г. В. Овечкин. – М.: Горячая линия –
Телеком, 2004. – 126 с.
8. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. М.: Мир, 1989.
9. Лидл Р., Нидеррайтер Г. Конечные поля, т.1. М.: Мир, 1988
10. Волошина В. Н., Руднева И. В. Надежное хранение информации с помощью кодов Рида-Соломона: Препр. Владивосток: ИАПУ ДВНЦ АН СССР, 1987, 13 с.
11. Волошина В. Н., Герасимов В. В., Руднева И. В., Программно-технологическая система хранения информации с повышенной надежностью: Препр. Владивосток: ИАПУ ДВО АН СССР, 1989, 22 с.
ПРИЛОЖЕНИЯ
Приложение 1.
Приложение 2
Листинг программы
Модуль программного комплекса, реализующего построение поля 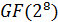, введение основных операций в этом поле, вычисление значения произвольного многочлена в любой точке поля, вычисление прямого и обратного ДПФ,ОДПФ, трехмерного преобразования Фурье и БПФ длин 255,3,5,17,15,51,85, кодирование вектора несистематическим кодом Рида-Соломона.
program GF2_8;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n=255;
n1=8;
type m = packed array [1..n1] of char;
type Gal = array [0..n] of m;
type vect= array [0..n-1] of m;
type D3vect=array [0..2] of m;
type D5vect=array [0..4] of m;
type D17vect=array [0..16] of m;
type multPol=array [0..6] of m;
type deg3Pol=array [0..3] of m;
type degBig=array [0..18] of m;
type deg15Pol=array [0..15] of m;
type D85vect=array [0..84] of m;
type D51vect=array [0..50] of m;
type D15vect=array [0..14] of m;
//-----------------------
function plus(a,b:m):m;
var i: integer;
begin
for i:=1 to 8 do
if a[i]<>b[i] then plus[i]:='1'
else plus[i]:='0';
end;
//-----------------------
function LogZ(a:m; G:Gal): integer;
var i: integer;
label 1;
begin
if a='00000000' then LogZ:=-1 else begin
for i:=0 to n-1 do
if a=G[i] then begin LogZ:=i; goto 1; end;
end;
1:end;
//------------------------
function expZ(k: integer; A:Gal): m;
begin
if k=-1 then expZ:='00000000'
else
expZ:=A[k];
end;
//-----------------------
function mult(a,b:m; G:Gal):m;
var i,j,Log: integer;
begin
i:=LogZ(a,G);
j:=LogZ(b,G);
if (i=-1)or(j=-1) then mult:='00000000'
else begin Log:=(i+j) mod 255
mult:=expZ(Log,G);
end;
end;
//-----------------------
procedure Generate(var A:Gal);
var C7: m;
i,j:integer;
c:char;
fl: boolean;
begin
A[0]:='00000001';
C7:='00011101';
fl := false;
for i:= 1 to n do
begin
c:=A[i-1,1];
if c = '1' then fl := true;
for j:=1 to 8 do
A[i,j]:=A[i-1,j+1];
A[i,8]:='0';
if fl = true then begin
for j := 1 to n1 do
if A[i, j] <> C7[j] then A[i, j] :='1' else A[i, j] := '0';
fl:=false;
end;
end;
end;
//----------------------
function powZ(a:m; i:integer; G:gal):m;
var k,t: integer;
begin
if a='00000000' then powZ:='00000000' else begin //0^a=0
k:=LogZ(a,G);
t:=k*i mod 255;
powZ:=expZ(t,G);
end;
end;
//--------------------------------------------------
function dim3FUR(c:vect;G:gal):vect;
var i,j,k,t,t1,t2,t3: integer;
A,f3,f5,f17: array[0..16,0..4,0..2] of m;
temp,su,D,DD: m; it: integer;
begin
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do begin
A[i,j,k]:=c[( 85*k+51*j+120*i) mod 255];
end;
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do begin
su:='00000000';
for t:=0 to 2 do begin
DD:=powZ(G[85],t*k,G);
temp:=mult(A[i,j,t],DD,G);
su:=plus(su,temp);
end;
f3[i,j,k]:=su;
end;
for i:=0 to 16 do
for k:=0 to 2 do
for j:=0 to 4 do begin
su:='00000000';
for t:=0 to 4 do begin
DD:=powZ(G[51],t*j,G);
temp:=mult(f3[i,t,k],DD,G);
su:=plus(su,temp);
end;
f5[i,j,k]:=su;
end;
for j:=0 to 4 do
for k:=0 to 2 do
for i:=0 to 16 do begin
su:='00000000';
for t:=0 to 16 do begin
DD:=powZ(G[120],t*i,G);
temp:=mult(f5[t,j,k],DD,G);
su:=plus(su,temp);
end;
f17[i,j,k]:=su;
end;
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do
dim3FUR[ (85*k+51*j+120*i) mod 255]:=f17[i,j,k];
end;
//-------------------------------------------------------------
function DPF256(c:vect;G:gal):vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to n-1 do begin
r:='00000000';
for i:=0 to n-1 do begin
temp:=mult(c[i],powZ(G[1],i*j,G),G);
r:=plus(temp,r);
end;
DPF256[j]:=r;
end;
end;
//-------------------------------------------------------------
function DPF256back(c:vect;G:gal):vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to n-1 do begin
r:='00000000';
for i:=0 to n-1 do begin
temp:=mult(c[i],powZ(G[254],i*j,G),G);
r:=plus(temp,r);
end;
DPF256back[j]:=r;
end;
end;
//------------------------------------------------------------------
function DPF17(c:D17vect;G:gal):d17vect
var i,j: integer;
temp,r:m;
begin
for j:=0 to 16 do begin
r:='00000000';
for i:=0 to 16 do begin
temp:=mult(c[i],powZ(G[120],i*j,G),G);
r:=plus(temp,r);
end;
DPF17[j]:=r;
end;
end;
//------------------------------------------------------------------
function DPF17back(c:D17vect;G:gal):d17vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to 16 do begin
r:='00000000';
for i:=0 to 16 do begin
temp:=mult(c[i],powZ(G[135],i*j,G),G);
r:=plus(temp,r);
end;
DPF17back[j]:=r;
end;
end;
//------------------------------------------------------------------
function DPF3(c:D3vect;G:gal):d3vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to 2 do begin
r:='00000000';
for i:=0 to 2 do begin
temp:=mult(c[i],powZ(G[85],i*j,G),G);
r:=plus(temp,r);
end;
DPF3[j]:=r;
end;
end;
//------------------------------------------------------------------
function DPF3back(c:D3vect;G:gal):d3vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to 2 do begin
r:='00000000';
for i:=0 to 2 do begin
temp:=mult(c[i],powZ(G[170],i*j,G),G);
r:=plus(temp,r);
end;
DPF3back[j]:=r;
end;
end;
//------------------------------------------------------------------
function DPF5(c:D5vect;G:gal):d5vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to 4 do begin
r:='00000000';
for i:=0 to 4 do begin
temp:=mult(c[i],powZ(G[51],i*j,G),G);
r:=plus(temp,r);
end;
DPF5[j]:=r;
end;
end;
//------------------------------------------------------------------
//------------------------------------------------------------------
function DPF5back(c:D5vect;G:gal):d5vect;
var i,j: integer;
temp,r:m;
begin
for j:=0 to 4 do begin
r:='00000000';
for i:=0 to 4 do begin
temp:=mult(c[i],powZ(G[204],i*j,G),G);
r:=plus(temp,r);
end;
DPF5back[j]:=r;
end;
end;
//------------------------------------------------------------------
function RootOfPol(pol:vect;root:m; G:gal):m;
var temp_v: vect;
sum: m;
i: integer;
begin
temp_v[0]:=pol[0];
for i:=1 to 254 do
if pol[i]<>'00000000' then
temp_v[i]:=mult(pol[i],powZ(root,i,G),G)
else temp_v[i]:='00000000';
sum:='00000000';
for i:=0 to 254 do
sum:=plus(sum,temp_v[i]);
RootOfPol:=sum;
end;
//-------------------------------------------------------------------
function RS_Encrypt(inf: vect; G:Gal):vect;
var i: integer;
begin
for i:=0 to 254 do
RS_Encrypt[i]:=RootOfPol(inf,G[255-i],G);
end;
//--------------------------------------------------------------------
procedure waste(DateTime,DateTime1:TDateTime);
var Hour,Min,Sec,Msec,Hour1,Min1,Sec1,Msec1:word;
Ms,sss:integer;
begin
decodetime(DateTime,Hour,Min,Sec,Msec); decodetime(DateTime1,Hour1,Min1,Sec1,Msec1);
ms:=Msec1-msec;
sss:=sec1-sec;
if ms<0 then begin
MS:=ms+1000;
SSS:=sss-1;
end;
writeln('algorithm waste is ',sss,' seconds, and ',ms{mod 65000},' milliseconds');
end;
//--------------------------------------------------------------------
function Dim3RPF(h:D3vect;G:Gal):D3vect;
var s1,m1,s2,tt: m;
begin
s1:=plus(h[1],h[2]);
m1:=mult(G[85],s1,G);
tt:=plus(h[0],s1);
s2:=plus(tt,m1);
Dim3RPF[1]:=plus(s2,h[1]);
Dim3RPF[2]:=plus(s2,h[2]);
Dim3RPF[0]:=tt;
end;
//--------------------------------------------------------------------
function Dim3RPFback(h:D3vect;G:Gal):D3vect;
var s1,m1,s2,tt: m;
begin
s1:=plus(h[1],h[2]);
m1:=mult(G[170],s1,G);
tt:=plus(h[0],s1);
s2:=plus(tt,m1);
Dim3RPFback[1]:=plus(s2,h[1]);
Dim3RPFback[2]:=plus(s2,h[2]);
Dim3RPFback[0]:=tt;
end;
//--------------------------------------------------------------------
function Dim5RPF(h:D5vect;G:Gal):D5vect;
var s1,s2,s3,s4,s5,m1,m2,m3,m4,m5,s6,s7,s8,s9,s10,s11,s12,tt: m;
begin
s1:=plus(h[2],h[3]);
s2:=plus(h[1],h[4]);
s3:=plus(h[1],h[3]);
s4:=plus(h[2],h[4]);
s5:=plus(s1,s2);
tt:=plus(s5,h[0]);
Dim5RPF[0]:=tt;
m1:=mult(plus(G[0],G[153]),s5,G);
m2:=mult(plus(G[153],G[204]),s1,G);
m3:=mult(plus(G[51],G[153]),s2,G);
m4:=mult(plus(G[51],G[204]),s3,G);
m5:=mult(plus(G[51],G[204]),s4,G);
s6:=plus(tt,m1);
s7:=plus(s6,m2);
s8:=plus(s6,m3);
s9:=plus(m5,h[2]);
s10:=plus(m4,h[1]);
s11:=plus(m5,h[4]);
s12:=plus(m4,h[3]);
Dim5RPF[1]:=plus(s8,s9);
Dim5RPF[2]:=plus(s7,s10);
Dim5RPF[3]:=plus(s7,s11);
Dim5RPF[4]:=plus(s8,s12);
end;
//--------------------------------------------------------------------
//--------------------------------------------------------------------
function Dim5RPFback(h:D5vect;G:Gal):D5vect;
var s1,s2,s3,s4,s5,m1,m2,m3,m4,m5,s6,s7,s8,s9,s10,s11,s12,tt: m;
begin
s1:=plus(h[2],h[3]);
s2:=plus(h[1],h[4]);
s3:=plus(h[1],h[3]);
s4:=plus(h[2],h[4]);
s5:=plus(s1,s2);
tt:=plus(s5,h[0]);
Dim5RPFback[0]:=tt;
m1:=mult(plus(G[0],G[102]),s5,G);
m2:=mult(plus(G[102],G[51]),s1,G);
m3:=mult(plus(G[204],G[102]),s2,G);
m4:=mult(plus(G[204],G[51]),s3,G);
m5:=mult(plus(G[204],G[51]),s4,G);
s6:=plus(tt,m1);
s7:=plus(s6,m2);
s8:=plus(s6,m3);
s9:=plus(m5,h[2]);
s10:=plus(m4,h[1]);
s11:=plus(m5,h[4]);
s12:=plus(m4,h[3]);
Dim5RPFback[1]:=plus(s8,s9);
Dim5RPFback[2]:=plus(s7,s10);
Dim5RPFback[3]:=plus(s7,s11);
Dim5RPFback[4]:=plus(s8,s12);
end;
//----------------------------
function multVaryOnVary(R,B:deg3Pol; G:Gal): multPol;
var s1,s2,s3,s4,s5,s6,m1,m2,m3,m4,s7,m5,m6,m7: m;
h0,h1,h2,h3,h4,h5,h6: m;
begin
s1:=plus(r[0],r[1]);
s2:=plus(r[0],r[2]); //s2:=plus(r[0],r[2]);
s3:=plus(r[1],r[3]);
s4:=plus(s2,s3);
s5:=plus(s4,s1);
h0:=mult(r[0],b[0],G);
m1:=mult(s1,plus(b[0],b[1]),G);
m2:=mult(r[1],b[1],G);
s6:=plus(h0,m2);
h1:=plus(s6,m1);
m3:=mult(r[2],b[2],G);
h6:=mult(r[3],b[3],G);
m4:=mult(s2,plus(b[0],b[2]),G);
h2:=plus(s6,plus(m3,m4));
s7:=plus(m3,h6);
m5:=mult(s3,plus(b[1],b[3]),G);
m6:=mult(s5,plus(b[2],b[3]),G);
m7:=mult(s4,plus(plus(b[0],b[1]),plus(b[2],b[3])),G);
h5:=plus(s7,m6);
h4:=plus(s7,plus(m2,m5));
h3:=plus(plus(h1,h5),plus(m4,plus(m5,m7)));
multVaryOnVary[0]:=h0;
multVaryOnVary[1]:=h1;
multVaryOnVary[2]:=h2;
multVaryOnVary[3]:=h3;
multVaryOnVary[4]:=h4;
multVaryOnVary[5]:=h5;
multVaryOnVary[6]:=h6;
end;
//--------------------------
function multFixonVary(r:deg3Pol;G:Gal):multPol;
begin
multFixonVary[0]:=plus(r[0],mult(r[0],G[85],G));
multFixonVary[1]:=plus(plus(r[0],r[1]),mult(r[1],G[85],G));
multFixonVary[2]:=plus(plus(r[1],r[2]),mult(plus(r[0],r[2]),G[85],G));
multFixonVary[3]:=plus(plus(r[0],r[2]),plus(r[3],mult(plus(r[1],r[3]),G[85],G)));
multFixonVary[4]:=plus(plus(r[1],r[3]),mult(r[2],G[85],G));
multFixonVary[5]:=plus(r[2],mult(r[3],G[85],G));
multFixonVary[6]:=r[3];
end;
//----------------------------------
function sumBigPol(H,P:degBig):degBig;
var i: integer;
begin
for i:=0 to 18 do
sumBigPol[i]:=plus(H[i],P[i]);
end;
//--------------------------
function sum3Pol(H,P:Deg3Pol):deg3Pol;
var i: integer;
begin
for i:=0 to 3 do
sum3Pol[i]:=plus(H[i],P[i]);
end;
//----------------------
function sumSmallPol(H,P:multPol):multPol;
var i: integer;
begin
for i:=0 to 6 do
sumSmallPol[i]:=plus(H[i],P[i]);
end;
//--------------------
function sum17Pol(H,P:D17Vect):D17Vect;
var i: integer;
begin
for i:=0 to 16 do
sum17Pol[i]:=plus(H[i],P[i]);
end;
//-------------------
function PxmoDD(P:DegBig): deg15Pol;
var i: integer;
begin
for i:=15 downto 3 do
PxmoDD[i]:=P[i];
PxmoDD[2]:=plus(P[2],P[18]);
PxmoDD[1]:=plus(P[1],P[17]);
PxmoDD[0]:=plus(P[0],P[16]);
end;
//---------------------
function mult15to15deg(U:deg15Pol;G:Gal):deg15pol;
var W:deg15pol; i:integer;
U1,U2,U3,U4:deg3Pol;
W1,W2,W3,W4:deg3Pol;
F1,F2,F3,F4:multPol;
Temp1,Temp3,Temp5,Temp6,Temp7,temp4:multPol;
Temp2:Deg3Pol;
temp8,temp9,temp10:multPol;
temp11,temp12,temp13,temp14,temp15,temp16:multPol;
temp17,temp18,temp19,temp20,temp21,temp22,temp23,temp24:multPol;
vec1,vec2,vec3,vec4:degBig;
FullPol: degBig;
begin
w[0]:=powZ(G[120],8,G);
w[1]:=powZ(G[120],6,G);
w[2]:=powZ(G[120],13,G);
w[3]:=powZ(G[120],14,G);
w[4]:=powZ(G[120],2,G);
w[5]:=powZ(G[120],10,G);
w[6]:=powZ(G[120],16,G);
w[7]:=powZ(G[120],12,G);
w[8]:=powZ(G[120],9,G);
w[9]:=powZ(G[120],11,G);
w[10]:=powZ(G[120],4,G);
w[11]:=powZ(G[120],3,G);
w[12]:=powZ(G[120],15,G);
w[13]:=powZ(G[120],7,G);
w[14]:=powZ(G[120],1,G);
w[15]:=powZ(G[120],5,G);
U1[0]:=U[0];
U1[1]:=U[1];
U1[2]:=U[2];
U1[3]:=U[3];
U2[0]:=U[4];
U2[1]:=U[5];
U2[2]:=U[6];
U2[3]:=U[7];
U3[0]:=U[8];
U3[1]:=U[9];
U3[2]:=U[10];
U3[3]:=U[11];
U4[0]:=U[12];
U4[1]:=U[13];
U4[2]:=U[14];
U4[3]:=U[15];
W1[0]:=W[0];
W1[1]:=W[1];
W1[2]:=W[2];
W1[3]:=W[3];
W2[0]:=W[4];
W2[1]:=W[5];
W2[2]:=W[6];
W2[3]:=W[7];
W3[0]:=W[8];
W3[1]:=W[9];
W3[2]:=W[10];
W3[3]:=W[11];
W4[0]:=W[12];
W4[1]:=W[13];
W4[2]:=W[14];
W4[3]:=W[15];
temp1:=multVaryOnVary(sum3Pol(U1,U2),sum3Pol(W1,W3),G); temp2:=sum3Pol(sum3Pol(U1,U2),sum3Pol(U3,U4));
temp3:=multVaryOnVary(temp2,W2,G);
temp4:=sumSmallPol(temp1,temp3);
temp5:=multVaryOnVary(sum3Pol(U1,U3),sum3Pol(W2,W3),G);
temp6:=multFixonVary(U2,G);
temp7:=sumSmallPol(temp4,temp5);
F1:=sumSmallPol(temp7,temp6);
temp8:=multVaryOnVary(sum3Pol(W1,W3),temp2,G);
temp9:=sumSmallPol(temp8,F1);
temp10:=multFixOnVary(sum3Pol(U2,U4),G);
F3:=sumSmallPol(temp10,temp9);
temp11:=multVaryOnVary(sum3Pol(U1,U2),sum3Pol(W1,W3),G);
temp12:=multVaryOnVary(temp2,sum3Pol(W1,sum3Pol(W2,W3)),G);
temp13:=sumSmallPol(temp11,temp12);
temp14:=multVaryOnVary(sum3Pol(U4,U2),sum3Pol(W1,W2),G);
temp15:=multFixOnVary(U3,G);
temp16:=sumSmallPol(temp14,Temp15);
F2:=sumSmallPol(temp16,temp13);
temp17:=multFixOnVary(temp2,G);
temp18:=multVaryOnVary(sum3Pol(U1,U2),sum3Pol(W1,W3),G);
temp19:=sumSmallPol(temp17,temp18);
temp20:=multVaryOnVary(temp2,W2,G);
temp21:=multVaryOnVary(sum3Pol(U2,U4),sum3Pol(W3,W4),G);
temp22:=sumSmallPol(temp21,temp20);
temp23:=sumSmallPol(temp22,temp19);
temp24:=multFixOnVary(U3,G);
F4:=sumSmallPol(temp24,temp23);
for i:=0 to 18 do begin
vec1[i]:='00000000';
vec2[i]:='00000000';
vec3[i]:='00000000';
vec4[i]:='00000000';
end;
vec1[0]:=F1[0];
vec1[1]:=F1[1];
vec1[2]:=F1[2];
vec1[3]:=F1[3];
vec1[4]:=F1[4];
vec1[5]:=F1[5];
vec1[6]:=F1[6];
//*x^4
vec2[4]:=F2[0];
vec2[5]:=F2[1];
vec2[6]:=F2[2];
vec2[7]:=F2[3];
vec2[8]:=F2[4];
vec2[9]:=F2[5];
vec2[10]:=F2[6];
//*x^8
vec3[8]:=F3[0];
vec3[9]:=F3[1];
vec3[10]:=F3[2];
vec3[11]:=F3[3];
vec3[12]:=F3[4];
vec3[13]:=F3[5];
vec3[14]:=F3[6];
//*x^12
vec4[12]:=F4[0];
vec4[13]:=F4[1];
vec4[14]:=F4[2];
vec4[15]:=F4[3];
vec4[16]:=F4[4];
vec4[17]:=F4[5];
vec4[18]:=F4[6];
FullPol:=sumBigPol(sumBigPol(vec1,vec2),sumBigPol(vec3,vec4));
mult15to15deg:=PxmoDD(FullPol);
end;
//-------------------
function mult15to15degobr(U:deg15Pol;G:Gal):deg15pol;
var W:deg15pol; i:integer;
U1,U2,U3,U4:deg3Pol;
W1,W2,W3,W4:deg3Pol;
F1,F2,F3,F4:multPol;
Temp1,Temp3,Temp5,Temp6,Temp7,temp4:multPol;
Temp2:Deg3Pol;
temp8,temp9,temp10:multPol;
temp11,temp12,temp13,temp14,temp15,temp16:multPol;
temp17,temp18,temp19,temp20,temp21,temp22,temp23,temp24:multPol;
vec1,vec2,vec3,vec4:degBig;
FullPol: degBig;
begin
w[0]:=powZ(G[135],8,G);
w[1]:=powZ(G[135],6,G);
w[2]:=powZ(G[135],13,G);
w[3]:=powZ(G[135],14,G);
w[4]:=powZ(G[135],2,G);
w[5]:=powZ(G[135],10,G);
w[6]:=powZ(G[135],16,G);
w[7]:=powZ(G[135],12,G);
w[8]:=powZ(G[135],9,G);
w[9]:=powZ(G[135],11,G);
w[10]:=powZ(G[135],4,G);
w[11]:=powZ(G[135],3,G);
w[12]:=powZ(G[135],15,G);
w[13]:=powZ(G[135],7,G);
w[14]:=powZ(G[135],1,G);
w[15]:=powZ(G[135],5,G);
U1[0]:=U[0];
U1[1]:=U[1];
U1[2]:=U[2];
U1[3]:=U[3];
U2[0]:=U[4];
U2[1]:=U[5];
U2[2]:=U[6];
U2[3]:=U[7];
U3[0]:=U[8];
U3[1]:=U[9];
U3[2]:=U[10];
U3[3]:=U[11];
U4[0]:=U[12];
U4[1]:=U[13];
U4[2]:=U[14];
U4[3]:=U[15];
W1[0]:=W[0];
W1[1]:=W[1];
W1[2]:=W[2];
W1[3]:=W[3];
W2[0]:=W[4];
W2[1]:=W[5];
W2[2]:=W[6];
W2[3]:=W[7];
W3[0]:=W[8];
W3[1]:=W[9];
W3[2]:=W[10];
W3[3]:=W[11];
W4[0]:=W[12];
W4[1]:=W[13];
W4[2]:=W[14];
W4[3]:=W[15];
temp1:=multVaryOnVary(sum3Pol(U1,U2),sum3Pol(W1,W3),G); temp2:=sum3Pol(sum3Pol(U1,U2),sum3Pol(U3,U4));
temp3:=multVaryOnVary(temp2,W2,G);
temp4:=sumSmallPol(temp1,temp3);
temp5:=multVaryOnVary(sum3Pol(U1,U3),sum3Pol(W2,W3),G);
temp6:=multFixonVary(U2,G);
temp7:=sumSmallPol(temp4,temp5);
F1:=sumSmallPol(temp7,temp6);
temp8:=multVaryOnVary(sum3Pol(W1,W3),temp2,G);
temp9:=sumSmallPol(temp8,F1);
temp10:=multFixOnVary(sum3Pol(U2,U4),G);
F3:=sumSmallPol(temp10,temp9);
temp11:=multVaryOnVary(sum3Pol(U1,U2),sum3Pol(W1,W3),G);
temp12:=multVaryOnVary(temp2,sum3Pol(W1,sum3Pol(W2,W3)),G);
temp13:=sumSmallPol(temp11,temp12);
temp14:=multVaryOnVary(sum3Pol(U4,U2),sum3Pol(W1,W2),G); temp15:=multFixOnVary(U3,G);
temp16:=sumSmallPol(temp14,Temp15);
F2:=sumSmallPol(temp16,temp13);
temp17:=multFixOnVary(temp2,G);
temp18:=multVaryOnVary(sum3Pol(U1,U2),sum3Pol(W1,W3),G);
temp19:=sumSmallPol(temp17,temp18);
temp20:=multVaryOnVary(temp2,W2,G);
temp21:=multVaryOnVary(sum3Pol(U2,U4),sum3Pol(W3,W4),G);
temp22:=sumSmallPol(temp21,temp20);
temp23:=sumSmallPol(temp22,temp19);
temp24:=multFixOnVary(U3,G);
F4:=sumSmallPol(temp24,temp23);
for i:=0 to 18 do begin
vec1[i]:='00000000';
vec2[i]:='00000000';
vec3[i]:='00000000';
vec4[i]:='00000000';
end;
//*x^0
vec1[0]:=F1[0];
vec1[1]:=F1[1];
vec1[2]:=F1[2];
vec1[3]:=F1[3];
vec1[4]:=F1[4];
vec1[5]:=F1[5];
vec1[6]:=F1[6];
//*x^4
vec2[4]:=F2[0];
vec2[5]:=F2[1];
vec2[6]:=F2[2];
vec2[7]:=F2[3];
vec2[8]:=F2[4];
vec2[9]:=F2[5];
vec2[10]:=F2[6];
//*x^8
vec3[8]:=F3[0];
vec3[9]:=F3[1];
vec3[10]:=F3[2];
vec3[11]:=F3[3];
vec3[12]:=F3[4];
vec3[13]:=F3[5];
vec3[14]:=F3[6];
//*x^12
vec4[12]:=F4[0];
vec4[13]:=F4[1];
vec4[14]:=F4[2];
vec4[15]:=F4[3];
vec4[16]:=F4[4];
vec4[17]:=F4[5];
vec4[18]:=F4[6];
FullPol:=sumBigPol(sumBigPol(vec1,vec2),sumBigPol(vec3,vec4));
mult15to15degobr:=PxmoDD(FullPol);
end;
//*****************************************************************************
function Dim17RPF(v:D17Vect; G: Gal):D17Vect;
var i: integer;
firstV: D17Vect;
secondV: deg15pol;
item: D17Vect;
res: D17Vect;
U: deg15pol;
s:m;
begin
s:='00000000';
for i:=0 to 16 do
s:=plus(s,v[i]);
FirstV[0]:=s;
for i:=1 to 16 do
FirstV[i]:=v[0];
U[0]:=v[5];
U[1]:=v[1];
U[2]:=v[7];
U[3]:=v[15];
U[4]:=v[3];
U[5]:=v[4];
U[6]:=v[11];
U[7]:=v[9];
U[8]:=v[12];
U[9]:=v[16];
U[10]:=v[10];
U[11]:=v[2];
U[12]:=v[14];
U[13]:=v[13];
U[14]:=v[6];
U[15]:=v[8];
secondV:=mult15to15deg(U,G);
item[0]:='00000000';
for i:=1 to 16 do
item[i]:=secondV[i-1];
res:=sum17Pol(item,firstV);
Dim17RPF[0]:=res[0];
Dim17RPF[5]:=res[1];
Dim17RPF[8]:=res[2];
Dim17RPF[6]:=res[3];
Dim17RPF[13]:=res[4];
Dim17RPF[14]:=res[5];
Dim17RPF[2]:=res[6];
Dim17RPF[10]:=res[7];
Dim17RPF[16]:=res[8];
Dim17RPF[12]:=res[9];
Dim17RPF[9]:=res[10];
Dim17RPF[11]:=res[11];
Dim17RPF[4]:=res[12];
Dim17RPF[3]:=res[13];
Dim17RPF[15]:=res[14];
Dim17RPF[7]:=res[15];
Dim17RPF[1]:=res[16];
end;
//*****************************************************************************
function Dim17RPFobr(v:D17Vect; G: Gal):D17Vect;
var i: integer;
firstV: D17Vect;
secondV: deg15pol;
item: D17Vect;
res: D17Vect;
U: deg15pol;
s:m;
begin
s:='00000000';
for i:=0 to 16 do
s:=plus(s,v[i]);
FirstV[0]:=s;
for i:=1 to 16 do
FirstV[i]:=v[0];
U[0]:=v[5];
U[1]:=v[1];
U[2]:=v[7];
U[3]:=v[15];
U[4]:=v[3];
U[5]:=v[4];
U[6]:=v[11];
U[7]:=v[9];
U[8]:=v[12];
U[9]:=v[16];
U[10]:=v[10];
U[11]:=v[2];
U[12]:=v[14];
U[13]:=v[13];
U[14]:=v[6];
U[15]:=v[8];
secondV:=mult15to15degobr(U,G);
item[0]:='00000000';
for i:=1 to 16 do
item[i]:=secondV[i-1];
res:=sum17Pol(item,firstV);
Dim17RPFobr[0]:=res[0];
Dim17RPFobr[5]:=res[1];
Dim17RPFobr[8]:=res[2];
Dim17RPFobr[6]:=res[3];
Dim17RPFobr[13]:=res[4];
Dim17RPFobr[14]:=res[5];
Dim17RPFobr[2]:=res[6];
Dim17RPFobr[10]:=res[7];
Dim17RPFobr[16]:=res[8];
Dim17RPFobr[12]:=res[9];
Dim17RPFobr[9]:=res[10];
Dim17RPFobr[11]:=res[11];
Dim17RPFobr[4]:=res[12];
Dim17RPFobr[3]:=res[13];
Dim17RPFobr[15]:=res[14];
Dim17RPFobr[7]:=res[15];
Dim17RPFobr[1]:=res[16];
end;
//--------------------
function RPF256(c:vect;G:Gal):vect;
var i,j,k,t: integer;
A,f3,f5,f17: array[0..16,0..4,0..2] of m;
temp:D3vect;
temp1:D5Vect;
fur2:D5vect;
fur1:D3Vect;
fur3:D17Vect;
temp2:D17Vect;
s:m;
r:integer;
begin
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do begin
A[i,j,k]:=c[( 85*k+51*j+120*i) mod 255];
end;
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do begin
temp[k]:=A[i,j,k];
if k=2 then begin
fur1:=dim3RPF(temp,G);
for t:=0 to 2 do
f3[i,j,t]:=fur1[t];
end;
end;
for i:=0 to 16 do
for k:=0 to 2 do
for j:=0 to 4 do begin
temp1[j]:=f3[i,j,k];
if j=4 then begin
fur2:=dim5RPF(temp1,G);
for t:=0 to 4 do
f5[i,t,k]:=fur2[t];
end;
end;
for j:=0 to 4 do
for k:=0 to 2 do
for i:=0 to 16 do begin
temp2[i]:=f5[i,j,k];
if i=16 then begin
fur3:=dim17RPF(temp2,G);
for t:=0 to 16 do
f17[t,j,k]:=fur3[t];
end;
end;
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do
RPF256[ (85*k+51*j+120*i) mod 255]:=f17[i,j,k];
end;
//-----------------------------------------------------------------------------
function RPF256back(c:vect;G:Gal):vect;
var i,j,k,t: integer;
A,f3,f5,f17: array[0..16,0..4,0..2] of m;
temp:D3vect;
temp1:D5Vect;
fur2:D5vect;
fur1:D3Vect;
fur3:D17Vect;
temp2:D17Vect;
s:m;
r:integer;
begin
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do begin
A[i,j,k]:=c[( 85*k+51*j+120*i) mod 255];
end;
for i:=0 to 16 do
for j:=0 to 4 do
for k:=0 to 2 do begin
temp[k]:=A[i,j,k];
if k=2 then begin
fur1:=dim3RPFback(temp,G);
for t:=0 to 2 do
f3[i,j,t]:=fur1[t];
end;
end;
for i:=0 to 16 do
for k:=0 to 2 do
for j:=0 to 4 do begin
temp1[j]:=f3[i,j,k];
if j=4 then begin
fur2:=dim5RPFback(temp1,G);
for t:=0 to 4 do
f5[i,t,k]:=fur2[t];
end;
end;
for j:=0 to 4 do
for k:=0 to 2 do
for i:=0 to 16 do begin
temp2[i]:=f5[i,j,k];